- теория по физике 🧲 молекулярная физика, МКТ, газовые законы
- Объединенный газовый закон применительно к изопроцессам
- Изотермический процесс. Закон Бойля — Мариотта.
- Изохорный процесс. Закон Шарля.
- Изобарный процесс. Закон Гей-Люссака.
- Графики изопроцессов
- Изопроцессы в газах.
- Изобарный процесс.
- Изохорный процесс.
- Изотермический процесс.
- Изоэнтропийный процесс.
- Уравнение состояния идеального газа. Изопроцессы
- 💥 Видео
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:
При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:
p V T . . = c o n s t и л и p 1 V 1 T 1 . . = p 2 V 2 T 2 .
Видео:Урок 34 (осн). Сила упругости. Закон ГукаСкачать

Объединенный газовый закон применительно к изопроцессам
Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.
Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.
Изотермический процесс. Закон Бойля — Мариотта.
Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:
Для изотермического процесса действует закон Бойля — Мариотта:
Закон Бойля — Мариотта
Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.
Изохорный процесс. Закон Шарля.
Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:
Для изохорного процесса действует закон Шарля:
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
p T . . = c o n s t ( p 1 T 1 . . = p 2 T 2 . . )
Изобарный процесс. Закон Гей-Люссака.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
V T . . = c o n s t ( V 1 T 1 . . = V 2 T 2 . . )
Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Так как газ нагревают, то:
Запишем закон Шарля применительно к данному случаю:
p T 1 . . = 1 , 6 p 240 + T 1 . .
Сделаем некоторые преобразования и вычислим начальную температуру:
p T 1 . . = 1 , 6 p 240 + T 1 . .
240 + T 1 = 1 , 6 T 1
T 1 = 240 0 , 6 . . = 400 ( К )
Подсказки к задачам на газовые законы
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
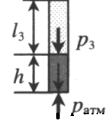 | |||||||||||||||||
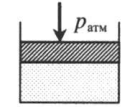
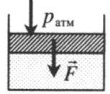
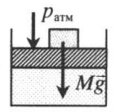
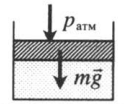
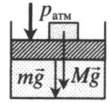
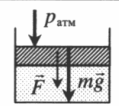
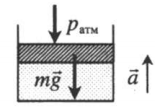
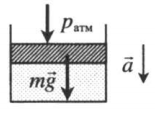
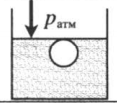
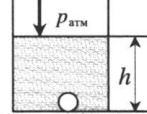
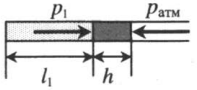
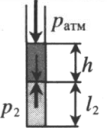
| Шар или понтон поднимается вверх в воздухе или жидкости | Архимедова сила больше силы тяжести: Пример №2. Поршень площадью 10 см 2 массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с 2 ? Изменение температуры газа не учитывать. 10 см 2 = 10 –3 м 2 100 кПа = 10 5 Па Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем: p 1 = p а т м + m g S . . Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх: p 2 = p а т м + m g S . . + m a S . . Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно: Объемы в 1 и 2 случае будут определяться формулами: h1 — расстояние от нижнего края поршня до дна сосуда в первом случае. h2 — та же самая величина, но во втором случае (искомая величина). Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов: p 1 V 1 = S h 1 ( p а т м + m g S . . ) p 2 V 2 = S h 2 ( p а т м + m g S . . + m a S . . ) Так как это изотермический процесс, правые части уравнений можно приравнять: S h 1 ( p а т м + m g S . . ) = S h 2 ( p а т м + m g S . . + m a S . . ) Видео:Задание номер 1 страница 106. Физика 7 класс.Скачать  Видео:10 класс, 46 урок, Применение производной для отыскания наибольших и наименьших значений величинСкачать  Графики изопроцессовИзопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.
|
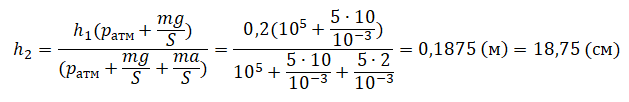
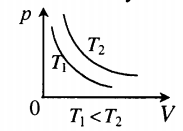
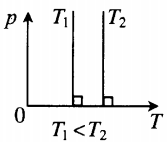
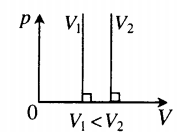
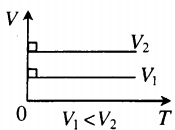
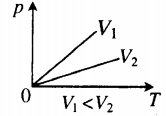
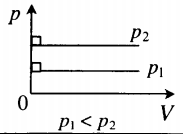
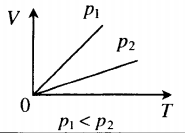

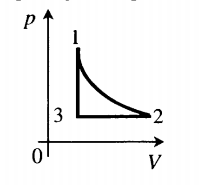
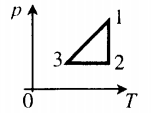
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.











![Как узнать состав образца [Про спектральный анализ в простой форме]](https://i.ytimg.com/vi/jPEbvUyjyeI/0.jpg)



