- 5. Процессы. Второй закон термодинамики.
- Энтропия. Энергия Гиббса
- Понятие энтропии
- Абсолютная энтропия веществ и изменение энтропии в процессах
- Стандартная энтропия
- Стандартная энтропия образования
- Энергия Гиббса
- Стандартная энергия Гиббса образования
- Энтальпийный, энтропийный фактор и направление процесса
- Примеры решения задач
- Задачи для самостоятельного решения
- Задание А (выбрать только один ответ из предложенных):
- 🔍 Видео
Видео:Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать

5. Процессы. Второй закон термодинамики.
Второй закон термодинамики, в отличие от первого закона термодинамики, изучает все процессы, которые протекают в природе, и эти процессы можно классифицировать следующим образом.
Процессы бывают самопроизвольные, несамопроизвольные, равновесные, неравновесные.
Самопроизвольные процессы делятся на обратимые и необратимые. Второй закон термодинамики называют законом направленности процесса в изолированной системе (закон роста S). Слово «энтропия» создано в 1865 г. Р. Ю. Э. Клаузиусом – «тропе» с греческого означает превращение. В 1909 г. профессор П. Ауербах назвал царицей всех функций внутреннюю энергию, а S – тенью этой царицы. Энтропия – мера неупорядоченности системы.
Обратимые и необратимые процессы.
Необратимые процессы идут без затраты работы, протекают самопроизвольно лишь в одном направлении, это такие изменения состояния в изолированной системе, когда при обращении процессов свойства всей системы меняются. К ним относятся:
1) теплопроводность при конечной разности температур;
2) расширение газа при конечной разности давлений;
3) диффузия при конечной разности концентраций.
Обратимыми процессами в изолированной системе называются такие процессы, которые можно обратить без каких-либо изменений в свойствах этой системы.
Обратимые: механические процессы в системе, где отсутствует трение (идеальная жидкость, ее движение, незатухающие колебания маятника в вакууме, незатухающие электромагнитные колебания и распространение электромагнитных волн там, где нет поглощения), которые могут возвратиться в начальное состояние.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, Nа с большой скоростью движется по поверхности, так как идет выделение водорода проверить.).
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – не может быть перехода тепла от менее нагретого к более нагретому телу.
2. Постулат Томсона – теплота наиболее холодного тела не может служить источником работы.
Теорема Карно – Клаузиуса: все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела.
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики.
Q2 / Т2 – приведенное тепло холодильника;
Q1 /Т1= Q2 /Т2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим.
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то.
Это четвертое уравнение второго закона термодинамики Если процесс является замкнутым, то.
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
Это шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
Это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
Действие, обратное логарифму – потенцирование:
Первый закон термодинамики определяется постоянством функции U в изолированной системе. Найдем функцию, выражающую содержание второго закона, а именно, одностороннюю направленность протекающих в изолированной системе процессов. Изменение искомой функции должно иметь для всех реальных, т. е. необратимых процессов, протекающих в изолированных системах, один и тот же знак. Второй закон термодинамики в приложении к некруговым необратимым процессам должен выражатся неравенством. Вспомним Цикл Карно. Так как любой цикл можно заменить бесконечно большим числом бесконечно малых циклов Карно, то выражение:
Справедливо для любого обратимого цикла. Считая на каждом элементарном участке теплообмена Т = соnst, найдем, что:
И для всего цикла.
Энергия Гельмгольца Изохорно-изотермический потенциал.
Величина (V – ТS) является свойством системы; она называется энергией Гельмгольца. Была введена Гельмгольцем в 1882 г.
dF = dU – ТdS – SdТ,
dF = ТdS – рdV – SdТ,
F – полный дифференциал.
Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.
Физический смысл изохорно-изотермического потенциала.
Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: АFТ г 0. Для равновесного процесса: ΔFТ,V = 0.
Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).
Где 1 – самопроизвольный процесс;
2 – несамопроизвольный процесс;
3 – равновесный процесс.
Изобарно-изотермический потенциал.
1) G (Р, Т= соnst), энергия Гиббса.
G = U – ТS + РV = Н – ТS = F + РV,
Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;
2) функция – полный дифференциал, однозначна, конечна, непрерывна.
dG = dU – ТdS – SdТ + рdv + vdр,
dG = ТdS – рdV – ТdS – SdТ + рdv + vdр,
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;
3) G как критерий направленности процесса в изолированной системе.
Для самопроизвольного процесса: (ΔG)Р,Т 0. Для равновесного процесса: (ΔG)Р,Т = 0.
Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.
Где 1 – самопроизвольный процесс;
2 – равновесный процесс;
3 – несамопроизвольный процесс.
Совершается работа за счет ΔU и ΔН.
Противодействующие факторы. Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.
Энтальпия – Н Внутренняя энергия – U.
dН = dU + рdv + vdр,
dU = ТdS – SdТ + рdV + Vdр,
dН = –рdV + рdV + Vdр; U = ТdS + VdР.
Где 1 – самопроизвольный процесс,
2 – несамопроизвольный процесс,
3 – равновесный процесс,
Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.
Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса.
Уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).

Уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).
Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.
Уравнение Клаузиуса-Клапейрона.
Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии.
Предположим, что 1 моль вещества переходит из первой фазы во вторую.
Нет условного равновесия,
Где dР/dТ – температурный коэффициент давления,
Где λфп – теплота фазового перехода.
Уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.
Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.
Эмпирическая форма уравнения Клаузиуса-Клапейрона.
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.
I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.
II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.
Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.
Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).
Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Ти других свойств.
Итак, энтропия выражается уравнением:
Где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.
При независимых переменных U (внутренняя энергия) может обозначаться UВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:
1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;
2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, ni;
3) внутренняя энергия при независимых переменных: S, V, ni;
4) энтальпия при независимых переменных: S, Р, пi;
5) энтропия при независимых переменных Н, Р, ni..
В изолированных системах (U и V= соnst) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.
Связь энтропии с другими термодинамическими параметрами.
Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = δQ/Т в сочетании с δQ = dU + РdV и δQ = dН – VdР дает уравнения:
Применительно к функциональной зависимости φ(Т, V, S) = 0, получим.
Теперь найдем зависимость энтропии от температуры из уравнений:
Вот эти зависимости:
Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:
Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому телу».
2. Постулат Томсона – «Теплота наиболее холодного тела не может служить источником работы».
Теорема Карно-Клаузиуса: «Все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела».
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики.
Где Q /Т – приведенное тепло;
Q2 / Т2 – приведенное тепло холодильника;
Q1 /Т1= Q2 / Т2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим.
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то.
Это четвертое уравнение второго закона термодинамики.
Если процесс является замкнутым, то.
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
Шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
Это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
Термодинамическая вероятность.
Это формула Больцмана,
Где S – энтропия – степень разупорядоченности системы;
к– постоянная Больцмана;
W – термодинамическая вероятность системы макросостояний.
Термодинамическая вероятность – число микросостояний данной системы, с помощью которых можно реализовать данное макросостояние системы (Р, Т, V).
Если W = 1, то S = 0, при температуре абсолютного нуля –273°С все виды движений прекращаются.
Термодинамическая вероятность – это число способов, которыми атомы и молекулы можно распределить в объеме.
Видео:Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Энтропия. Энергия Гиббса
Понятие энтропии
Абсолютная энтропия веществ и изменение энтропии в процессах
Стандартная энтропия
Стандартная энтропия образования
Энергия Гиббса
Стандартная энергия Гиббса образования
Энтальпийный, энтропийный фактор и направление процесса
Примеры решения задач
Задачи для самостоятельного решения
Видео:Свободная энергия Гиббса. 10 класс.Скачать

Понятие энтропии
Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).
Видео:Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Абсолютная энтропия веществ и изменение энтропии в процессах
При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.
Изменение энтропии в процессе выражается уравнением:
где S(прод.) и S(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.
На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δnг. Так, для реакции
(Δnг = 1) ΔV > 0, значит, ΔS > 0.
Видео:Энергия Гиббса. Практическая часть. 10 класс.Скачать

Стандартная энтропия
Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25 о С). Энтропия в этом случае обозначается S о 298 и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S о ) увеличивается при повышении температуры.
Видео:Энтропия. 10 класс.Скачать

Стандартная энтропия образования
Стандартная энтропия образования ΔS о f,298 (или ΔS о обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.
Видео:Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Энергия Гиббса
Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:
Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.
Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG
Видео:Решение задач на вычисление энергии Гиббса. 1 часть. 10 класс.Скачать

Стандартная энергия Гиббса образования
Стандартная энергия Гиббса образования δG о f,298 (или δG о обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.
Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG о f,298 = 0.
Видео:Решение задач на вычисление энергии Гиббса. 2 часть. 10 класс.Скачать
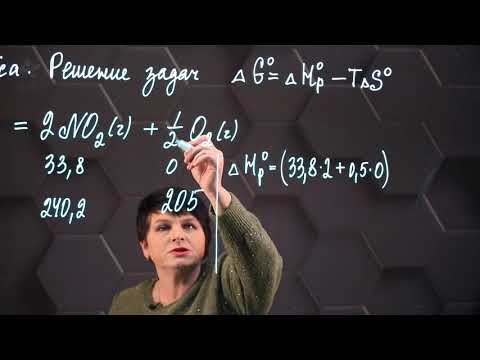
Энтальпийный, энтропийный фактор и направление процесса
Проанализируем уравнение ΔG о Т = ΔН о Т — ΔТS о Т. При низких температурах ТΔS о Т мало. Поэтому знак ΔG о Т определяется в основном значением ΔН о Т (энтальпийный фактор). При высоких температурах ТΔS о Т – большая величина, знак Δ G о Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН о Т) и энтропийного (ТΔS о Т) факторов существует четыре варианта процессов.
- Если ΔН о Т о Т > 0, то ΔG о Т
- Если ΔН о Т > 0, ΔS о Т о Т > 0 всегда (процесс не протекает ни при какой температуре).
- Если ΔН о Т о Т о Т о /ΔS о (процесс идет при низкой температуре за счет энтальпийного фактора).
- Если ΔН о Т > 0, ΔS о Т > 0, то ΔG о Т ΔН о / ΔS о (процесс идет при высокой температуре за счет энтропийного фактора).
Видео:Закон Гесса. 10 класс.Скачать

Примеры решения задач
Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:
Объяснить знак и величину ΔS о .
Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | NH3(г) | O2(г) | NО(г) | H2O(ж) |
| S о 298, Дж/(моль·К) | 192,66 | 205,04 | 210,64 | 69,95 |
В данной реакции ΔV o х.р.,298
Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH4NO3(к). Отличается ли стандартная энтропия образования NH4NO3(к) от стандартной энтропии этого соединения?
Решение. Стандартной энтропии образования NH4NO3 отвечает изменение энтропии в процессе:
Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | N2(г) | H2(г) | O2(г) | NH4NO3(к) |
| S о 298, Дж/(моль·К) | 191,50 | 130,52 | 205,04 | 151,04 |
Стандартная энтропия образования NH4NO3(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S о 298(NH4NO3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S о 298 всегда больше нуля, в то время как величины ΔS 0 f,298, как правило, знакопеременны.
Задача 3. Изменение энергии Гиббса реакции:
равно δG о 298= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.
Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS о о 298 реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS о
Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:
Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.
Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | С4Н10(г) | С2Н4(г) | Н2(г) |
| ΔG о f,298× , кДж/моль | — 17,19 | 68,14 | 0 |
| S о 298, Дж/(моль·К) | 310,12 | 219,45 | 130,52 |
ΔG о х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.
Поскольку ΔS о х.р.,298 > 0, то при температуре Т>ΔН о /ΔS о величина ΔG о х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.
Задача 5. Пользуясь справочными данными по ΔG о f,298 и S о 298, определите ΔH о 298 реакции:
Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | N2O(г) | H2(г) | N2H4(г) | H2O(ж) |
| ΔG о f,298, кДж/моль | 104,12 | 0 | 159,10 | -237,23 |
| S о 298, Дж/(моль·К) | 219,83 | 130,52 | 238,50 | 69,95 |
ΔG о 298 = ΔН о 298 – ТΔS о 298. Подставляя в это уравнение величины ΔН о 298 и ТΔS о 298, получаем:
ΔН о 298 = –182,25× 10 3 + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.
Следует подчеркнуть, что поскольку ΔS о 298 выражена в Дж/(моль× К), то при проведении расчетов ΔG 0 298 необходимо также выразить в Дж или величину ΔS 0 298 представить в кДж/(мольK).
Видео:Лекция №8 "Эффект Джоуля-Томсона. Элементы теории вероятностей"Скачать

Задачи для самостоятельного решения
1. Используя справочные данные, определите стандартную энтропию образования ΔS о f,298 NaHCO3(к).
2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO2(г):
Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Задание А (выбрать только один ответ из предложенных):
А1. Какая из данных термодинамических величин является параметром процесса, а не параметром состояния?
1) энергия Гиббса 2) энергия Гельмгольца 3) теплота 4) давление
А2. Какая из данных термодинамических величин не является функцией состояния системы?
1) энтропия 2) внутренняя энергия 3) энтальпия 4) работа
А3. Какой из процессов с участием идеального газа протекает без теплообмена с окружающей средой?
1) изобарный 2) изохорный 3) изотермический 4) адиабатический
А4. Зависимость константы равновесия химической реакции от Т дается уравнениями
1) Вант-Гоффа 2) Кирхгофа 3) Гиббса-Гельмгольца 4) Клапейрона-Клаузиуса
А5. Процессы, которые не могут протекать сами собой, без воздействия извне, удаляющие систему от равновесия, называются:
1) положительными 2) отрицательными 3) равновесными 4) обратимыми
А6. Какая термодинамическая функция является критерием достижения равновесия (критерием самопроизвольного протекания процесса) в условиях постоянства объема и энтропии?
1) внутренняя энергия 2) энергия Гиббса 3) энтальпия 4) энергия Гельмгольца
А7. Изобарно-изотермическим потенциалом является:
1) энергия Гиббса 2) энергия Гельмгольца 3) энтальпия 4) внутренняя энергия
А8. Какая из данных термодинамических величин является экстенсивным параметром состояния системы?
1) температура 2) давление 3) плотность вещества 4) энтропия
А9. Какое из данных выражений, определяющих энергию Гиббса, является неправильным?
1) G = U – TS + PV 2) G = U – TS 3) G = F + PV 4) G = Н– TS
А10. Какую термодинамическую функцию можно представить как сумму свободной и связанной энергии?
1) энтропию 2) энтальпию 3) внутреннюю энергию 4) энергию Гиббса
А11. Функцией каких переменных является энергия Гельмгольца?
1) P и T 2) V и T 3) P и S 4) V и S
А12. Выражение для химического потенциала компонента идеальной газовой смеси имеет вид:
1) mi = mio (T) + RT ln аi 2) mi = Gi¢¢(T,P) + RT ln Ni 3) mi = mi (T) + RT ln fi 4) mi = mio (T) + RT ln Ni
А13. Понижение давления пара растворителя над раствором пропорционально концентрации растворенного вещества, выраженной как
1) молярность 2) моляльность 3) нормальность 4) мольная доля
А14. Мерой влияния диссоциации (ассоциации) растворенного вещества на коллигативные свойства растворов является:
1) криоскопическая 2) 3) химическая 4) изотонический
постоянная эбуллиоскопическая постоянная переменная коэффициент
А15. Равновесие жидкость – пар в бинарных системах подчиняется:
1) законам Коновалова 2) закону Рауля 3) закону действующих масс 4) правилу рычага
А16. Возможность вычислить абсолютное значение энтропии индивидуального вещества дает:
1) тепловой закон Нернста 2) уравнение изобары (изохоры) Вант-Гоффа 3) постулат Планка 4) правило фаз Гиббса
А17. Двойному равновесию твердая фаза – пар (газ) на диаграмме состояния однокомпонентной системы (в координатах Р-Т) отвечает кривая:
1) кипения 2) возгонки 3) плавления 4) давления пара над переохлажденной жидкостью
А18. Точка на диаграмме состояния двухкомпонентной системы (в координатах температура – состав), в которой могут находиться в равновесии три фазы (расплав и два вида кристаллов), называется:
1) тройной 2) критической 3) эвтектической 4) фигуративной
А19. Максимально возможное число равновесных фаз в однокомпонентной системе равно:
1) 1 2) 2 3) 3 4) 4
А20. Число степеней свободы в точке, лежащей на кривой возгонки диаграммы однокомпонентной системы (в координатах Р-Т), равно:
1) 0 2) 1 3) 2 4) 3
Задание В (записать ответ: число, формулу, уравнение …)
В1. Чему равна теплоемкость Ср двухатомного идеального газа?
В2. Напишите выражение, передающее связь между Qp и Qv для химической реакции.
В3. Напишите выражения, определяющие изменение энтальпии в изобарном и изобарно-изотермическом процессах с участием идеального газа.
В4. Какая теплота в термохимии считается положительной: та, которую система поглощает, или та, которую система выделяет?
В5. В каких единицах измеряется теплоемкость?
В6. Напишите выражение для расчета DS в процессе, связанном с изменением T, P, V (общий случай).
В7. Напишите выражение, определяющее изохорно-изотермический потенциал.
В8. Запишите выражение для КПД цикла Карно.
В9. Напишите закон Рауля.
В10. Запишите уравнение изохоры Вант-Гоффа.
Задание С (дать ответ на вопрос)
С1. Что называется стандартной теплотой образования вещества? Как рассчитать тепловой эффект химической реакции с помощью стандартных теплот образования?
С2. Сформулировать постулат Томсона.
С3. Записать уравнения Гиббса-Гельмгольца. Какую связь дают эти уравнения?
С4. Какие переходы называются фазовыми переходами первого рода? Приведите примеры, запишите уравнение, приложимое ко всем фазовым переходам первого рода.
🔍 Видео
5.1. Адсорбция. Классификация адсорбцииСкачать

Урок 197. Поверхностная энергия. Коэффициент поверхностного натяженияСкачать

Три давления? Нет, три энергии!Скачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Консультация к устному экзамену. Механика. Часть 1: "Движение материальной точки"Скачать

Почему энергия Гиббса так важна ?Скачать

Теория к термодинамическим расчётамСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать








































