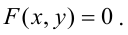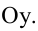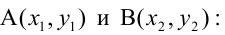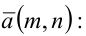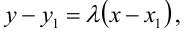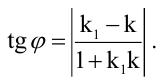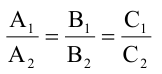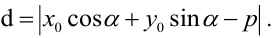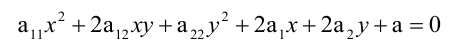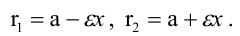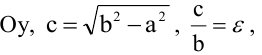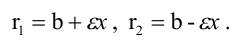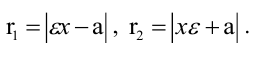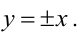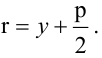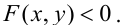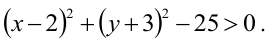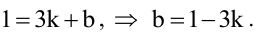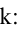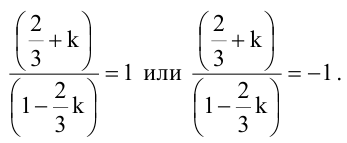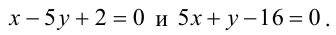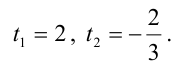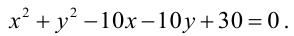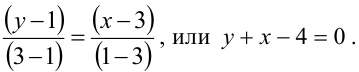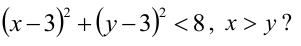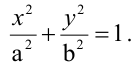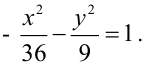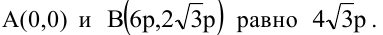Содержание:
Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 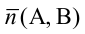
2. Уравнение прямой с угловым коэффициентом:
где 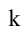
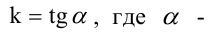
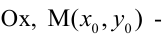
Уравнение (2.2) принимает вид 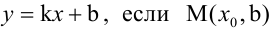
3. Уравнение прямой в отрезках:
где а и b — величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки —
5. Уравнение прямой, проходящей через данную точку 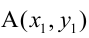
6. Нормальное уравнение прямой:
где 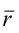
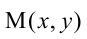
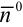
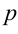
Нормальное уравнение прямой в координатной форме имеет вид:
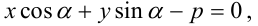
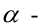
Уравнение пучка прямых с центром в точке 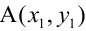
где 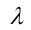
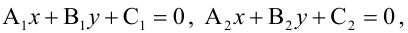
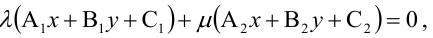
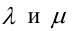
Величина угла между прямыми 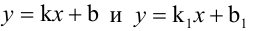
Равенство 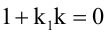
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 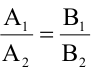
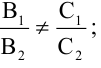
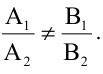
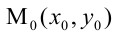
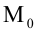
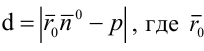
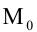
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 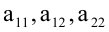
Уравнение окружности с центром в точке 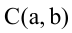

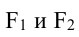
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 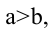
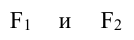
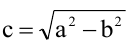
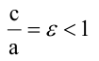
Расстояния от точки 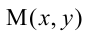
Если же 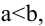
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 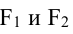
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 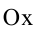
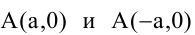
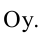
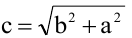
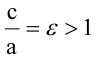
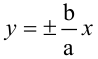
Расстояния от точки 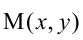
Гипербола, у которой а=b, называется равносторонней, ее уравнение 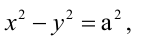
Гиперболы 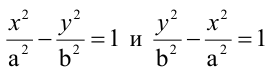
Каноническое уравнение параболы имеет два вида:
1. 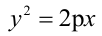
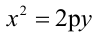
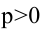
Парабола, уравнение которой 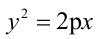
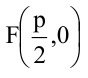
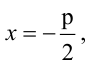
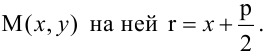
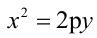
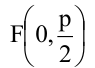
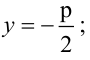
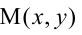
Уравнение 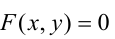
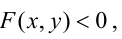
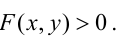
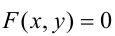
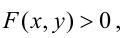
Прямая, уравнение которой 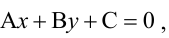
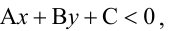
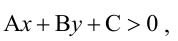
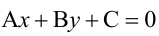
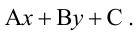
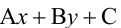
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 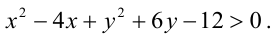
Уравнение 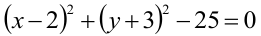
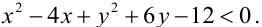
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 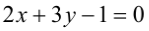
Решение:
Будем искать уравнение прямой в виде 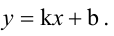
Величина угла между прямыми 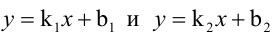
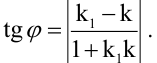
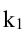
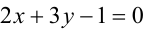
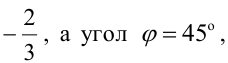
Имеем два значения 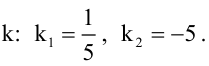
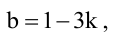
Пример:
При каком значении параметра t прямые, уравнения которых 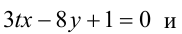
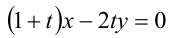
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 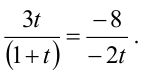
Пример:
Найти уравнение общей хорды двух окружностей: 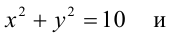
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 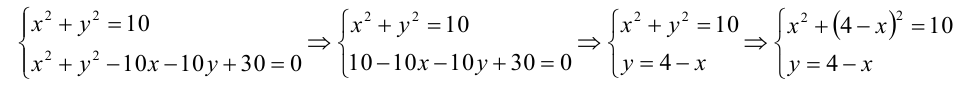
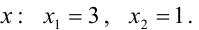
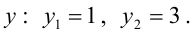
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 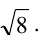
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 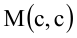
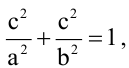
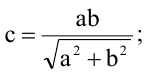
Пример:
Зная уравнение асимптот гиперболы 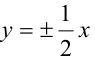
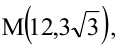
Решение:
Запишем каноническое уравнение гиперболы: 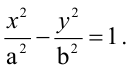
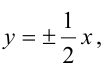
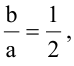
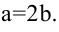
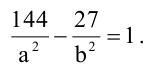
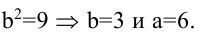
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 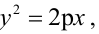
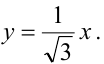
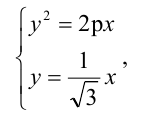
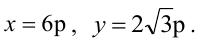
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Уравнение кривой и поверхности

есть уравнение кривой g в неявном виде, если координаты любой точки MÎ g удовлетворяют (1), и обратно, каждая
пара (x, y) чисел, удовлетворяющих (1), задает точку M(x, y) на кривой.
Подчеркнем, что при составлении уравнений следствие обязательно надо проверять в обе стороны.

задает на плоскости пару прямых (см.чертеж). Координаты любой точки A(x, y)Î l1 удовлетворяют (*), но нельзя
сказать, что (*) есть уравнение l1 , поскольку есть еще точки, координаты которых удовлетворяют (*), но на l1 эти точки не лежат.
С другой стороны, каждая точка, координаты которой удовлетворяют уравнению

лежит на фигуре l1U l2 , но нельзя сказать что (**) задает эту фигуру, поскольку есть еще точки на l1U l2, координаты которых (**) не удовлетворяют.
Пример 2. Составим уравнение окружности g радиуса R с центром в точке O¢(a, b). Пусть M(x, y) – произвольная точка окружности g . Тогда
Обратно, если координаты точки M(x, y) удовлетворяют (2), то ½O¢M½= R, а значит, MÎg. Таким образом (2) и есть уравнение нашей окружности.
Если из уравнения (1) удается выразить одну координату через другую, то получим уравнение в явном виде:
Не всегда удается привести неявное уравнение кривой к явному виду. В каком случае это возможно гласит теорема о неявной функции, изучаемая в курсе математического анализа. Например, с уравнением окружности это сделать нельзя.
Предположим, что точка движется по кривой. Тогда ее координаты изменяются со временем:

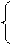
При этом параметр t изменяется в определенных пределах: tÎI, где I – интервал числовой прямой. Говорим, что (4) есть параметрические уравнения кривой g, если точка M(x, y) лежит на кривой g тогда и только тогда, когда найдется такое tÎI, что будут выполнены оба равенства (4) одновременно. При этом, обязательно к системе (4) надо добавлять интервал изменения параметра. Физический смысл параметра в (4) не всегда время.



y = R·cos a , aÎR .
Не важно, что для одной и той же точки
может найтись несколько (или даже
бесконечно много) соответствующих ей
значений параметра. Это не запрещается.
Пример 3.Уравнения


задают полукубическую параболу. Уравнения



Определение. Пусть F – некоторая поверхность в пространстве, а F(x, y, z) – функция от трех переменных. Говорим, что
есть уравнение поверхности F в неявном виде, если координаты любой точки MÎF удовлетворяют (6), и обратно, каждая пара (x, y) чисел, удовлетворяющих (6), задает точку M(x, y, z) на поверхности.
Так же, как и для кривой, при составлении уравнения поверхности, необходимо проверять следствие в обе стороны.
Упражнение. Самостоятельно докажите, что сфера радиуса R с центром в точке O¢(a, b, с) задается уравнением
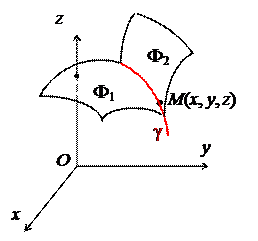
Кривая в пространстве одним уравнением, как правило, не задается. Бывают исключительные случаи, типа уравнения x 2 + y 2 = 0, которое задает прямую – ось Oz. Кривая в пространстве обычно задается системой из двух уравнений


Каждое из уравнений в отдельности задает поверхность. Если координаты
точки удовлетворяют системе, то она лежит на двух поверхностях одновременно, т.е. MÎF1IF2. Таким образом, система (8) задает линию пересечения двух поверхностей (хотя заметим, что не всегда это пересечение будет кривой). Аналогично, если мы хотим найти точки пересечения любых двух множеств, заданных своими уравнениями, мы должны объединить данные уравнения в одну систему.
Пример 4. Система уравнений


задает окружность в плоскости Oxy. Первое уравнение системы задает сферу с центром в начале координат, а второе – плоскость Oxy. Их пересечение есть окружность g. Если подставить z = 0 в первое уравнение, то получим
Казалось бы, можно сказать, что это и есть уравнение окружности g. Но это не так. Уравнение (**** )
задает цилиндрическую поверхность (см. параграф «цилиндрические и конические поверхности»). Подставляя z = 0 в первое уравнение системы, нельзя отбрасывать при этом само уравнение z = 0.
Также кривая в пространстве может быть задана параметрическими уравнениями вида

где I – интервал числовой прямой. С параметрическими уравнениями поверхности мы встретимся в разделе «Дифференциальная геометрия».
Обозначим – радиус-вектор произвольной точки M(x, y, z) на кривой, т.е. вектор с координатами, составленными из неизвестных (x, y, z), а – вектор с координатами (j( t ), y( t ), s( t )). Тогда параметрические уравнения кривой можно переписать в виде одного векторного уравнения
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнения кривых.
В аналитической геометрии всякому уравнению вида F(x; у) = 0 может соответствовать некоторая линия, свойства которой определяются данным уравнением.
Под F(x; у) = 0 понимаем многочлен степени n; степень многочлена n – порядок линии.
Значит, кривая первого порядка, в декартовой системе координат, описывается алгебраическим уравнением первого порядка ax + by + c = 0, где хотя бы один из коэффициентов a или b отличен от нуля. Это уравнение называют также линейным уравнением. А само выражение, типа ax+by+c=0 и a 2 +b 2 ≠ 0, принято обозначать как общее уравнение прямой.
Следовательно, любая прямая на плоскости представляет собой алгебраическую кривую первого порядка и любая алгебраическая кривая первого порядка на плоскости есть прямая.
Общее уравнение кривой второго порядка в декартовых координатах имеет вид:
причем, в зависимости от значения произведение аb получаем:
— эллипс, частный случай — окружность ( когда ab > 0);
📺 Видео
Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Дифференцирование. Запись уравнения касательной к кривой. Урок 6Скачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнения касательной и нормали к кривойСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Как составить уравнение касательной и нормали к графику функцииСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Видеоурок "Гипербола"Скачать

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать