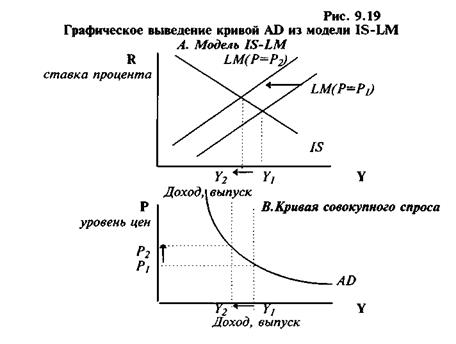
Как вывести уравнение кривой is (4 видео)

Содержание

Использование модели IS-LM для вывода функции совокупного спроса (AD).
EREPORT.RU
мировая экономика
Модель IS-LM. Особенности построения кривых IS и LM
Кривая IS
Кривая LМ
Кривая IS. Ее выведение и значение.
📹 Видео

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Использование модели IS-LM для вывода функции совокупного спроса (AD).

Равновесие модели IS-LM позволяет определить не только равновесную ставку процента и доход, но и эффективный спрос.

Эффективный спрос – это величина совокупного спроса, которая соответствует совместному равновесию на рынках товаров и денег.

Первоначальное равновесие модели IS–LM находится в точке E1(i1;Y1). Эту точку можно спроецировать на кривую AD, как точку А. Объем совокупного спроса Y1 установится при уровне цен в экономике P1. Если уровень цен возрастет до P2, то реальное количество денег уменьшится
(LM1 → LM2). Новое совместное равновесие модели IS–LM установится
в точке E2(i2;Y2). Следовательно при уровне цен P2 объем эффективного спроса составит Y2(точка В). Если уровень цен снизится до Y3, то реальное количество денег возрастет и кривая LM сместится вправо (LM1 → LM3). Новое совместное равновесие установится в точке E3(i3;Y3). При уровне цен P3 объем эффективного спроса составит Y3(точка С). Соединив точки А, В и С – получаем функцию совокупного спроса AD.

Кривая IS не изменит своего положения.

Кривая AD отражает обратную зависимость между уровнем цен
и объёмом покупок товаров и услуг. Она имеет убывающий характер (более низким ценам соответствует большее количество денежных остатков
и соответственно более высокий совокупный спрос).

Рис. 3.3 Графическое выведение кривой AD

Таблица 3.1 Исходные данные

Показатели	Значение (млрд. руб.)
Функция инвестиций I	40-2i
Номинальное предложение денег M_S
Значение дефлятора (уровень цен)
Реальный спрос на деньги MD/P	0.2Y-4i
Изменение государственных расходов ΔG
Чистый экспорт(Хn)	100-80е
Мировая ставка процента

1. Выведите уравнение кривой IS аналитически и графически.

Равновесие: AD = AS,

AS = Y, AD = Y = C + I + G (2.6)

Y = 90 + 0,8(Y – 40 – 0,1Y + 30) + 30 + 60 – 2,5i;

Y = 90 + 0,8Y – 32 – 0,08Y + 40+50+60 – 2,5i;

Y = 742,857 – 8,93i – уравнение кривой IS.

Рисунок 3.4 Кривая IS

2. Выведите уравнение кривой LM аналитически и графически.

Y = 500 + 25i – уравнение кривой LM.

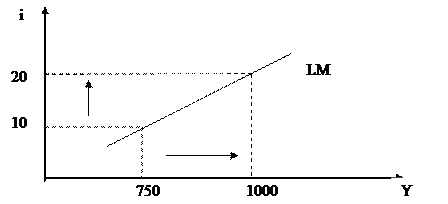Рисунок 3.5 Кривая LM

3. Найдите равновесный уровень ВВП и равновесную ставку процента, при которой достигается совместное равновесие товарного и денежного рынков. Покажите графически.

Равновесие означает, что денежное предложение достаточно для такой ставки процента, при которой инвестиции равны сбережениям.

Так как имеем уравнение кривой IS и уравнение кривой LM:

Y = 742,857 – 8,93i; Y = 500 + 25i, следовательно, можно найти равновесную ставку процента и равновесный уровень дохода:

742,857 –8,93i = 500 + 25i;

= 7,158% – равновесная ставка процента.

Подставим найденное значение ставки процента в любое из уравнений кривых: 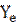= 500 + 25∙ 7,158 = 678,95(млрд. руб.) – равновесный уровень дохода.

Представим ситуацию графически:

7.158

678.95

Рисунок 3.6 Равновесие в модели IS – LM

4. Выведите уравнение кривой совокупного спроса AD. Изобразите
на графике.

Для вывода уравнения кривой AD используем уравнение кривой LM,
не подставляя в него конкретное значение реального денежного спроса
и значение общего уровня цен:

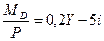
Решим это уравнение относительно Y:

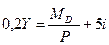
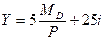
Далее решаем основное макроэкономическое тождество, подставив в него функции потребления и инвестиций, но не подставляя величину государственных расходов G:

Y = 90 + 0,8 ∙ (Y – 40 – 0,1Y + 50) + 50 – 2,5i + G,

Y=90+0,8Y – 32 – 0,08Y+40+50 – 2,5i+G

Подставляем это выражение в уравнение кривой LM и решаем относительно Y:

– уравнение кривой AD.

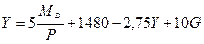
3.2 Макроэкономическая политика в модели IS – LM

Изменения на рынке благ происходят вследствие одного из компонентов совокупных расходов и выражаются в сдвиге кривой IS.

Процесс приспособления модели IS-LM к новому совместному равновесию будет происходить через «эффект вытеснения».

Рост государственных расходов (или любого другого компонента совокупного спроса) приведет к увеличению совокупного спроса с эффектом мультипликатора и кривая IS сместиться вправо(IS→IS₁). На рынке благ установится новое равновесие в точке Е₃(а не в точке Е₂), т.к. при уровне дохода Y₂ на денежном рынке возникнет дефицит (точка Е₂ лежит ниже кривой LM). Вследствие дефицита денег возрастёт спрос на них. Начнётся продажа ценных бумаг, их курсовая стоимость снизится, что приведет к росту ставки процента (i₁→i₂). Рост ставки процента приводит к уменьшению объёма инвестиций и равновесие переходит в новое состояние, в результате чего происходит уменьшение равновесного дохода (Y₂→Y₃), при более высокой ставке процента. Новое равновесие установится в точке Е₃(i₂;Y₃).

Таким образом, модель IS – LM показывает, что рост государственных расходов вызывает как увеличение выпуска с Y₁ до Y₃, так и рост процентной ставки с i₁ до i₂. Вместе с тем выпуск увеличивается в меньшей степени,
чем следовало ожидать, т. к. рост процентной ставки уменьшает мультипликационный эффект государственных расходов: прирост государственных расходов (как и увеличение других автономных расходов, снижение налогов) частично вытесняет планируемые частные инвестиции. Такое явление получило название «эффекта вытеснения».

Предположим, что государственные расходы увеличились на ∆G.

Что и в каком объеме должен предпринять Центральный банк, чтобы нейтрализовать «эффект вытеснения»?

Найдём уравнение кривой IS₁:

AD = AS, AS = Y, AD = Y = C + I + G,

Y = 90 + 0,8 ∙ (Y – 40 – 0,1Y + 50) + 50 – 2,5i + 60+60,

0,28Y = 268 – 2,5i,

Y = 957,142 – 8,93i – уравнение кривой IS_1.

Т.к. кривая LM осталась на прежнем месте и её уравнение осталось прежним Y = 500 + 25i, то найдём новую равновесную ставку процента
и равновесный уровень дохода (IS₁ = LM):

957,142 – 8,93i = 500 + 25i,

i₁= 13,47% – новая равновесная ставка процента.

Y₁ =500 + 25∙ 13,47 = 836,75 – новый равновесный уровень дохода.

Найдём «эффект вытеснения», используя формулу ∆Y = ∆G ∙ m:

m = ,

∆Y = 60 ∙ 3,57 = 214,2,

Y₂ = Y_е + ∆Y = 678,95+ 214,2 = 893,15 (млрд. руб.)

Таким образом, «эффект вытеснения» будет следующим:

ЭВ = Y₂ – Y₁ = 893,15 – 836,75 = 56,4 (млрд. руб.)

Чтобы нейтрализовать «эффект вытеснения», Центральный банк должен увеличить денежное предложение на величину ∆М (млрд. руб.), равную:

M D = (0,2Y – 5i) ∙ P,

100 + ∆M =(0,2 ∙ 893,15 – 5 ∙ 7,158) ∙1,

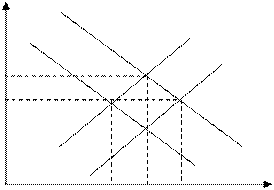Рисунок 3.9 IS-LM

Вывод: в данном разделе мы вывели уравнение кривых IS и LM:
Y = 742,857 – 8,93i и Y = 500 + 25i, соответственно. Для полученных кривых вычислили равновесную ставку процента i = 7,158 % и равновесный уровень дохода Y = 678,95 млрд. руб., то есть совместное равновесие. После чего было выведено уравнение кривой совокупного спроса .

Также мы увидели, что при увеличении государственных расходов на величину ∆G = 60 млрд. руб. возник «эффект вытеснения», и сделали вывод: чтобы его нейтрализовать, Центральный Банк должен увеличить денежное предложение на 42,84 млрд. руб.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

EREPORT.RU

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

мировая экономика

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Модель IS-LM. Особенности построения кривых IS и LM

Автор — Матвеева Татьяна Юрьевна, преподаватель НИУ-ВШЭ
«Макроэкономика: Курс лекций для экономистов», 2001 год

Кривая IS

Основой для построения кривой IS служат: 1) модель совокупных расходов (модель «Кейнсианского креста»), рассмотренная в главе 12, которая показывает, что определяет доход в экономике при данном уровне планируемых расходов (т.е. исходит из предпосылки, что уровень планируемых автономных расходов фиксирован); 2) функция зависимости автономных планируемых расходов от ставки процента.

Поскольку в модель включена новая эндогенная переменная — ставка процента — рассмотрим ее более подробно. Ставка процента и автономные расходы. Для сберегателей ставка процента выступает как вознаграждение за воздержание от потребления в настоящем в счет ожидаемого потребления в будущем. Для заемщиков ставка процента представляет собой цену заемных средств, используемых инвесторами для покупки инвестиционных товаров, а домохозяйствами для покупки потребительских товаров длительного пользования. В экономике существует множество конкретных видов процентных ставок, такие как процентные ставки, выплачиваемые:

банками по чековым, сберегательным и срочным счетам;
по средствам, занимаемым правительством (проценты по государственным облигациям),
бизнесом (проценты по коммерческим ценным бумагам и облигациям корпораций),
коммерческими банками центральному банку (учетная ставка процента),
домохозяйствами (проценты по закладным, итотечному и потребительскому кредиту).

В экономической теории, выявляющей основные, принципиальные взаимосвязи и взаимозависимости в экономике, различия между разными видами процентных ставок полагаются несущественными и под рыночной ставкой процента понимается средняя из всех различных ставок.

Соотношение между автономными планируемыми расходами и ставкой процента. Изменение ставки процента влияет на следующие компоненты автономных расходов:

• инвестиционные расходы. Занимая средства на покупку инвестиционных товаров, фирмы пытаются получить прибыль. Поэтому они инвестируют средства в оборудование и промышленные сооружения (приобретают реальный капитал) до тех пор, пока норма отдачи от дополнительной единицы капитала превышает стоимость заемных средств на покупку этой дополнительной единицы, т.е. ставку процента. Любое повышение ставки процента снижает эффективность инвестиционных проектов. Поэтому, если ставка процента настолько высока (кредитные средства дороги), что ожидаемая норма прибыли ниже этой ставки, фирма откажется от реализации такого инвестиционного проекта и величина инвестиционных расходов сократится. Следовательно, зависимость между величиной инвестиционных расходов и ставкой процента обратная. Чем выше ставка процента, тем меньше у фирм желание инвестировать. Функция инвестиций может быть записана: I = I (R) или, если зависимость линейная:

I = I – dR, где I – автономные инвестиции, R — ставка процента, d -коэффициент, отражающий чувствительность инвестиционных расходов к ставке процента и показывающий, насколько изменится величина инвестиционных расходов при изменении ставки процента на один процентный пункт. Коэффициент d>0, а поскольку перед ним в формуле стоит знак «минус», кривая имеет отрицательный наклон.

Кривая совокупного инвестиционного спроса (рис. 1.(а)) отражает эту обратную зависимость вели-чины спроса на инвестиции от ставки процента.

Сдвиг кривой совокупных инвестиционных расходов происходит при изменении величины автономных инвестиций (I): их увеличение смещает кривую вправо, а их сокращение — влево. Эти изменения, как правило, представители кейнсианского направления связывают с настроением инвесторов, пессимистической или оптимистической оценкой ожидаемой прибыльности инвестиционных расходов Последствия увеличения уровня автономных инвестиций показано на рис. 1.(б) сдвигом кривой I вправо до I’.

Наклон кривой совокупных инвестиционных расходов обусловлен величиной коэффициента d; чем он выше, т.е. чем более чувствительны инвестиции к изменению ставки процента, тем кривая I более пологая: даже незначительные изменения ставки процента ведут к существенным изменениям величины инвестиционного спроса.

• потребительские расходы. Аналогично инвесторам, домохозяйства также используют заемные средства, особенно при покупке потребительских товаров длительного пользования. Потребители сравнивают процентные выплаты по долгу (потребительскому кредиту) с желанием приобрести товар (например, автомобиль или посудомоечную машину) как можно раньше. Высокие процентные ставки заставляют некоторых потребителей отложить покупку до лучших времен и автономные потребительские расходы сокращаются. Таким образом, зависимость между совокупными автономными потребительскими расходами и ставкой процента обратная и все рассуждения и выводы аналогичны тем, которые сделаны относительно инвестиционных расходов (не случайно, некоторые экономисты предлагают рассматривать расходы на потребительские товары длительного пользования как инвестиционные расходы домохозяйств). Таким образом, потребительские расходы зависят не только от уровня располагаемого дохода, но и от ставки процента, и потребительская функция может быть представлена формулой: С = С (Y, Т, t, R) или при линейной зависимости: С = С + mpс (Y – Т- tY) — аR, где С — автономные потребительские расходы, Y — доход, Т- автономные чистые налоги (налоги Tx минус трансферты Tr), mpс – предельная склонность к потреблению (0 0), отражающая изменение потребительских расходов при изменении ставки процента на один процентный пункт (a=ΔC/ΔR),

• расходы на чистый экспорт. Изменение ставки процента оказывает влияние и на величину чистого экспорта. Рост процентной ставки в стране повышает доходность вкладываемого капитала и обусловливает приток капитала из-за рубежа. В результате спрос на национальную валюту данной страны на валютных рынках растет, и национальная валюта дорожает. Это ведет к тому, что товары данной страны становятся относительно более дорогими, а импортные товары относительно более дешевыми. Спрос на национальные товары со стороны иностранцев падает, сокращая экспорт, а спрос на иностранные товары растет, увеличивая импорт. Чистый экспорт сокращается, уменьшая совокупные расходы. Следовательно, и между чистым экспортом и ставкой процента существует обратная зависимость.

Поэтому формула экспорта может быть представлена как: Хn = Xn (Y, e) или при линейной зависимости: Хn = Ех — (Im + mpm Y) – eR = Хn – mpm Y — eR,

где Ех – автономный экспорт; Im – автономный импорт; Хn – автономный чистый экспорт; mpm — предельная склонность к импорту (0 0), показывающая изменение величины чистого экспорта, если ставка процента меняется на один процентный пункт (ΔXn/ΔR).

Построение кривой IS. Поскольку величина планируемых автономных расходов зависит от ставки процента,а общий уровень реального выпуска и реального дохода зависит от величины автономных планируемых расходов, то если объединить вместе эти зависимости, можно придти к выводу, что реальный доход должен зависеть от ставки процента. Изобразив это соотношение графически, мы получим кривую IS. Выведем график кривой IS двумя способами:

На рис. 2.(а) кривая IS выведена из Кейнсианского креста и функции инвестиций. При ставке процента R₁ величина инвестиционных расходов равна I₁, что соответствует величине планируемых расходов Ер₁, при которой величина совокупного дохода (выпуска) равна Y₁. Когда ставка процента снижается до R₂, величина инвестиционных расходов возрастает до I₂, поэтому на графике Кейнсианского креста кривая планируемых расходов сдвигается вверх до Ер₂, чему соответствует величина совокупного дохода (выпуска) Y₂. Таким образом, более высокой ставке процента R₁ соответствует более низкий уровень совокупного выпуска Y₁, а более низкой ставке процента R₂ соответствует более высокий уровень выпуска Y₂. Причем и в том, и в другом случае товарный рынок находится в равновесии, т.е. расходы равны доходу (Ер₁=Y₁ и Ер₂=Y₂). Это и отражает кривая IS, каждая точка которой показывает парные сочетания ставки процента и уровня дохода, при которых товарный рынок находится в равновесии.

На рис. 2.(б) кривая IS выводится из принципа равенства инъекций (инвестиций) и изъятий (сбережений) (что является условием равновесия товарного рынка), который следует из основного макроэкономического тождества:

С + I + G + Ex = C + S + T + Im

Вычтем из обеих частей равенства потребительские расходы С, получим:

I + G + Ex = S + T + Im

В правой части равенства – инъекции (injections) — расходы, которые увеличивают поток доходов, а в левой части – изъятия (leakages) — переменные, которые сокращают доходы. В равновесной экономике расходы равны доходам, а инъекции равны изъятиям. Инъекции отрицательно зависят от ставки процента, а изъятия положительно зпависят от уровня дохода. С учетом этих зависимостей можно записать:

I (R) + G + Ex (R) = S (Y) + T (Y) + Im (Y)

На рис. 2.(б) изображены 4 графика. На I графике показано условие равновесия товарного рынка — равенство инъекций (представленных инвестициями) и изъятий (представленных сбережениями), что графически отражает биссектриса угла (линия под углом 45 o ). На II графике представлен график прямой зависимости изъятий от дохода. На III графике показана обратная зависимость инъекций от ставки процента. В результате на IV графике получаем кривую IS. При ставке процента R₁ величина инъекций составляет I₁, что соответствует величине изъятий S₁, а такая их величина будет при уровне дохода Y₁. Аналогично, при ставке процента R₂ величина инъекций будет равна I₂, при которой величина изъятий составит S₂, что соответствует уровню дохода Y₂. Соединив полученные на IV графике точки прямой линией, получим кривую IS.

Кривая IS показывает все возможные комбинации уровней ставки процента (R) и реального дохода (Y), при которых товарный рынок находится в равновесии, т.е. спрос на товары и услуги равен их предложению, что происходит лишь в случае, когда доход равен планируемым расходам, а инъекции равны изъятиям.

Точки вне кривой IS. В любой точке, находящейся вне кривой IS, экономика находится в неравновесии. Например, в т.А (рис. 2.(б)), которая находится выше кривой IS, величина дохода равна Y₂, что соответствует величине изъятий S₂, а ставка процента составляет R₁, при которой величина инъекций равна I₁. В этом случае изъятия превышают инъекции (S₂ > I1), что означает, что на товарном рынке доход (выпуск) превышает расходы, т.е. предложение товаров превышает спрос на товары. Следовательно, во всех точках, находящихся выше кривой IS, существует избыточное предложение товаров (excess supply of goods – ESG).

В т. В, находящейся ниже кривой IS, величина дохода равна Y₁, что соответствует величине изъятий S₁, а ставка процента равна R₂, что соответствует величине инъекций I₂. Поскольку I₂ > S₁, это значит, что инъекции больше изъятий, т.е. расходы превышают доход (выпуск), следовательно, спрос больше предложения. Таким образом, во всех точках, находящихся ниже кривой IS, наблюдается избыточный спрос на товары (excess demand for goods – EDG).

Наклон кривой IS. Кривая IS имеет отрицательный наклон, поскольку более высокий уровень ставки процента вызывает уменьшение инвестиционных, потребительских расходов и расходов на чистый экспорт, и, следовательно, совокупного спроса (совокупных расходов), что ведет к более низкому уровню равновесного дохода. И наоборот, более низкая ставка процента увеличивает автономные планируемые расходы, а более высокий уровень автономных расходов увеличивает доход в k_A раз, где k_A — это полный мультипликатор (или супермультипликатор) расходов.

Наиболее полное представление о взаимосвязях между уровнем дохода (Y) ставкой процента (R) и особенностях кривой IS дает ее алгебраический анализ.

Алгебраический анализ кривой IS. Вспомним, что равновесный уровень дохода устанавливается тогда, когда объем выпуска (Y) равен совокупным планируемым расходам (Е = С + I + G + Xn). Мы предполагаем, что функция потребления, функция инвестиций и функция чистого экспорта линейны и зависят от ставки процента:

С = С + mpс (Y – Т- tY) — аR

Хn = Ех — (Im + mpmY) — eR= Хn – mpmY — eR

Равновесный доход равен:

Y = (C – mpcT + I + G + Xn – bR)/(1 – mpc (1 — t) + mpm)

где b = (a+d+e) и является коэффициентом чувствительности автономных расходов к ставке процента, показывая, насколько изменятся автономные расходы при изменении процентной ставки на один процентный пункт.

Поскольку С – mpcT + I + G + Xn = A (сумма автономных расходов) и [1/(1- mpс(1 — t) + mpm)] = k_A (полный мультипликатор расходов), то уравнение кривой IS может быть представлено: Y = k_A (A — bR) или для ставки процента как: R = A/b — (1/k_Ab)Y

Так как коэффициент b > 0 и имеет перед собой знак «минус», то кривая IS имеет отрицательный наклон. Сдвиги кривой IS. Сдвиги кривой IS обусловлены изменениями любого из компонентов автономных расходов (C, I, G или Xn) и автономных чистых налогах (Tx или Tr). Все, что увеличивает автономные расходы (оптимизм предпринимателей и потребителей, усиливающий их желание увеличивать расходы при любой ставке процента, что ведет к росту потребительских и инвестиционных расходов; рост государственных расходов; снижение автономных (аккордных) налогов; увеличение трансфертных выплат; рост чистого экспорта), сдвигает кривую IS вправо. Если же автономные расходы по какой-то причине снижаются, кривая IS сдвигается влево. Сдвиг кривой и в том, и в другом случае параллельный и происходит на расстояние, равное k_AΔА, (так как ΔY=k_AΔА), т.е. расстояние сдвига при неизменной ставке процента определяется величиной изменения автономных расходов и величиной мультипликатора расходов. Чем на большую величину изменяются автономные расходы и/или чем больше величина мультипликатора, тем на большее расстояние сдвигается кривая.

Наклон кривой IS. Наклон кривой IS равен 1/(k_Ab) или МLR/b, где MLR — предельная норма изъятий (вспомним, что MLR = 1 – mpc (1 — t) + mpm = mps (1 — t) + t + mpm, т.е. предельная норма изъятий — это величина, обратная мультипликатору расходов, MLR = 1/k_A). Таким образом, наклон кривой IS определяется: 1) чувствительностью автономных расходов к ставке процента (b), 2) величиной мультипликатора (kA), которая зависит от предельной склонности к потреблению (mpс), налоговой ставки (t) и предельной склонности к импорту (mpm).

Наклон кривой IS уменьшается (она поворачивается по часовой стрелке и становится более пологой). Кривая IS будет более пологой:

• чувствительность автономных расходов к ставке процента (b) велика, что означает, что даже незначительное изменение ставки процента ведет к существенному изменению автономных расходов и, следовательно, дохода;

• мультипликатор расходов (k_A) велик, а предельная норма изъятий (MLR) мала, что возможно, если: а) предельная склонность к потреблению велика; б) предельная налоговая ставка мала; в) предельная склонность к импорту мала. Если мультипликатор велик, то это означает, что даже несущественное изменение автономных расходов приведет к большому мультипликативному изменению дохода. (Заметим, что величина мультипликатора обусловливает и наклон, и величину сдвига кривой IS).

Таким образом, рост b и mpc и снижение t и mpm уменьшают наклон IS.

Наклон кривой IS увеличивается (она поворачивается против часовой стрелки и становится более крутой), когда величина b и/или k_A уменьшается.

Кривая IS однако не определяет ни конкретного значения уровня дохода Y, ни единственного значения равновесной ставки процента R, она лишь отражает все возможные комбинации Y и R, при которых рынок товаров и услуг находится в равновесии. Поэтому, чтобы определить их значения, необходимо еще одно уравнение с этими же переменными. Для этого следует обратиться к денежному рынку.

Кривая LМ

Равновесие на денежном рынке определяет кривая LM (liquidity preference — money supply), которая показывает все возможные соотношения Y и R, при которых спрос на деньги равен предложению денег. Под деньгами при этом, как правило, понимают денежный агрегат М1, включающий наличные деньги и средства на текущих счетах (demand deposits — чековых счетах или счетах до востребования), которые в любой момент можно легко превратить в наличность.

В основе построения кривой LM лежит кейнсианская теория предпочтения ликвидности, объясняющая, как соотношение спроса и предложения реальных запасов денежных средств (real money balances) определяют ставку процента. Реальные запасы денежных средств представляют собой номинальные запасы, скорректированные на изменение уровня цен и равны М/Р.

В соответствии с теорией предпочтения ликвидности, предложение реальных денежных средств (М/Р) S фиксировано и определяется центральным банком, контролирующим величину наличности С и резервов R, т.е. денежную базу (Н — high powered money; Н = С + R). Поскольку предложение денег является экзогенной величиной и не зависит от ставки процента, графически оно может быть представлено вертикальной кривой.

Спрос на реальные денежные запасы (М/Р) D включает в себя все виды спроса на деньги, а именно: 1) трансакционный спрос на деньги, представляющий собой спрос на деньги для покупки товаров и услуг (спрос на деньги для совершения сделок, т.е. для трансакций), вытекающий из функции денег как средства обращения и их свойства абсолютной ликвидности и положительно зависящий от уровня дохода (М/Р) D _Т = (М/Р) D (Y); 2) спрос на деньги из мотива предосторожности, также положительно зависящий от уровня дохода; 3) спекулятивный спрос на деньги, проистекающий из функции денег как запаса ценности, т.е. как финансового актива и отрицательно зависящий от ставки процента, которая в кейнсианской модели представляет собой альтернативные издержки хранения наличных денег, показывая потерю человеком дохода в случае, если все свои финансовые активы он хранит в виде наличных денег, отказываясь от покупки доходных (приносящих процентный доход) ценных бумаг (облигаций): (М/Р) D _A = (М/Р) D (R). Чем выше ставка процента, тем меньше денег целесообразно иметь в виде наличности. Чем ставка процента ниже, тем более притягательным становится свойство ликвидности, и люди начинают продавать облигации, увеличивая сумму наличных денег. (Не случайно теория денег Кейнса носит название «теории предпочтения ликвидности»). Таким образом, человек предпочитает иметь так называемый «портфель» финансовых средств, в который входят и наличные деньги, и ценные бумаги. Структура портфеля, т.е. соотношение в нем денежных и неденежных финансовых активов, меняется в зависимости от динамики ставки процента. Она будет оптимальной в том случае, если дает максимальный доход при минимальном риске.

В результате, если функции спроса на деньги линейны, общий спрос на деньги можно записать как функцию:

где (М/Р) D _Т – реальный трансакционный спрос на деньги, (М/Р) D _A – реальный спекулятивный спрос на деньги, Y- реальный доход, k — чувствительность спроса на деньги по доходу или коэффициент ликвидности, т.е. положительный коэффициент, показывающий, насколько изменяется реальный спрос на деньги при изменении уровня дохода на единицу; R — ставка процента, h — чувствительность спроса на деньги к ставке процента или положительный коэффициент, показывающий, как изменится реальный спрос на деньги при изменении ставки процента на один процентный пункт; знак «минус» перед h означает обратную зависимость (увеличение ставки процента сокращает спрос на деньги и наоборот).

В результате кривая общего спроса на деньги имеет отрицательный наклон, обусловленный его обратной зависимостью от ставки процента.

Поскольку предложение денег (М) определяет центральный банк, то это величина экзогенная и фиксированная и графически представляет собой вертикальную кривую.

Равновесие на денежном рынке устанавливается в точке пересечения кривой спроса на деньги с кривой предложения денег. Экономический механизм установления этого равновесия также объясняет кейнсианская теория предпочтения ликвидности, которая основана на положении об отрицательной зависимости между ставкой процента и ценой облигации. Движение ставки процента к равновесию происходит потому, что люди начинают менять структуру портфеля своих активов. (При равновесной ставке процента соотношение денежных и неденежных активов в портфеле является оптимальным). К изменению ставки процента ведет как изменение спроса на деньги, так и изменение предложения денег. Если спрос на деньги увеличивается, а предложение остается без изменения, ставка процента повышается, так как люди будут продавать облигации. На рынке облигаций предложение начинает превышать спрос, и цена облигаций падает. А поскольку цена облигации находится в обратной зависимости со ставкой процента, то ставка растет.

Ставка процента увеличивается и в том случае, когда центральный банк снижает предложение денег. Уменьшение денежной массы заставляет людей продавать облигации, что будет иметь результат, аналогичный представленному выше. И наоборот. Если спрос на деньги уменьшается, либо Центральный банк увеличивает предложение денег, ставка процента падает.

Однако не только величина процентной ставки R оказывает влияние на величину спроса на реальные денежные запасы, воздействуя на равновесие денежного рынка. Уровень дохода Y также влияет на спрос на деньги. Когда доход высок, расходы велики, люди вступают в большее количество сделок, покупая большее количество товаров и услуг и увеличивая трансакционный спрос на деньги.

Используя эти зависимости, можно построить кривую равновесия денежного рынка — кривую LM, показывающую связь между ставкой процента (R) и уровнем дохода (Y).

Построение кривой LM. Кривая LM показывает все комбинации уровня дохода Y и ставки процента R, при которых денежный рынок находится в равновесии, т.е. при которых реальный спрос на деньги равен реальному предложению денег: (М/Р) D =(M/P) S . Построим кривую LM двумя способами:

На рис. 3.(a) кривая LM строится на основе графика равновесия денежного рынка (выводимого из кейнсианской теории предпочтения ликвидности). Рост уровня дохода (от Y₁ до Y₂) увеличивает спрос на деньги, смещая кривую М D вправо, что увеличивает ставку процента от R₁ до R₂. Это позволяет построить кривую LM, показывающую, что для обеспечения равновесия денежного рынка более высокому уровню дохода будет соответствовать более высокая ставка процента. Поэтому наклон кривой LM положительный.

На рис.14.3.(б) кривая LM (IV график) выводится из принципа равенства общего спроса на деньги (включающего: 1) трансакционный спрос на деньги, зависящий от дохода и представленный кривой (M/Р)DT на II графике, и 2) спекулятивный спрос на деньги, зависящий от ставки процента и изображенный кривой (M/Р) D _A на III графике) предложению денег (кривая (M/Р) S , представленная на I графике в III квадранте, где показано бюджетное ограничение, налагаемое фиксированным количеством денег в экономике). При уровне дохода Y₁ трансакционный спрос на деньги равен [(M/Р) D _T]₁ , то при существующей в экономике величине предложения денег спекулятивный спрос на деньги составит [(M/P) D _A]₁, что соответствует ставке процента R₁. Если уровень дохода возрастет до Y₂, трансакционный спрос на деньги составит [(M/P) D _T]₂, при котором спекулятивный спрос на деньги равен [(M/P) D _A]₂, что соответствует ставке процента R₂. Таким образом, более высокому уровню дохода соответствует более высокая ставка процента.

Точки вне кривой LM. Все точки, находящиеся вне кривой LM, соответствуют неравновесию денежного рынка. Рассмотрим точку А (рис. 3.(б)), которая находится выше кривой LM. В этой точке уровень дохода равен Y1, что соответствует величине трансакционного спроса на деньги [(M/P) D _T]₁, а ставка процента составляет R2, что соответствует величине спекулятивного спроса на деньги (M D _A)₂. Сумма этих величин спросов на деньги соответствует величине предложения денег, характеризуемое точкой A’, лежащей на кривой, где предложение денег меньше, чем имеющееся в экономике (кривая (M/P)sup>S ). Таким образом, во всех точках, лежащих выше кривой LM, предложение денег превышает общий спрос на деньги, что означают избыточное предложение денег (excess supply of money – ESM). В точке В, которая находится ниже кривой LM трансакционный спрос на деньги составит [(M/P) D _T]₂, поскольку уровень дохода равен Y₂, а спекулятивный спрос на деньги равен [(M/P) D _A]₁, так как ставка процента равна R₁. Сумма спросов на деньги соответствует величине предложения денег в точке B’, где оно меньше, чем имеется в экономике. Таким образом, в этом случае спрос на деньги оказывается выше предложения денег. Следовательно, во всех точках, находящихся ниже кривой LM, имеет место избыточный спрос на деньги (excess demand for money – ESM). Чтобы в этих точках установилось равновесие, необходимо, чтобы либо изменился уровень дохода, либо величина ставки процента, либо и то, и другое. Если снижается ставка процента, то спрос на деньги увеличивается; если снижается уровень дохода, спрос на деньги падает.

Алгебраический анализ кривой LM. Полагая, что функция спроса на деньги линейна, можно получить алгебраическое выражение для кривой LM:

где (М/Р) S – предложение денег, kY – трансакционный спрос на деньги, (- hR) – спекулятивный спрос на деньги. Из этого уравнения получаем значение уровня равновесного дохода:

Y = (1/k)(M/P) S + (h/k)R (1)

и значение равновесной ставки процента:

R = (k/h)Y — (1/h)(M/P) S (2)

Уравнение равновесного дохода дает величину дохода, которая обеспечивает равновесие денежного рынка при любом значении ставки процента и величине реального предложения денег. Аналогично, уравнение равновесной ставки процента показывает величину ставки, которая дает равновесие на рынке денег при любом значении дохода и величине реального предложения денег. Вдоль кривой LM величина реального предложения денег фиксирована.

Поскольку коэффициент при Y в уравнении (2) положительный (k/h > 0, так как k > 0 и h > 0), кривая LM имеет положительный наклон и отражает прямую зависимость между уровнем дохода и ставкой процента. Более высокий доход предопределяет более высокий спрос на деньги, что ведет к более высокой ставке процента.

Сдвиги кривой LM. Сдвиги кривой LM обусловлены изменением номинального предложения денег (М S ). Поскольку уровень цен фиксирован (Р=соnst), то изменение центральным банком количества денег в обращении, меняет реальное предложение денег (М/Р) S . Так как коэффициент при (М/Р) S в уравнении (1) положительный, то рост предложения денег ведет к сдвигу кривой вправо на расстояние ΔМ(1/k), в то время как его сокращение сдвигает кривую на такое же расстояние влево.

Наклон кривой LM. Наклон кривой LM равен (k/h) — коэффициенту, стоящему перед Y в уравнении (2), и зависит от двух параметров: 1) чувствительности спроса на деньги к уровню дохода (k) и 2) чувствительности спроса на деньги к ставке процента (h).

Уменьшение h увеличивает наклон кривой LM (она становится более крутой) и при h = 0 кривая становится вертикальной. При росте h кривая LM становится более пологой. При уменьшении k кривая LM будет более пологой, а при его увеличении – более крутой.

Таким образом, кривая LM будет более пологая, если:

•чувствительность спроса на деньги к изменению ставки процента (h) велика (спрос на деньги чувствителен к изменению ставки процента). Это означает, что даже незначительное изменение ставки процента ведет к существенному изменению спроса на деньги;

•чувствительность спроса на деньги к изменению дохода (k) невелика (спрос на деньги нечувствителен к изменению дохода). Существенное изменение дохода вызывает незначительное изменение спроса на деньги.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Кривая IS. Ее выведение и значение.

Свое наименование линия IS (от англ. investment – savings) получила на основании того, что в равновесном состоянии на рынке благ инвестиции (I) равны сбережениям (S). Модель IS характеризует «реальный сектор» экономики— рынок благ. Равновесие на нем будет достигнуто при I = S, т.к. С = Y — S всегда.

Основные уравнения модели IS:

1) Y = C + I + G + NX — основное макроэкономическое тождество;

2) С = C_a + Ь (У — Т) — функция потребления, где T = T_a + tY;

3) I = I_a — dr — функция инвестиций;

4) NX = NX_a — m 1 Y — nr — функция чистого экспорта;

Эндогенные переменные модели: Y, С, I, NX, r.

Экзогенные переменные модели: G, t.

Остальные параметры и коэффициенты являются эмпирическими. Они положительны и относительно стабильны.

Поскольку Р = const, постольку номинальные и реальные значения всех переменных совпадают. В долгосрочном периоде, когда экономика находится в состоянии полной занятости ресурсов и уровень цен подвижен, все переменные модели представляются реальными (корректируются на Р).

Модель IS представляет собой все комбинации Y и r, которые одновременно удовлетворяют тождеству дохода, функциям потребления, инвестиций и чистого экспорта. Во всех точках кривой IS соблюдается равенство инвестиций и сбережений.

Уравнение кривой IS может быть получено путем подстановки уравнений 2, 3 и 4 в 1, т.е. в основное макроэкономическое тождество и его решения относительно r и Y.

Уравнение кривой IS относительно r имеет вид:

C_a + I_a + NX_a 1 – b(1 – t) + m 1 1 b

d + n d + n d + n d + n

Относительно Y уравнение имеет вид:

1 – b(1 – t) + m 1 1 – b(1 – t) + m 1 1 – b(1 – t) + m 1

d + n

— ——————— r

1 – b(1 – t) + m 1

Простейший графический вывод кривой IS связан с использованием функций сбережений и инвестиций (см. рис. 6.1).

S 3) S 2)

S₂ S₂

S₁ S₁

45 0

Y₁ Y₂ Y I₁ I₂ I

r 4) r 1)

r₁ r₁

Квадрант 1 представляет простую функцию инвестиций: движение от r₁ к r₂, что вызывает движение отI₁к I₂. Методом проекции отображаем изменение сбережений в квадранте 2, исходя из I = S. В квадранте 3 представлена известная нам функция сбережений, через которую можно проиллюстрировать изменение дохода (Y). В последнем 4 квадранте мы имеем возможность соединить в одной системе координат Y (из квадранта 3)иr (из квадранта 1). Через точки, полученные в результате пересечения проекций, проводим кривую IS. Аналогичные результаты могут быть получены с использованием модели креста Кейнса, но мы остановимся на самом простом варианте.

Кривая IS – это множество точек, каждая из которых показывает такое сочетание значений национального дохода и ставки процента при котором на рынке благ устанавливается равновесие.

Эта линия показывает, на сколько нужно изменить ставку процента (или уровень национального дохода) при изменении уровня наш национального дохода (или ставки процента) для сохранения равновесия на рынке благ.

Угол наклона кривой IS зависит от значений различных параметров и определяется коэффициентом

1 – b(1 – t) + m 1

d + n

Она становится более пологой, если:

1) чувствительность инвестиций (d) и чистого экспорта (n) к динамике ставки процента, предельная склонность к потреблению (b) повышаются;

2) предельная ставка налогообложения (t) и предельная склонность к импортированию (m’) понижаются.

Кривая LM. ее выведение и значение.

Модель LM (от англ. lquidity preference (предпочтение ликвидности) – money supply (денежное предложение)) определяет состояние равновесия на рынке денег. Она отражает равновесное соотношение общего спроса на деньги (L) и предложения денег (М).

Исходное уравнение модели — функция спроса на деньги в виде

— = kY — hr

Экзогенным параметром модели выступает предложение денег M S , величина фиксированная в коротком периоде. Эмпирические коэффициенты k и hположительны и относительно стабильны.

Модель LM представляет собой все комбинации Y и r, которые соответствуют равновесию на денежном рынке. Во всех точках кривой LM соблюдается равенство денежного спроса и предложения

Алгебраически модель LM может быть построена путем решения исходного уравнения относительно r и Y.

K 1 M

r = — Y — — • —

H h P

M h

Y = — • — + — r

K P k

Простейший вариант графического построения модели (см. рис. 6.2) LM основан на применении модели равновесия на денежном рынке, отражающей изменение спроса на деньги как результат изменения национального дохода: Y₂ > Y₁ => L₂ > L₁

r M S 1) r 2)

r₂ r₂

В квадранте 1 представлена модель денежного рынка. Повышение Y₁ до Y₂ обусловило движение от L₁ до L₂, что в свою очередь вызвало повышение савки процента с r₁ до r₂. Во втором квадранте сочетаем в одной системе координат ставку процента и НД. Через полученные методом проекции точки проводим кривую LM.

Кривая LM в каждой точке отражает комбинации ставки процента и национального дохода, при которых общий спрос на деньги равен предложению денег, т.е. достигнуто равновесие на денежном рынке.

Угол наклона кривой LM характеризуется коэффициентом k/h. Она становится более пологой, если: —

1) чувствительность спроса на деньги к динамике рыночной

ставки процента (h) растет;

2) чувствительность спроса на деньги к динамике объема выпуска (k) снижается.