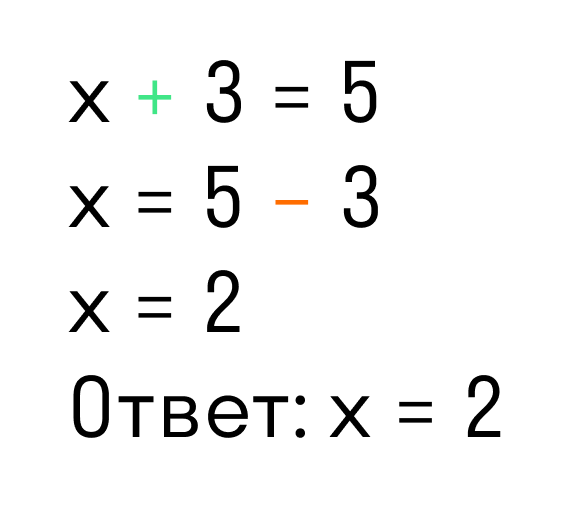Как выразить одну переменную через другую 7 класс в линейных уравнений

Уравнение с двумя переменными и его решение

Уравнение вида ax+by = c , где a,b,c — данные числа, называется линейным уравнением с двумя переменными x и y.

Например: 2x+5y = 6; -x+1,5y = 0; $frac$ x-8y = 7

Уравнение с двумя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x и y.

Например: $2x^2+y^2 = 3, x-5y^2 = 1, 7x^3+y = 7$

Решением уравнения с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y=6 решениями являются пары

x = -2, y = 2; x = -1,y = 1,6; x = -3,y = 2,4 и т.д.

Уравнение имеет бесконечное множество решений.

Свойства уравнения с двумя переменными

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

Уравнения с двумя переменными имеют такие же свойства, как и уравнения с одной переменной:

• если в уравнении перенести слагаемое из одной части в другую и изменить его знак, получится уравнение, равносильное данному;
• если обе части уравнения умножить или разделить на одно и то же, отличное от нуля число, то получится уравнение, равносильное данному.

Например: $2x+5y = 6 ⟺5y = -2x+6 iff y = -0,4x+1,2$

Примеры

Пример 1. Из данного линейного уравнения выразите y через x и x через y:

Алгоритм: рассмотрим 3x+4y=10

1) оставим слагаемое с выражаемой переменной с одной стороны, остальные слагаемые перенесем в другую сторону: 4y=-3x+10

2) разделим полученное уравнение слева и справа на коэффициент при выражаемой переменной: y=-0,75x+2,5 — искомое выражение y(x).

Аналогично для x(y): $3x+4y = 10 iff 3x = -4y+10 iff x = -1 frac y+3 frac$

Видео:Как выразить одну переменную через другую?Скачать

Урок алгебры в 7 классе «Способ Подстановки»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Конспект урока по алгебре в 7 классе на тему: «Метод подстановки»

Тип урока: урок открытия новых знаний

Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способом подстановки.

Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными.

Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, формирование умений применять приёмы: обобщения, сравнения, выделения главного.

Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.

Личностные: формирование желания приобретать новые знания, умения преодолевать трудности, осуществлять объективную самооценку успешности своей учебной деятельности.

Регулятивные: обнаружение и формулирование обучающимися учебной проблемы совместно с учителем; высказывание своего предположения, умение определить и сформулировать цель урока с помощью учителя, умение осуществлять контроль своих знаний и умений в процессе достижения результата в форме сравнений решений различными способами и его результата с заданным образцом с целью обнаружения ошибок, корректировать свои действия в случае расхождения.

Коммуникативные: умение вступать в диалог с учителем и одноклассниками, участвовать в коллективном обсуждении и взаимодействии.

Познавательные: умение работать с новой информацией, умение анализировать, синтезировать, сравнивать полученный результат.

Предметные: овладение алгоритмом решения системы двух уравнений с двумя переменными методом подстановки; умение применять на практике графический метод решения систем двух линейных уравнений и метод подстановки.

Технология проблемного обучения.

Оборудование: мультимедийное оборудование, проектор, экран, раздаточный материал.

Учебник Макарычев Ю.Н. Алгебра 7. Издательство «Мнемозина»

I . Организационный момент урока:

— Один из великих философов сказал: “ ГДЕ ЕСТЬ ЖЕЛАНИЕ, НАЙДЕТСЯ ПУТЬ!”. Я думаю, что сегодня на уроке мы с большим желанием будем решать системы, и не просто решать, а определяя свой рациональный путь.

— На прошлом уроке мы с вами познакомились с новой математической моделью. Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Ответим на несколько вопросов:

Теоретический фронтальный опрос (устно)

— Что такое решение системы? (Это пара значений, которая одновременно является решением всех уравнений системы)

— Что означает решить систему уравнений? (Значит найти все её решения или установить, что их нет) Слайд 4

— Является ли решением системы (Слайд 7)

пара чисел: а) х=3, у=1

1) Раскрыть скобки -2(х-3)= -2х+6

2) Выразить у через х

3) Выразить х через у

4) Решить уравнение

II . Актуализация опорных знаний

-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).

Алгоритм графического способа:

1. Построить графики каждого из уравнений системы.
2. Найти координаты точки пересечения построенных прямых (если они пересекаются)
3. Графический способ удобен, для определения количества корней ситемы уравнений.

Решить систему уравнений графическим способом (работаем в парах)

Задания делают на заранее приготовленных листах А4 с клетками, чтобы потом вывесить на доску, сравнить результаты и установить проблему урока.(слайд №14,15)

Создание проблемной ситуации и формулирование проблемы учениками.

— Решением первой системы являются дробные числа, которые трудно определить по графику. Решением второй системы являются большие числа, для определения которых не достаточно тетради.

— Можно ли использовать для решения данных систем уравнений графический способ?

— Я согласна, он не удачен в данной ситуации.

— Значит, чем мы займёмся сегодня на уроке?

— Таким образом, необходим какой- то другой способ решения систем уравнений, который нас не подведет в случае с дробными значениями координат точки.

III . Усвоение новых знаний и способов действий

Поиск решения проблемы

— В тетрадях запишите, пожалуйста, число.

— Тема урока: «Метод подстановки».

— Как вы думаете, какова цель нашего урока?

· узнать новый метод;

· получить алгоритм решения систем;

· научиться применять алгоритм.

— Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках.

Выразить переменную У через Х в следующих уравнениях: (К доске пойдет…)

(Вызвать к доске ученика, задание на доске, следить за устной речью ученика, ученик комментирует свое решение)

Ответ: у=2,5х у=8-1,5х.

Решаем из учебника у доски и в тетрадях № 12.7(а,б)

Задание 2. Слайд 5, 6 На слайде приведено решение системы двух линейных уравнений с двумя переменными методом подстановки.

Затем еще 2 примера и дети составляют алгоритм.

Описание решения проблемы.

— Составим алгоритм по ключевым словам:

— В учебнике найдите алгоритм решения и внимательно прочитайте его.

— Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.

— Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.

IV . Первичная проверка понимания нового материала

— Попробуем решить системы, которые вы решали в начале урока, но теперь методом подстановки:

— Кто может пойти к доске и выполнить это задание? (К доске…)

-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений — почему?

Сейчас мы с вами будем работать в парах: решаем №1069, а)

V . Творческое применение полученных знаний

— Существует, ребята, еще один способ решения систем уравнений, который мы с вами еще не рассматривали. Это метод — метод перебора или подбора. Например, дается система:

х + у = 7,

Можно легко подобрать значения х и у: х = 4, у = 3

-Попробуйте решить систему методом подбора:

х + у = 5

х 2 — у = 7, х = 3, у = 2

— Все эти способы решения систем уравнений знали люди давно. Точной даты неизвестно, но они имеются в книге Ньютона «Всеобщая арифметика», которая была издана в 1707 году.

VI . Подведение итогов

— В начале урока мы с вами ставили цели урока. Добились ли мы цели? Решили ли проблему? Чем будем заниматься на следующих уроках?

— Шёл мудрец, а навстречу ему три человека, везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил:

— Что ты делал целый день?
И тот с ухмылкою ответил, что целый день возил проклятые камни.
У второго спросил:

— А ты что делал целый день?

— Я добросовестно выполнял свою работу.

А третий улыбнулся, его лицо засветилось радостью и удовольствием, и он ответил:

— А я принимал участие в строительстве Храма

— Давайте и вы оцените свою работу на уроке. Перед вами три карточки: жёлтого, зеленого и красного цвета.

— Ребята! Кто работал так, как первый человек, поднимите жёлтые карточки.

— Кто работал добросовестно, как второй человек, поднимите зелёную карточку.

— А кто принимал участие в строительстве Храма знаний, поднимите карточку красного цвета.

Домашнее задание: знать алгоритм, № 1072 (б), № 1070(в,г),

Дополнительно в тетради.

Оценки сегодня получили… Спасибо за урок. До свидания.

Видео:Как в линейном уравнении с двумя переменными выразить одну переменную через другую и решить его.Скачать

Решение простых линейных уравнений

О чем эта статья:

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Как выразить х через у в линейном уравнении с двумя переменнымиСкачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

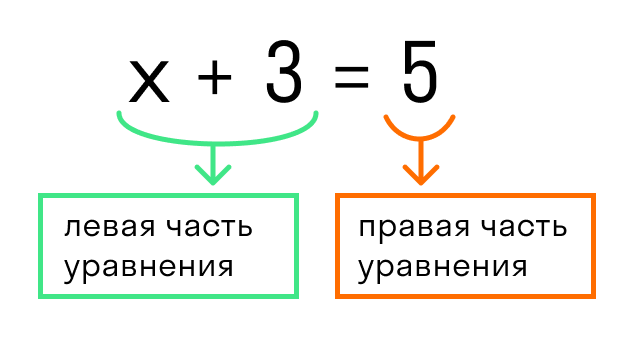
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

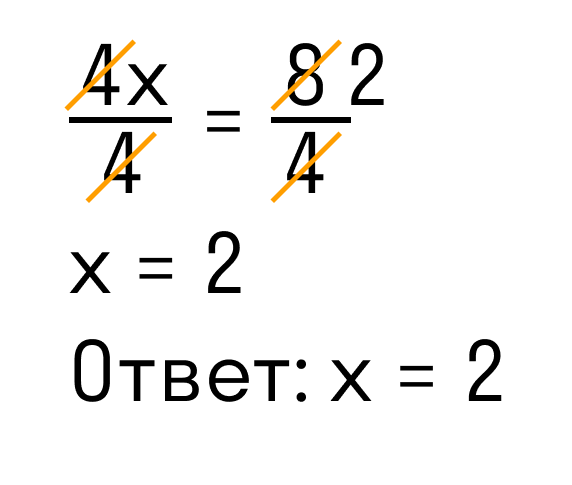
Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

🎦 Видео

Линейное уравнение и его разновидности. Алгебра 7 класс.Скачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Как выразить переменную из формулыСкачать

Выражение одной переменной через другую (алгебра 7 класс)Скачать

Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Выражение одной переменной через другую 7клСкачать

7 класс, 5 урок, Задачи на составление линейных уравнений с одной переменнойСкачать

Линейное уравнение с одной переменной. 6 класс.Скачать

Выразить переменнуюСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Видеоурок ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать