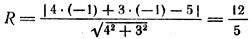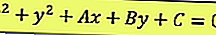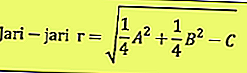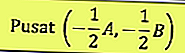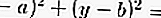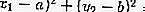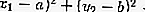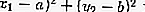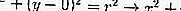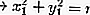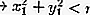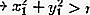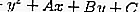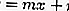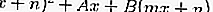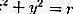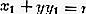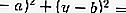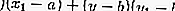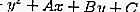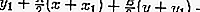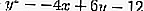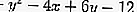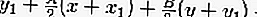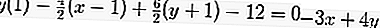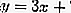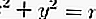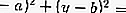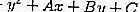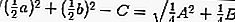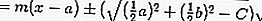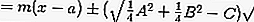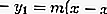Как выразить икс из уравнения окружности (2 видео)

Выразить переменную из уравнения

При решении систем линейных уравнений с многими переменными возникает частая необходимость выражения из уравнения той или иной переменной.

Как это делается? Возьмем для примера уравнение 2x+10y+3z=10. В нем наличествуют три переменных X, Y, Z. При помощи онлайнового калькулятора в зависимости от потребности выражения той или иной переменной уравнение 2x+10y+3z=10 преобразуется:
— через z в уравнение вида z = (-2x-10y+10)/(+3);
— через y в уравнение вида y = (-2x-3z+10)/(+10);
— через x в уравнение вида x= (-10y-3z+10)/(+2).

Полученное значение переменной X, Y или Z можно подставлять в следующее уравнение системы. В результате в нем будет на одну неизвестную переменную меньше. Выражение переменной из уравнений требуется при решении задач линейного программирования, направленных на выяснение значений показателей эффективности (целевой функции) в самых различных направлениях.

Решение систем линейных уравнений требуется для целей определения важных показателей сложных практических производственных и иных задач:
— загрузки оборудования,
— планирования производств,
— составления пищевого рациона откармливаемых животных,
— использования сырья и пр.

Содержание

Уравнение окружности
Уравнения окружности — формулы, общие формы и примеры задач
Круговые уравнения
Общее уравнение круга
В центре P (a, b) и радиуса r
At с центром O (0,0) и радиусом r
Пересечение линий и окружностей
Уравнения касательных к окружностям
1. Уравнение касательных через точку на окружности.
2. Касательные уравнения к градиенту
3. Уравнения касательных к точкам вне окружности.
Пример проблем
Пример проблемы 1
Пример проблемы 2
Пример проблемы 3
📽️ Видео

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

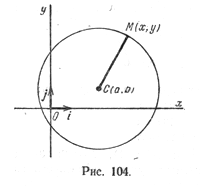
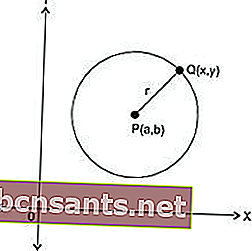
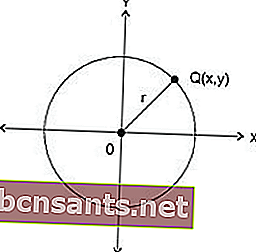
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

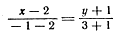
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

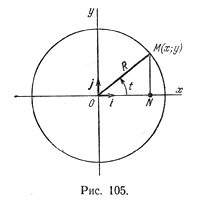
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнения окружности — формулы, общие формы и примеры задач

Уравнение окружности имеет общий вид x ^ 2 + y ^ 2 + Ax + By + C = 0, который можно использовать для определения радиуса и центра окружности.

Уравнение круга, которое вы узнаете ниже, имеет несколько форм. В разных случаях уравнение может быть разным. Поэтому хорошо его поймите, чтобы запомнить наизусть.

Круг — это набор точек, равноудаленных от точки. Координаты этих точек определяются путем составления уравнений. Это определяется на основе длины радиуса и координат центра круга.

Круговые уравнения

Существуют различные виды уравнений, а именно уравнения, составленные из центральной точки и радиуса, и уравнения, которые можно найти для центральной точки и радиуса.

Общее уравнение круга

Вот общее уравнение, как показано ниже:

Исходя из приведенного выше уравнения, можно определить центральную точку и радиус:

В центре P (a, b) и радиуса r

Из круга, если вы знаете центральную точку и радиус, вы получите формулу:

Если вы знаете центральную точку круга и радиус круга, где (a, b) — центр, а r — радиус круга.

Из полученного выше уравнения мы можем определить, лежат ли включая точки на окружности, внутри или снаружи. Чтобы определить местоположение точки, используя подстановку точки в переменных x и y, а затем сравнивая результаты с квадратом радиуса круга.

At с центром O (0,0) и радиусом r

Если центральная точка находится в точке O (0,0), то сделайте замену в предыдущей части, а именно:

Из приведенного выше уравнения можно определить положение точки на окружности.

Вне круга: Также прочтите: Art Is: Определение, Функция, Типы и Примеры [FULL]

Общий вид уравнения можно выразить в следующих формах.

(x — a) 2 + (y — b) 2 = r2, или

X2 + y2 — 2ax — 2by + a2 + b2 — r2 = 0, или

X2 + y2 + Px + Qy + S = 0, где P = -2a, Q = -2b и S = a2 + b2 — r2

Пересечение линий и окружностей

По кругу с уравнением x2 + y2 + Ax + By + C = 0 можно определить, не касается ли линия h с уравнением y = mx + n, не задевает или не пересекает ее, используя принцип дискриминанта.

Подставив уравнение 2 в уравнение 1, вы получите квадратное уравнение, а именно:

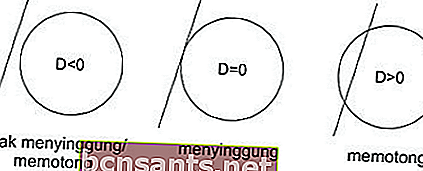
Из квадратного уравнения выше, сравнивая значения дискриминантов, можно увидеть, не задевает ли линия / не пересекает, не задевает или не пересекает круг.

Прямая h не пересекает / не задевает круг, поэтому D 0

Уравнения касательных к окружностям

1. Уравнение касательных через точку на окружности.

Касательные к окружности точно соответствуют точке, расположенной на окружности. Из точки пересечения касательной и окружности можно определить уравнение прямой касательной.

Уравнение касательной к окружности, проходящей через точку P (x ₁ , y ₁ ), может быть определено, а именно:

Форма

Уравнение касательной

Форма

Уравнение касательной

Форма

Уравнение касательной

Пример проблемы:

Уравнение касательной через точку (-1,1) на окружности

Знать уравнение круга

где A = -4, B = 6 и C = -12 и x ₁ = -1, y ₁ = 1

Итак, уравнение касательной

2. Касательные уравнения к градиенту

Если прямая с наклоном m касается окружности,

тогда уравнение касательной:

тогда уравнение касательной, заменив r на,

3. Уравнения касательных к точкам вне окружности.

Из точки вне круга можно провести две касательные к окружности.

Читайте также: Демократия: определение, история и типы [FULL]

Для нахождения касательного уравнения используется формула уравнения регулярной прямой, а именно:

Однако из этой формулы значение крутизны прямой неизвестно. Чтобы найти наклон прямой, подставьте уравнение для уравнения круга. Так как прямая является касательной, то из уравнения результат подстановки для значения D = 0, и значение m будет получено

Пример проблем

Пример проблемы 1

Круг имеет центр (2, 3) и имеет диаметр 8 см. Уравнение круга .

Обсуждение:

Поскольку d = 8 означает r = 8/2 = 4, поэтому уравнение для образующейся окружности имеет вид

(x — 2) ² + (y — 3) ² = 42

x² — 4x + 4 + y² -6y + 9 = 16

x² + y² — 4x — 6y — 3 = 0

Пример проблемы 2

Найдите общее уравнение для круга с центром в точке (5,1), нарушающего прямую 3 x — 4 y + 4 = 0!

Обсуждение:

Если известно, что центр окружности ( a , b ) = (5,1), а касательная к окружности равна 3 x — 4 y + 4 = 0, то радиус окружности определяется следующим образом.

Таким образом, общее уравнение для круга выглядит следующим образом.

Таким образом, общее уравнение для круга с центром в точке (5,1), нарушающего прямую 3 x — 4 y + 4 = 0, имеет вид

Пример проблемы 3

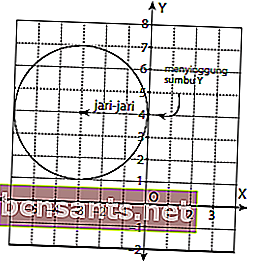
Найдите общее уравнение для круга с центром в точке (-3,4), нарушающего ось Y!

Обсуждение:

Прежде всего, давайте сначала нарисуем график круга, который с центром в (-3,4) и оскорбляет ось Y!

Основываясь на изображении выше, можно увидеть, что центр круга находится в координате (-3,4) с радиусом 3, так что:

Таким образом, общее уравнение с центром в точке (-3,4) и нарушением оси Y имеет вид

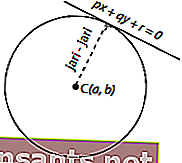
В некоторых случаях радиус окружности неизвестен, но известна касательная. Итак, как определить радиус круга? Посмотрите на следующую картинку.

Изображение выше показывает, что касательная к уравнению px + qy + r = 0 относится к окружности с центром в точке C ( a, b ). Радиус можно определить по следующему уравнению. а, б ). Радиус можно определить по следующему уравнению.