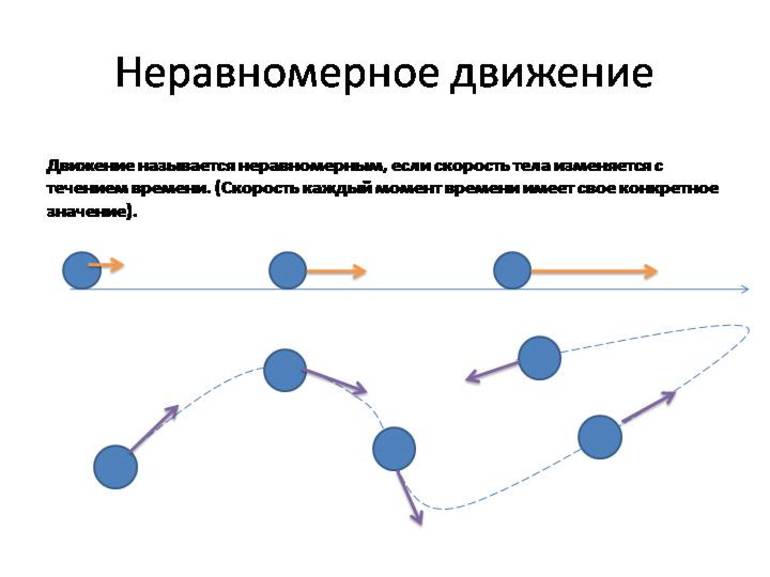
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.
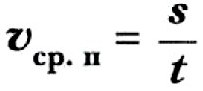
Средняя путевая скорость — скалярная неотрицательная величина.
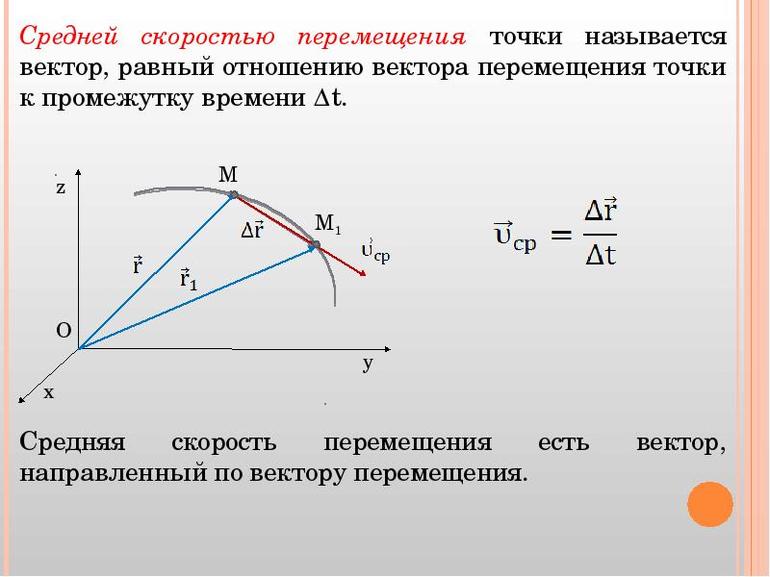
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения 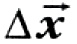
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
- Пример решения задач на среднюю скорость при неравномерном движении
- I. Механика
- Тестирование онлайн
- Виды неравномерного движения
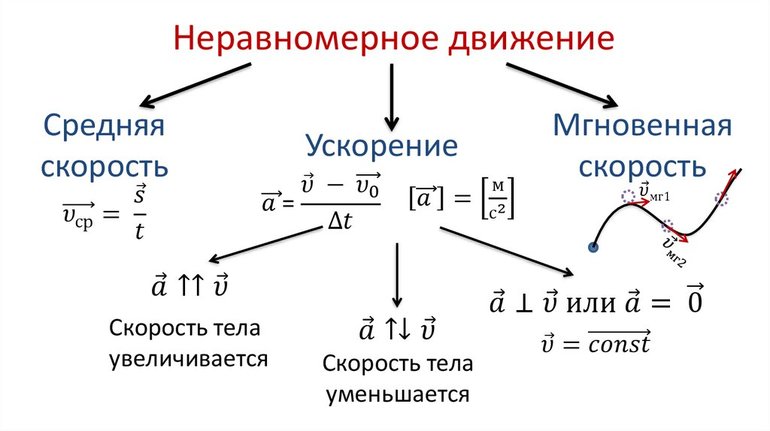
- Мгновенная скорость
- Средняя скорость
- Средняя скорость перемещения. Средняя путевая скорость
- Главное запомнить
- Формула для определения средней скорости*
- Определение мгновенной скорости графически*
- Упражнения
- Неравномерное движение — общая характеристика, формулы и примеры вычислений
- Основные понятия
- Суть и определение
- График движения
- Математическое описание
- Примеры решения задач
- 🌟 Видео
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»
Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
Видео:Решение графических задач на равномерное движениеСкачать

I. Механика
Видео:9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Тестирование онлайн
Видео:Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Виды неравномерного движения
Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.
Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения — равноускоренное движение.
Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.
Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Мгновенная скорость
Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!
Видео:Графическое представление равномерного движения.Скачать

Средняя скорость
Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость — это весь путь разделить на затраченное время. И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.

У средних величин рисуют сверху горизонтальную черту.
Видео:Равномерное прямолинейное движение - физика 9Скачать

Средняя скорость перемещения. Средняя путевая скорость
Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость — скаляр.
Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Главное запомнить
1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения
Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Формула для определения средней скорости*
Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.
Видео:Уравнение координат при равноускоренном движенииСкачать

Определение мгновенной скорости графически*
Мгновенную скорость можно определить с помощью графика движения. Мгновенная скорость тела в любой точке на графике определяется наклоном касательной к кривой в соответствующей точке. Мгновенная скорость — тангенс угла наклона касательной к графику функции.
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Упражнения
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.
Какую скорость переменного движения показывает спидометр автомобиля?
Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.
В каком случае мгновенная и средняя скорости равны между собой? Почему?
При равномерном движении. Потому что скорость не изменяется.
Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?
Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?
*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.
Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.
Видео:Прямолинейное равномерное и неравномерное движение. 7 класс.Скачать

Неравномерное движение — общая характеристика, формулы и примеры вычислений
Видео:1.1.4 Уравнение равнопеременного движенияСкачать

Основные понятия
Наука, изучающая механическое движение без учёта причин, его вызвавших, называется кинематикой. При перемещении в физике принимается, что любой объект состоит из множества одинаково движущихся материальных точек. Поэтому вместо того, чтобы рассматривать тело в целом, изучается только поведение одной точки.
Любое движение описывается рядом параметров. К основным из них относят:
- Траекторию — линию, по которой происходит перемещение в пространстве.
- Пройденное расстояние — путь, ограниченный начальными и конечными координатами.
- Координаты — изменение положения точки в пространстве относительно принятого начала.
- Скорость — быстрота изменения положения.
- Ускорение — нарастание скорости во времени.
Под перемещением понимают движение за некий промежуток времени, описываемый вектором: ∆r = r — r0. Направление вектора принимается от положения материальной точки в начальный момент, к изменению её расположения в установленный. Скорость же представляет вектор, определяющий направление перемещения и быстроту изменения движения относительно начальных координат, то есть какого-либо тела отсчёта.
Движение принято разделять на два вида: прямолинейное и криволинейное. В качестве примера для первого вида можно привести езду поезда на ровном участке железной дороги, бег спринтера на короткие дистанции, перемещение воды в прямой трубе. В реальности же чаще приходится сталкиваться с криволинейным перемещением, таким как падение тела, полёт футбольного мяча после удара.
Какой бы ни была траектория движения, под перемещением понимают минимальное расстояние, которое находится между отправной и конечной координатой. Фактически это — отрезок, соединяющий две точки. Но движение кроме траектории описывается и скоростью, то есть быстротой прохождения заданных участков.
Неравномерность перемещения обозначает изменение быстроты движения. Физическая величина, определяемая как отношение пройденного пути ко времени, затраченному на движение, называется средней скоростью. Этот параметр специально ввели для описания неравномерного движения в физике.
Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Суть и определение
Суть неравномерного движения изучают в седьмом классе средней школы на уроках физики. В школьном учебнике приводится определение, что неравномерным считается такое изменение материальной точки в пространстве, при котором меняется скорость. При этом отмечается, что она может изменяться и по направлению.
Исходя из этого, можно сделать заключение, что движение, сопровождающее изменением скорости или траектории, является неравномерным. Например, вращение шара по окружности, выстрел из лука. При этом перемещение может быть равноускоренным, то есть состоять из чередования различных неравномерных движений. Как пример можно привести переключение скоростей в передвигающемся автомобиле.
Средняя скорость — это относительный параметр. Определяется он отношением пройденного пути к затраченному для этого времени. Предполагать, что для его нахождения можно просто сложить известные мгновенные скорости и разделить результат на их количество, в корне неверно. Под мгновенной характеристикой понимается скорость, существующая в определённой точке на данный момент.
Например, спидометр, установленный в машине, регистрирует ежесекундно именно мгновенную скорость. Поэтому для нахождения среднего показателя используется следующая формула: V = s / t, где:
- V — искомая средняя скорость;
- s — пройденный путь;
- t — затраченное на прохождение время.
В качестве единицы измерения используется отношение метров на секунды в соответствии с Международной системой измерений (СИ). Следует отметить, что когда траектория пути не является прямолинейной, то пройденное материальной точкой расстояние будет больше, чем её перемещение. Для описания такого случая вводится понятие средней путевой скорости, являющейся скалярной величиной. При этом её значение будет отличаться от средней скорости перемещения.
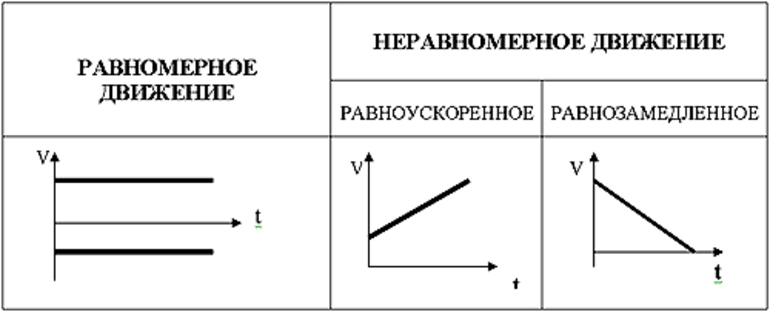
Случается так, что движение точки через один и тот же промежуток времени изменяется на одинаковую величину. В этом случае движение называют равнопеременным. Оно может быть как равнозамедленным, так и равноускоренным. Ускорение или замедление не зависит от изменения скорости за единицу времени. Но, зная поведение тела и его начальную скорость, можно вычислить, с какой скоростью оно будет двигаться в любой промежуток времени. Для этого используют выражение: v = v0 + a * Δt.
Видео:график равномерного движения #физика #графикСкачать

График движения
Существует простая геометрическая интерпретация траектории движения, по которой двигалась материальная точка. Когда тело перемещается с одной и той же скоростью, равняющейся v, то длительность пройденного отрезка будет определяться выражением: ∆t = t2 − t1, где t1 и t2 — начальный и конечный момент времени. Вполне логично предположить, что за указанный промежуток времени тело переместится на расстояние, равное: s = v * (t 2 — t 1) = v * ∆t.
В этом случае график пути в декартовой системе координат будет выглядеть как прямая. При этом пройденное расстояние, по сути, будет определяться площадью прямоугольника, построенного вниз от линии пути до оси времени. Скорость будет соответствовать вертикальной стороне фигуры, а изменение времени — горизонтальной.
Теперь можно рассмотреть, как будет выглядеть график неравномерного движения. Средняя скорость тела зависит от времени на конкретно взятом промежутке, ограниченном моментами t1 и t2. Пусть рассматриваемый отрезок будет разбит на промежутки, равные ∆t. Можно предположить, что в каждом таком отрезке скорость движения остаётся неизменной. Плавное её изменение можно заменить аппроксимацией ступенчатого вида. Иными словами, в каждом таком промежутке увеличение v (t) будет определяться выражением: v (t) ] = [ti, ti + ∆t].
Тогда ∆t будет совпадать с площадью прямоугольника, находящегося под ступенькой. Таким образом, путь будет определяться суммой всех площадей на графике. Когда ∆t направлена в сторону нуля, то сумма площадей этих прямоугольников будет располагаться под скоростью. То есть фактически — обозначать путь, пройденный телом с начальной точки до конечной.
Исходя из сказанного, можно утверждать, что расстояние, которая проходит точка при неравномерном движении, определяется площадью, находящейся под графиком скорости на установленном промежутке времени. Это определение является общим для любого типа перемещений.
Видео:Равномерное и неравномерное движениеСкачать

Математическое описание
Движение характеризуется различными параметрами, которые можно описать формулами и уравнениями. С точки зрения математики под термином понимается изометрия пространства в себя. При решении задач, связанных с неравномерным движением, используются следующие формулы:
- Вектор средней скорости. Определяется как отношение вектора изменения ко времени, за которое произошло перемещение: vср = Δs / Δt.
- Средняя путевая скорость. Для её вычисления используется отношение пройденного пути к отрезку времени, за которое преодолено это расстояние: v ¯ = l / Δt. Более общим выражением, описывающим этот параметр, будет отношение изменения координаты объекта к промежутку времени: v = Δx / Δt.
- Мгновенная скорость. Определяется формулой: v = lim Δs / Δt = lim Δr / Δt. При этом предел времени стремится к нулю. То есть характеристика численно равняется отношению изменения координаты ко времени, за которое оно произошло. Направление вектора параметра совпадает с траекторией движения. Следует отметить, что для прямолинейного движения скорость изменяется только по значению, а направление остаётся неизменным.
- Равнопеременное движение. Если вектор обозначить как Δv, то изменение скорости можно обозначить как Δv = v — v0. В случае когда Δt 1 = Δt 2 = … = Δtn, тогда Δv1 = Δv2 = … = Δvn. Отсюда Δv1 / Δt1 = Δv2 / Δt2 = … = Δv3 / Δt3 = cost. Другими словами, это характеристика движения, при которой a = (v — v 0) / t.
- Ускорение. Показывает зависимость изменения скорости от вектора к промежутку времени. Для неравномерного перемещения используется формула: a ср = Δv / Δt. Из неё следует, что мгновенное ускорение будет равняться: a = lim Δv / Δt = v’. Ускорение — это параметр, который определяется не только изменением модуля, но и вектором. Смысл заключается в том, что любое движение по окружности будет являться ускоренным из-за изменения направления в течение времени.
- Равнопеременное перемещение. График движения описывается уравнением: v = v0 + a * t.
Нужно отметить, что при равноускоренном движении расстояние изменяется в соответствии с квадратной зависимостью: s = v0 * t + at 2 / 2. В координатных прямых зависимость будет иметь вид: x = x0 + vo * t + a * t / 2. При этом график будет иметь вид параболы.
При расчётах довольно часто применяется закон сложения скоростей. Он позволяет определить параметр относительно зафиксированной системы отсчёта. Согласно этому способу: v2 = v1 + v. Понять справедливость утверждения можно, представив муху, ползущую по поверхности пластинки. Её скорость будет определяться относительно проигрывателя суммой движения и тем параметром, который имеет точка пластинки по отношению к площади, на которой находится в рассматриваемый момент тело.
Видео:Урок 15. Решение задач на графики движенияСкачать

Примеры решения задач
С помощью формулы неравномерного движения в физике решаются различные задания на расчёт ускорения и вычисление параметров перемещения в реальных условиях. Одной из типовых задач, предлагающихся для самостоятельного решения ученикам в школе, является следующая.
Пусть имеется автомобиль, который ехал по прямому шоссе со скоростью 90 км/час одну минуту. Затем он заехал на подъём, который преодолевал две минуты. Его движение замедлилось до 60 км/ч. Для съезда с него машина затратила 0,5 минут, спидометр при этом показывал 120 км/ч. Нужно вычислить среднюю скорость.
При использовании теоретических знаний и закона сложения формула, позволяющая найти ответ, будет выглядеть следующим образом: V = s / t = (s1 + s2 + s3) / (t1 + t2 + t3). По условию задачи, движение можно разделить на три части: прямое (шоссе), замедленное (подъём), ускоренное (спуск). Для каждого из участков нужно определить пройденное автомобилем расстояние. Так, s1 = v1 * t1 = 90 * 1/60 = 1,5 км; s2 = v2 * t2 = 60 * 2/60 = 2 км; s3 = v3 * t3 = 120 * 0,5/60 = 1 км. Подставив полученные значения, можно вычислить ответ: v = (1,5 + 2 + 1) / (3,5 / 60) = 77 км /ч. Число шестьдесят используется в формуле для перевода времени в систему СИ.
Вот ещё одна из типичных задач. Пусть велосипедист проехал за первый час десять километров. За последующие три часа он преодолел тридцать километров. Нужно найти среднюю скорость. Для решения задачи нужно обозначить всё расстояние, что проехал велосипедист, буквой r, а время, которое он затратил для его преодоления — t. Тогда V = r /t = (r1 + r2) / (t1 + t2) = (10 +30) / (1+3) = 40 / 4 = 10 км/ч.
Приведённые задачи относятся к заданиям среднего уровня. Из примеров более сложного типа можно привести следующий. Имеется шарик. Нужно так его направить на желобе, чтобы он скатывался с ускорением за три-четыре секунды. Замерить затраченное время секундомером.
Вначале следует определить длину жёлоба: l = v * t. Скорость будет определяться как (Vнач + Vкон) / 2, так как Vкон = Vнач + a * t. Учитывая, что Vнач = 0, то Vкон = 2 + Vср, а Vкон = a * t. Следовательно: a = (2 * Vср) / t. Из опыта было установлено — время равняется четырём секундам, а необходимое расстояние жёлоба — 120 см. Отсюда v = 120 / 4 = 30 см/с. Исходя из этого, Vк = 60 см/с, а ускорение будет: a = 2V /t = 60 /4 = 15 см/с2. Задача решена.
🌟 Видео
Равномерное и неравномерное движение | Физика 7 класс #10 | ИнфоурокСкачать

Прямолинейное движение. 10 класс.Скачать

Прямолинейное равномерное движениеСкачать

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать