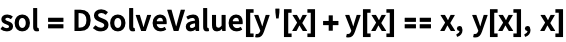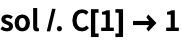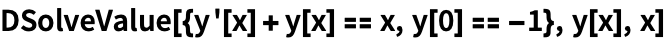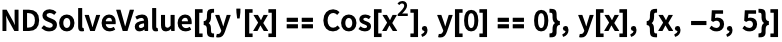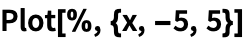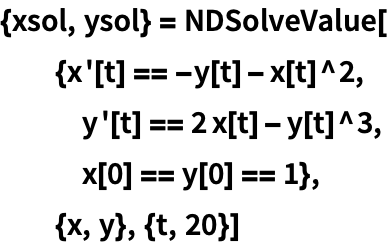1. Решение рациональных, дробно-рациональных уравнений любой степени, показательных, логарифмических, тригонометрических уравнений.
Пример 1 . Чтобы решить уравнение x 2 + 3 x — 4 = 0, нужно ввести solve x^2+3x-4=0
Пример 2. Чтобы решить уравнение log32x = 2 , нужно ввести solve log(3, 2x)=2
Пример 3. Чтобы решить уравнение 25 x-1 = 0.2 , нужно ввести solve 25^(x-1)=0.2
Пример 4. Чтобы решить уравнение sin x = 0.5 , нужно ввести solve sin(x)=0.5
2. Решение систем уравнений.
Пример . Чтобы решить систему уравнений
нужно ввести solve x+y=5 && x-y=1
Знаки && в данном случае обозначает логическое «И».
3. Решение рациональных неравенств любой степени.
Пример . Чтобы решить неравенство x 2 + 3 x — 4 solve x^2+3x-4
4. Решение систем рациональных неравенств.
Пример. Чтобы решить систему неравенств
нужно ввести solve x^2+3x-4 && 2х^2 — x + 8 > 0
Знаки && в данном случае обозначает логическое «И».
5. Раскрытие скобок + приведение подобных в выражении.
Пример . Чтобы раскрыть скобки в выражении (c+d) 2 (a-c) и привести подобные, нужно
ввести expand (c+d)^2*(a-c) .
6. Разложение выражения на множители.
Пример . Чтобы разложить на множители выражение x 2 + 3 x — 4, нужно ввести factor x^2 + 3x — 4 .
7. Вычисление суммы n первых членов последовательности (в том числе арифметической и геометрической прогрессий).
Пример . Чтобы вычислить сумму 20 первых членов последовательности, заданной формулой an = n 3 +n, нужно ввести sum n^3+n, n=1..20
Если нужно вычислить сумму первых 10 членов арифметической прогрессии, у которой первый член a 1 = 3, разность d = 5, то можно, как вариант, ввести a1=3, d=5, sum a1 + d(n-1), n=1..10
Если нужно вычислить сумму первых 7 членов геометрической прогрессии, у которой первый член b 1 = 3, разность q = 5, то можно, как вариант, ввести b1=3, q=5, sum b1*q^(n-1), n=1..7
8. Нахожд ение производной.
Пример . Чтобы найти производную функции f(x) = x 2 + 3 x — 4, нужно ввести derivative x^2 + 3x — 4
9. Нахожд ение неопределенного интеграла.
Пример . Чтобы найти первообразную функции f(x) = x 2 + 3 x — 4, нужно ввести integrate x^2 + 3x — 4
10. Вычисление определенного интеграла.
Пример . Чтобы вычислить интеграл функции f(x) = x 2 + 3 x — 4 на отрезке [5, 7],
нужно ввести integrate x^2 + 3x — 4, x=5..7
11. Вычисление пределов.
Пример . Чтобы убедиться, что
введите lim (x -> 0) (sin x)/x и посмотрите ответ. Если нужно вычислить какой-то предел при x, стремящемся к бесконечности, следует вводить x -> inf .
12. Исследование функции и построение графика .
Пример . Чтобы исследовать функцию x 3 — 3 x 2 и построить ее график, просто введите x^3-3x^2 . Вы получите корни (точки пересечения с осью ОХ), производную, график, неопределенный интеграл, экстремумы.
13. Нахождение наибольшего и наименьшего значений функции на отрезке .
Пример . Чтобы найти минимальное значение функции x 3 — 3 x 2 на отрезке [0.5, 2],
нужно ввести minimize (x^3-x^2),
Чтобы найти максимальное значение функции x 3 — 3 x 2 на отрезке [0.5, 2],
нужно ввести maximize (x^3-x^2),
- Как ввести систему уравнений в wolfram
- Основные операции
- Знаки сравнения
- Логические символы
- Основные константы
- Основные функции
- Решение уравнений
- Решение неравенств
- Решение различных систем уравнений, неравенств и уравнений
- Математический анализ
- Пределы
- Производные
- Интегралы
- Дифференциальные уравнения и их системы
- Ошибки при работе с системой
- Дифференциальные уравнения
- 📹 Видео
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как ввести систему уравнений в wolfram
Достаточно войти на страницу wolframalpha набрать в текстовом поле свой запрос и нажать на кнопку «=»
(имеет всплывающую подсказку вычислить ) или просто нажать Enter .
Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.
Например можно решить вот такое уравнение :
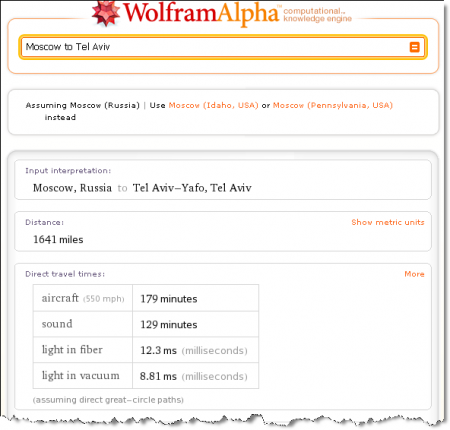
а чтобы узнать, какое расстояние между Москвой и Тель-Авивом, нужно ввести в поле
и вот вам результат:
Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы.
Основные команды для Вольфрам Альфа
(Команды вводятся в строку Вольфрама — например выше. Все команды заканчиваются нажатием Enter)
1. Решение уравнений, построение графиков
- Арифметические знаки плюс, минус, умножить, поделить +, — , *, / Примеры: 3*2, x*y, (a+b)/c
- Возведение в степень «x в степени а» x^a. Примеры x^a, x**a, (a+b)^2, (a+b)**2, (a+b)^(2x+1)
- Скобки. Действия в скобках ведутся первыми
- Функции .sin(x), cos(x), tan(x)=sin(x)/cos(x), cotan(x)=cos(x)/sin(x), sec(x)=1/cos(x), cosec(x)=1/sin(x)
- Функции log(x), exp(x), sinh(x), cosh(x), tanh(x), cotanh(x)
- Корень квадратный из «х» sqrt(x) или x^(1/2)
Чтобы вычислить выражение, нужно его просто ввести. Например корень из 2 будет выглядеть как sqrt(2) или же 2^(1/2).
2. Чтобы решить уравнение, нужно просто его ввести
3. Чтобы построить график, нужно использовать команду plot
Например нарисуем с помощью Вольфрама функцию 2^(-x) cos(x). Это делается командой plot (график).
Чтобы построить несколько графиков на одной координатной плоскости (например для визуализации решения систем уравнений), при значении переменной x в интервале (A,B), нужно использовать команду
4. Чтобы собрать множители из двучлена (многочлена) f, наберите factor[f]
5. Чтобы развалить произведение f на слагаемые, используйте команду expand[f]
6. Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Например упростить «е в степени догарифм х»:
Simplify[ exp[ log[x] ] ]
Вольфрам альфа: интегралы
Как работать с Wolfram Alpha
Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать

Основные операции
- Сложение
: a+b
- Вычитание
: a-b
- Умножение
: a*b
- Деление
: a/b
- Возведение в степень
: a^b
Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Видео:12.01 Решение систем ДУ в Wolfram MathematicaСкачать

Знаки сравнения
- Меньше
: : >
- Равно
: = или ==
- Меньше или равно
: =
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Логические символы
- И
: &&
- ИЛИ
: ||
- НЕ
: !
Видео:Rec 03 23 22 Решение систем уравнений с использованием Wolfram Д439Скачать

Основные константы
- Число
: Pi
- Число
: E
- Бесконечность
: Infinity, inf или oo
Видео:Видео курс Wolfram Mathematica | Лин. системы | Часть 1/2Скачать

Основные функции
: x^a
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]
Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Решение уравнений
Чтобы получить решение уравнения вида 
Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
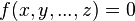

Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение неравенств
Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png» />, 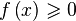

Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5 =9.
Видео:Математика это не ИсламСкачать

Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


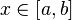


Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],].
Для того, чтобы построить график функции 
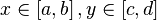


Видео:Система уравнений. Метод алгебраического сложенияСкачать

Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 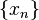
Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
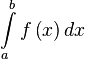
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 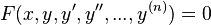
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: , где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.
Видео:Решение систем уравнений методом сложенияСкачать

Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач [1] . К примеру, если попытаться решить неравенство 
Видео:Решение систем уравнений методом подстановкиСкачать

Дифференциальные уравнения
Язык Wolfram позволяет решать обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и уравнения с запаздыванием.
Функция DSolveValue возвращает решение дифференциального уравнения в общем виде:
| Out[1]= | 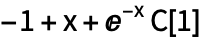 |
Используем символ /. для замены константы:
| Out[2]= | 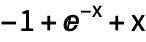 |
Или добавим начальные условия для получения частного решения:
| Out[3]= |  |
Функция NDSolveValue позволяет находить численные решения:
| Out[1]= |  |
Объект InterpolatingFunction можно визуализировать без дополнительной обработки:
| Out[2]= | 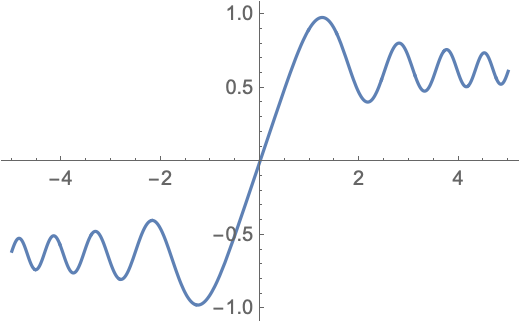 |
Для решения систем дифференциальных уравнений, необходимо использовать списки для задания уравнений и условий:
(Обратите внимание, что перенос уравнений на новую строку не влияет на результат.)
| Out[1]= | 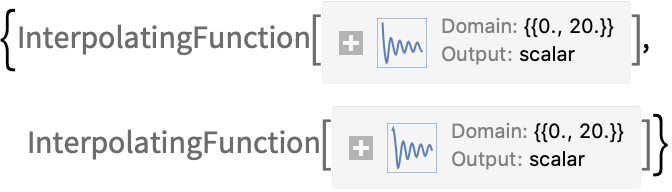 |
Построим решения системы в виде параметрического графика:
📹 Видео
9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

ФСР. Система однородных уравнений. Общее решениеСкачать

6 способов в одном видеоСкачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Матричный метод решения систем уравненийСкачать

Решение систем уравнений методом сложенияСкачать

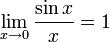

 : a+b
: a+b : a-b
: a-b : a*b
: a*b : a/b
: a/b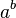 : a^b
: a^b : : >
: : > : = или ==
: = или == : =
: = : &&
: && : ||
: || : !
: ! : Pi
: Pi : E
: E : Infinity, inf или oo
: Infinity, inf или oo
 : x^a
: x^a : Sqrt[x]
: Sqrt[x] : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x] : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]