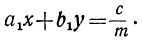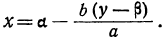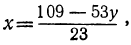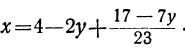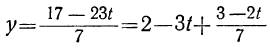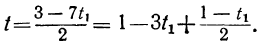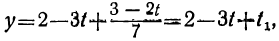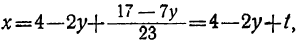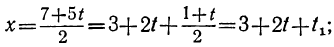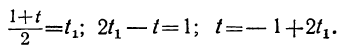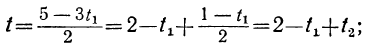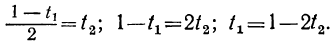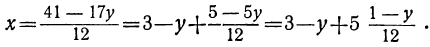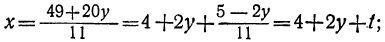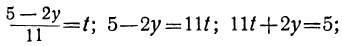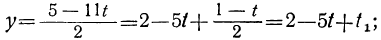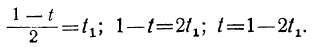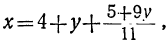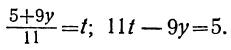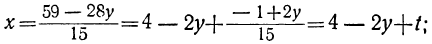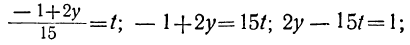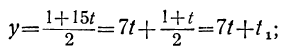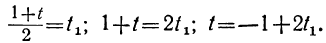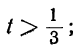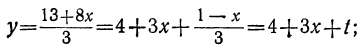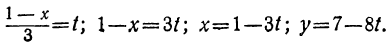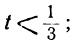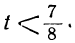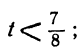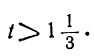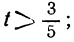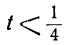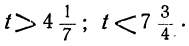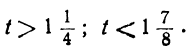Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.
- Какое уравнение не имеет корней?
- 1. Линейное уравнение
- 2. Квадратное уравнение
- 3. Тригонометрические уравнения
- 4. Системы уравнений
- Обобщение и советы по нахождению корней уравнения
- Решение простых линейных уравнений
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
- Неопределенные уравнения в математике с примерами решения и образцами выполнения
- Признак невозможности решения уравнения в целых числах
- Признак невозможности решения уравнения в положительных числах
- Общая формула корней неопределённого уравнения
- Способ подстановки
- Общее решение неопределённого уравнения
- Положительные решения
- 🔥 Видео
Видео:Доказать, что уравнение не имеет положительных корнейСкачать

Какое уравнение не имеет корней?
Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.
Сейчас мы рассмотрим самые базовые типы уравнений.
Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

1. Линейное уравнение
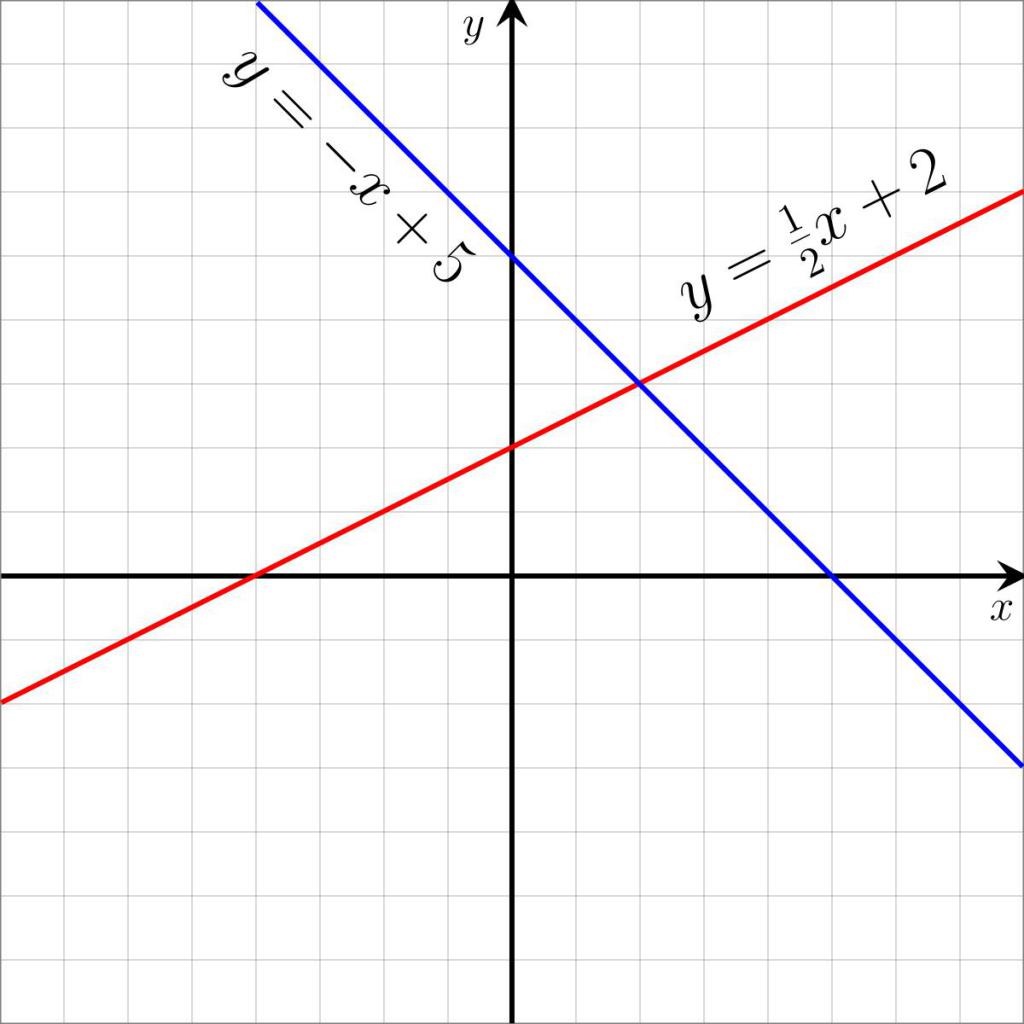
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.
В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.
Однако какое уравнение не имеет корней?
При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.
Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

2. Квадратное уравнение
Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х1,2= (-b ± √D) / 2 * a.
При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.
Видео:#75 Урок 36. Определение количества решений системы уравнений. Алгебра 7 класс.Скачать

3. Тригонометрические уравнения
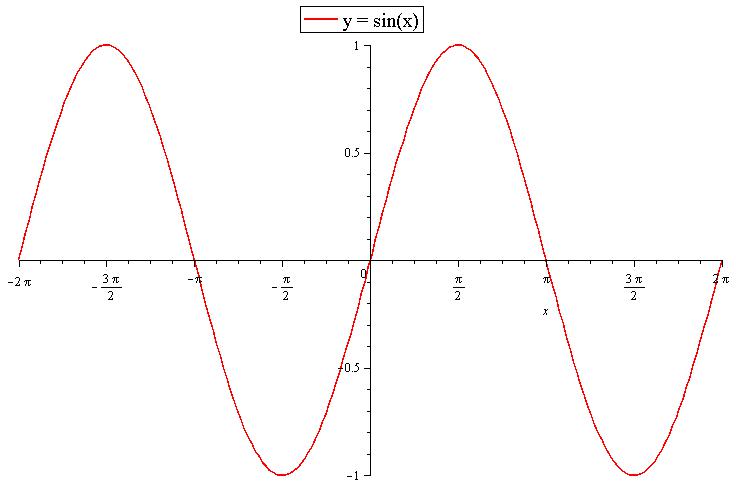
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.
Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.
Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.
Видео:Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

4. Системы уравнений
Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.
Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.
Видео:Показать, что уравнение x³+y³+z³=41 не имеет решений в целых числахСкачать

Обобщение и советы по нахождению корней уравнения
В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.
Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.
Итак, уравнение не имеет корней, если:
- в линейном уравнении mx = n значение m = 0 и n = 0;
- в квадратном уравнении, если дискриминант меньше нуля;
- в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
- в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Видео:Укажите неравенство, которое не имеет решений. | ОГЭ 2017 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРАСкачать

Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Видео:А ТЕПЕРЬ В КОЛЛЕДЖ! Все просто!Скачать

Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Видео:Вариант 40, № 2. Линейное уравнение, не имеющее корнейСкачать

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Неопределенные уравнения в математике с примерами решения и образцами выполнения
При изучении уравнений первой степени мы уже видели, что если число уравнений меньше числа неизвестных, то такая система имеет бесчисленное множество решений. Такие уравнения называются неопределёнными.
Наиболее часто в практике встречается случай одного уравнения с двумя неизвестными. Общий вид такого уравнения будет:
αx+by=c,
где x и у—неизвестные, а, b и с—данные коэффициенты.
Часто условия задачи бывают таковы, что правильный ответ на вопрос, поставленный в задаче, дают только целые значения, а иногда только целые и притом положительные значения.
Задача:
Разложить число 118 на такие два числа, из которых одно делилось бы на 11, а другое на 17.
Обозначая одно число через Их, а другое через 17у, мы получим уравнение:
11x+17y=118.
Так как в задаче ничего не сказано о знаке чисел, на которые нужно разложить число 118, то в данном случае мы можем считать ответом на задачу и отрицательные решения. Так, условию задачи удовлетворяют числа 33 и 85 (при х=3 и у=5), но также удовлетворяют и числа 220 и —102 (при х=20 и у=—6).
Задача:
Для упаковки самоваров имеются ящики, из которых в одни укладываются 4 самовара, в другие 7. Сколько нужно взять тех или других ящиков, чтобы упаковать 41 самовар?
Обозначив число малых ящиков через х, а число больших через у, будем иметь уравнение:
4x-+7y=41.
Очевидно, что по условию задачи здесь пригодны только целые и притом положительные решения. Такое решение данное уравнение допускает лишь одно, именно: x=5, у=3.
Таким образом, необходимо уметь решать неопределённые уравнения в целых числах, а также в целых и положительных числах.
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Признак невозможности решения уравнения в целых числах
Если среди коэффициентов а, b и с имеются дробные, то мы можем привести все коэффициенты к одному знаменателю и затем его отбросить. Тогда все коэффициенты будут целыми числами.
Далее, если а, b и с имеют какой-либо общий множитель, то на него можно сократить обе части уравнения.
Итак, мы будем предполагать, что коэффициенты a, b и с —числа целые, не имеющие общего множителя.
Предположим теперь, что а и b имеют общим множителем некоторое целое число, отличное от 1. Пусть, например,
a=ma₁, b=mb₁.
Разделив все его члены на m, получим:
При целых значениях х и у левая часть уравнения представляет собой целое число, правая же часть — дробь, так как с, по предположению, не делится на m. Такое равенство невозможно. Следовательно:
Если коэффициенты при неизвестных неопределённого уравнения имеют общий множитель, которого не имеет свободный член, то уравнение не может иметь целых решений.
Поэтому во всех дальнейших рассуждениях мы будем предполагать числа а и b взаимно простыми.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Признак невозможности решения уравнения в положительных числах
Пусть в уравнении ax+by=c коэффициенты а и b положительны, а свободный член с — отрицателен. Тогда при всяких положительных значениях х и у левая часть уравнения будет положительной, а правая останется отрицательной. Такое равенство невозможно.
Если коэффициенты а и b отрицательны, а с — положительно, то, умножив все члены уравнения на —1, мы сведём этот случай к предыдущему. Итак:
Если коэффициенты при неизвестных неопределённого уравнения имеют знаки, противоположные знаку свободного члена, то уравнение не имеет положительных решений.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Общая формула корней неопределённого уравнения
Предположим, что каким-либо способом (например, путём непосредственных проб) мы нашли одно целочисленное решение неопределённого уравнения:
ax+by=с.
Пусть это решение будет х=а и y=β. Подставляя значение x и у в данное уравнение, получим тождество:
a a+bβ =c.
Вычитая почленно это тождество из данного уравнения, получим:
α(x-α)+b(y-β)=0,
откуда:
ax=aa — b(y—β), или
Для того чтобы x было целым числом, необходимо и достаточно, чтобы выражение было целым числом (так как а—число
целое). Другими словами, необходимо и достаточно, чтобы выражение b(y-β) нацело делилось на а. Но, по предположению, b — число взаимно простое с а, следовательно, необходимо (и достаточно), чтобы разность у—β нацело делилась на а. Обозначив целое частное от деления у— β на а через t (оно может быть и положительным и отрицательным), получим:
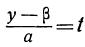
Подставляя в формулу для х число t вместо дроби 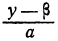
x = a-bt.
Таким образом, мы имеем для корней неопределённого уравнения формулы:
x = a-bt, y=β+at.
Давая в этих формулах t произвольные целые значения, положительные и отрицательные, мы получим бесчисленное множество целых решений данного неопределённого уравнения. В частности, при t=0 получим решение х = а; y=β, найденное нами уже ранее.
Присматриваясь к найденным формулам, легко заметить, что они составлены по следующему правилу:
- Первым членом формулы является найденное частное значение данного неизвестного.
- Вторым членом формул является произвольное целое число t, умноженное на коэффициент данного уравнения, причём в формуле для x берётся коэффициент при у в данном уравнении, а в формуле для у берётся коэффициент при х.
- Один из коэффициентов берётся с обратным знаком.
Нетрудно видеть, что совершенно безразлично, который из коэффициентов мы берём с тем же знаком, с каким он стоит в уравнении и который берём с обратным знаком. В самом деле, формулы:
x=a-bt, y=β+at и x=a+bt, y=β -at
будут давать одни и те же решения; только те решения, которые одни формулы дают при положительных значениях t, другие будут давать при равных по абсолютной величине отрицательных значениях t.
Пример:
Непосредственной подстановкой убеждаемся, что уравнение удовлетворяется значениями х=2 и у=4. Тогда все остальные решения найдутся из формул:
x=2+5t, у=4—3t, или х=2—5t, y=4+3t.
Давая в этих формулах t произвольные целые значения, будем получать различные целочисленные решения данного уравнения. Например, взяв первые формулы, будем иметь:
| t | 0 | 1 | 2 | 3 | -1 | -2 | … |
| x | 2 | 7 | 12 | 17 | -3 | -8 | … |
| y | 4 | 1 | -2 | -5 | 7 | 10 | … |
Если бы мы взяли вторые формулы, то те же решения получили бы, давая t последовательно значения: 0; —1; —2; —3; 1; 2 и т. д.
Таким образом, задача решения в целых числах неопределенного уравнения сводится к нахождению какого-либо одного решения.
Способ подстановки
Для нахождения одного решения неопределённого уравнения можно пользоваться следующим способом. Пусть дано уравнение:
ах+by=с.
Определим из него одно из неизвестных в зависимости от другого (лучше взять то, у которого коэффициент меньше). Пусть, например, a Частный вид неопределённого уравнения
Неопределённое уравнение легко решается в общем виде, когда один из коэффициентов при неизвестных равен единице. Пусть, например, равен единице коэффициент при х. Будем иметь:
x+by=c.
Определим х:
x=c-by.
Очевидно, что любому целому значению у будет соответствовать целое же значение х.
Пример:
Дано уравнение: 5x+y=18.
Находим:
у = 18—5х.
Давая x произвольные целые значения, будем соответственно получать целые значения для у:
| x | 0 | 1 | 2 | 3 | 4 | -1 | -2 | … |
| y | 18 | 13 | 8 | 3 | -2 | 23 | 28 | … |
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Общее решение неопределённого уравнения
Покажем на примере способ решения неопределённого уравнения с любыми коэффициентами. Пусть дано уравнение:
23x+53y=109.
Определим из этого уравнения то неизвестное, у которого коэффициент меньше, в данном случае х:
или, исключив целую часть:
Для того чтобы x было целым при у целом, необходимо и достаточно, чтобы выражение 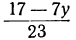
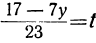
Если мы найдём для у и t такие целые значения, которые удовлетворяют уравнению 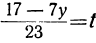
23t+7y=17,
то тем самым мы найдём соответствующие целые значения для х, и наша задача будет решена. Таким образом, решение данного уравнения мы свели к решению другого, более простого уравнения, у которого коэффициенты меньше, чем у данного.
По отношению к новому уравнению поступаем таким же образом. Определяем из него у:
Для того чтобы у было целым, необходимо и достаточно, чтобы 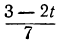
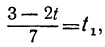
При целых t и t₁, удовлетворяющих последнему уравнению, мы получим соответственно целые значения для х и у, удовлетворяющие данному уравнению. Следовательно, наша задача свелась к решению последнего уравнения, у которого коэффициенты ещё меньше. Поступаем с ним так же, как и прежде:
Приравняв выражение 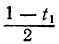
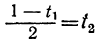
Мы получили уравнение, в котором коэффициент при одном из неизвестных равен единице, а такие уравнения решать мы уже умеем. Решив его, получим:
t₁=1-2t₂.
Давая в этом уравнении произвольные целые значения t₂, будем получать целые значения для t₁. Подставляя найденные целые значения t₁ и t₂ в выражение для t: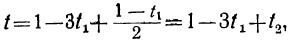
получим соответствующие целые значения для t. Подставляя соответствующие пары значений t и t₁ в выражение для у:
получим соответствующие целые значения для у. Наконец, делая подстановку найденных значений для у и t в выражение для х:
получим соответствующие целые значения для х.
Можно, однако, прямо выразить х и у в зависимости от t₂. Для этого подставим в выражение для t вместо t₁ его выражение через t₂:
t=1-3t₂+t₂=1-3 (1—2t₂)+t₂ ,
или
t=-2+7t₂ .
Подставим теперь в выражение для у вместо t и t₁ их выражения через t₂:
y=2-3t+t₁=2-3(-2+7t₂) + (1- 2t₂),
или
y=9-23t₂.
Наконец, подставляя найденные значения у и t в выражение для х, получим:
x=4-2y+t=4-2(9-23t₂)+(-2+7t₂),
или
x=- 16+53t₂ .
Таким образом, мы получим для х и у формулы:
x= — 16+53t₂, y=9-23t₂.
Давая в них произвольные целые значения для t₂, как положительные, так и отрицательные, будем получать бесчисленное множество решений данного уравнения; некоторые из них помещены в следующей таблице:
| t₂ | 0 | 1 | 2 | -1 | -2 |
| x | -16 | 37 | 90 | -69 | -122 |
| y | 9 | -14 | -37 | 32 | 55 |
Рассматривая операции, которые производились над коэффициентами данного и следующих уравнений, можно заметить такую последовательность:
- Больший коэффициент данного уравнения 53 делили на меньший 23; получили частное 2 и остаток 7.
- Меньший коэффициент данного уравнения 23 делили на остаток 7; получили частное 3 и второй остаток 2.
- Первый остаток 7 делили на второй остаток 2; получили частное 3 и третий остаток 1.
Другими словами, мы поступали точно так, как если бы находили общий наибольший делитель коэффициентов данного уравнения.
Мы знаем, что два взаимно простых числа имеют общим наибольшим делителем единицу. А так как в неопределённом уравнении мы всегда предполагаем коэффициенты при неизвестных взаимно простыми, то производя над уравнением указанные выше операции, мы всегда придём к такому уравнению, у которого коэффициент при одном из неизвестных равен единице. Тем самым мы находим решения и данного уравнения. Отсюда следует:
Если коэффициенты при неизвестных неопределённого уравнения-числа взаимно простые, то уравнение всегда имеет целые решения.
Упрощение решения уравнения. Иногда при решении неопределённого уравнения можно внести некоторые упрощения, позволяющие быстрее прийти к решению.
1. В случае, когда один из коэффициентов при неизвестных и свободный член имеют общий множитель, то на него можно сократить обе части уравнения, если надлежащим образом ввести новое неизвестное.
Пример:
Коэффициент 6 и свободный член имеют общим множителем 3. Следовательно, и член 5у должен делиться на 3, а так как 5 не делится на 3, то у должен быть кратным трём. Полагая у=3t, где t— целое число, будем иметь:
6x-15t=21,
или, по сокращении на 3:
2x-5t =7.
Решаем последнее уравнение:
Подставляя найденное значение в выражения, полученные для х и у, будем иметь:
x=3+2(-1+2t₁)+t₁ =1+5t₁;
y=3(-1+2t₁) = -3+6t₁ .
Пример:
Дано уравнение: 9x+14y=105.
Полагая у=3t и сокращая обе части уравнения на 3, получим:
3x+14t=35.
Полагая в этом уравнении x=7t₁ и сокращая обе части уравнения на 7, получим:
3t₁ +2t=5.
Решаем последнее уравнение:
Произведя последовательные подстановки, получим:
t=2-(1-2t₂) + t₂ = 1+3t₂;
x=7t₁=7(1-2t₂)=7-14t₂ ;
y=3t=3(1+3t₂) = 3+9t₂ .
2. Если в приравниваемом целому числу выражении члены, находящиеся в числителе, имеют общий множитель, то решение уравнения можно упростить.
Пример:
Дано уравнение: 12x+17y=41.
Решаем его относительно х:
Для того чтобы выражение 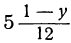
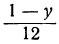
Приравнивая это выражение целому числу t, получим: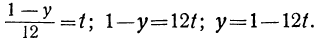
Соответственно получаем для х:
x=3-(1-12t)+5t=2+17t
3. Если при выделении целой части остаток будет более половины делителя, то удобно ввести отрицательный остаток.
Пример:
Дано уравнение: 11х—20y=49.
Решим его относительно х:
Произведя подстановки, получим:
y=2-5(1-2t₁)+t₁ = -3+11t₁;
x=4+2(-3+ 11t₁)+(1-2t₁) = -1+20t₁.
Если бы решали данное уравнение обычным способом, то получили бы для х:
и следующее уравнение было бы:
Это уравнение сложнее уравнения, полученного нами при помощи введения отрицательного остатка:
11t+2y=5.
Пример:
Дано уравнение: 15x+28y=59.
Решаем уравнение относительно х, вводя отрицательные остатки:
Попробовав решить приведённые в примерах уравнения обычным путём, легко убедимся, что без применения указанных упрощений все они потребовали бы для решения большего числа операций.
Положительные решения
Как уже говорилось ранее, часто из всех найденных решений неопределённого уравнения нужно взять лишь те, которые дают одновременно положительные значения для х и у. Найдя общие формулы для х и у, можно сразу определить, при каких значениях произвольного множителя будут получаться целые и положительные значения х и у.
Для того чтобы x и у были положительными, необходимо брать для t только такие значения, при которых:
a+bt>0; β-αt>0.
Будем считать а числом положительным. (Это мы всегда имеем право предположить, так как в противном случае мы могли бы обе части уравнения умножить на —1.) Тогда могут встретиться три различных случая.
1. Оба неравенства одинакового смысла. Это случится когда b — число отрицательное. В самом деле, пользуясь свойствами неравенства, будем иметь:
bt > — a ; at 0; 2+-5t>0,
или
Взяв для t любое целое число, большее 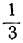
Пример:
Решаем уравнение:
Ищем положительные решения:
1 —3t>0; 7 —8t>0,
или
Любое целое значение t, меньшее 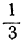
2. Неравенства противоположного смысла, причём они противоречат одно другому. Пусть, например, мы получим следующие неравенства:
Очевидно, что не существует таких значений t, которые одновременно удовлетворяли бы обоим неравенствам. В этом случае уравнение не может иметь положительных решений.
Пример:
4x+5y=-7.
Решая это уравнение, получим:
х=— 3+5t; y=1—4t.
Отсюда:
— 3+5t>0; 1 — 4t>0,
или
Неравенства противоречат друг другу; уравнение не имеет положительных решений.
3. Неравенства противоположного смысла, причём они не противоречат друг другу. Пусть, например, мы получили неравенства:
Все целые значения t, заключающиеся между 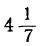
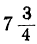
6 и 7, дадут для х и у положительные решения. Таким образом, в этом случае:
Уравнение имеет столько целых положительных решений, сколько целых чисел заключено между найденными пределами для t.
Заметим, что, в частности, уравнение и здесь может не иметь положительных решений. Это будет тогда, когда между найденными пределами для t не содержится ни одного целого числа. Например, пусть мы получим неравенства:
Неравенства не противоречат друг другу, но между 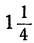
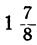
находится ни одного целого числа. Уравнение не имеет целых положительных решений.
Пример:
3x+7y=55.
Решаем уравнение: 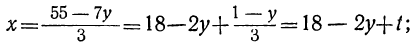
у=1 — 3t; x= 16+7t.
Отсюда:
1 —3t>0; 16+7t> 0,
или
Очевидно, для / можно взять лишь значения: 0; —1; —2. Получаем три решения уравнения:
| t | 0 | -1 | -2 |
| x | 16 | 9 | 2 |
| y | 1 | 4 | 7 |
Пример:
5. 5x+4y=3.
Решая уравнение, получим:
х=— 1 + 4t; у=2 —5t.
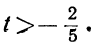
Отсюда:
Неравенства не противоречат друг другу; но между 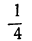
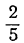
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔥 Видео
Исследование систем линейных уравнений на совместностьСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Как решают уравнения в России и СШАСкачать