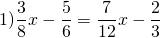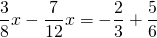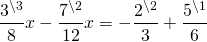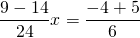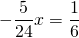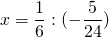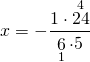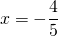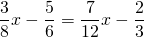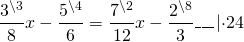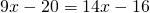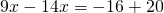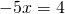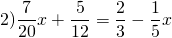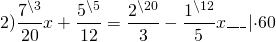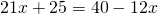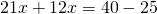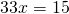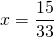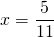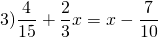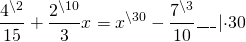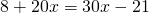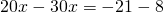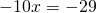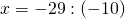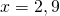Как упростить уравнение с дробью

Видео:Алгебраические дроби|как упростить выражение?Скачать

Упрощения алгебраических выражений

Видео:94 Алгебра 8 класс, упростите выражение, сложение и вычитание дробей, рациональные дроби, дробьСкачать

Что значит упростить алгебраическое выражение

Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).

Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.

Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.

Видео:Действия с алгебраическими дробями | Математика | TutorOnlineСкачать

Правила упрощения алгебраических выражений

Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:

• приведение подобных;
• разложение на множители;
• сокращение дроби;
• сложение и вычитание дробей;
• умножение и деление дробей.

В процессе приведения выражения в более простую форму следует использовать полезные советы:

1. При наличии подобных их рекомендуется привести, при этом не имеет значения то, в какой момент они образовались.
2. При появлении первой возможности для сокращения дробей, рекомендуется ей сразу воспользоваться. Исключением являются дроби с одинаковыми знаменателями, которые требуется вычитать или суммировать. Такие дроби можно сократить после выполнения необходимых действий.

Приведение подобных

Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.

Подобными являются слагаемые (одночлены), которые обладают буквенной частью.

В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.

Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.

К примеру, приведем слагаемые:

2 a + 3 b — a + 8 b + 7 a = 8 a + 11 b

Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.

Рассмотрим выражение с квадратной степенью:

Здесь число 3 является коэффициентом.

Разложение на множители

Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.

a b 2 + a 2 c = a b 2 + a c

4 x 2 — 16 x y + 16 y 2 = 4 x 2 — 4 x y + 4 y 2 = 4 x — 2 y 2

В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.

Сокращение дроби

В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.

Объяснение алгоритм действий при сокращении дробей:

• разложение на множители числителя и знаменателя;
• при наличии в числителе и знаменателе общих множителей их допустимо исключить из выражения.

Пример 5

a a + b a 2 = a a + b a · a = a + b a

Важно заметить, что сокращению подлежат исключительно множители.

Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.

Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».

Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.

Сложение и вычитание дробей

При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:

a b + c d = a · d + c · b b · d ;

a b — c d = a · d — c · b b · d

Разберем правило на конкретных примерах. Вычислим:

Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:

2 · 4 — 1 · 3 3 · 4 = 5 12

В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:

3 · 3 + 2 · 4 — 5 · 12 24 = — 43 24

В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:

3 4 7 — 1 2 3 = 25 · 3 7 — 5 · 7 3 = 75 — 35 21 = 40 21

Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:

• определить общий множитель;
• умножить каждую дробь на недостающий множитель;
• сложить или вычесть числители.

Здесь общий множитель равен 12. Тогда:

a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12

Далее можно привести подобные в числители, и разложить на множители при их наличии:

a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12

Когда знаменатели содержат буквы, схема действий существенно не меняется:

• разложение знаменателей на множители;
• определение одинаковых множителей;
• выделение всех общих множителей по одному разу;
• умножение общих множителей на оставшиеся множители, которые не являются общими.

Пример 7

Рассмотрим пример, когда требуется упростить выражение:

1 a b 2 + 1 a 2 b

Разложим знаменатели на множители:

a b 2 = a · b · b a 2 b = a · a · b

Вычислим единые множители:

a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯

Затем можно записать общие множители и выполнить умножение:

a ¯ · b ¯ ¯ · a · b = a 2 b 2

Общим знаменателем является a 2 b 2 . Умножим первую дробь на а, вторую — на b:

1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2

Умножение и деление дробей

Умножение и деление дробей выполняют таким образом:

a b · c d = a · c b · d ;

a b : c d = a · d b · c

Арифметические действия выполняют в следующем порядке:

• вычисление степени;
• умножение и деление;
• сложение и вычитание.

Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.

2 + 3 2 — 16 2 1 — 8 5 3 3

Используя правило умножения и деления дробей, получим:

2 + 3 2 — 16 2 1 — 8 5 3 3 = 2 + 9 — 16 2 1 — 8 5 3 3 = — 5 2 1 — 8 5 3 3 = 25 · 1 — 8 5 3 3 = 25 · — 3 5 3 3 = 25 5 · — 3 5 3 3 = 5 · — 3 3 3 = 5 · — 1 3 = — 5 3 = — 125

Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.

Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.

Попробуем упростить выражение:

x y — y x · 5 x y x + y

Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:

x · x y — y · y x = x · x — y · y y x = x 2 — y 2 y x = x — y x + y y x

Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:

x y — y x · 5 x y x + y = x — y x + y y x · 5 x y x + y

x — y x + y y x · 5 x y x + y = x — y x + y · 5 x y y x x + y

x — y x + y · 5 x y y x x + y = 5 x — y

Видео:Преобразование рациональных выражений. Тренировка. Алгебра 8 классСкачать

Пояснения на примерах

Требуется упростить выражения:

a — 2 b + 3 b + 6 a ;

a + a b — 3 a + 2 b a ;

a 2 b + a b 2 — a b + 2 a b 2 .

Приведем подобные и упростим выражения:

a ¯ — 2 b ¯ ¯ + 3 b ¯ ¯ + 6 a ¯ = 7 a + b

a ¯ + a b ¯ ¯ — 3 a ¯ + 2 b a ¯ ¯ = — 2 a + 3 a b

Заметим, что ab и 2ba являются подобными по той причине, что:

В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.

a 2 b + a b 2 ¯ — a b + 2 a b 2 ¯ = a 2 b + 3 ¯ a b 2 ¯ — a b .

Требуется упростить выражения:

a 3 b 4 — 3 a b 2 + 8 a 2 b 3

4 x 2 — 16 x y + 16 y 2

a 2 + 6 a y + 9 y 2 — 4

Путем разложения на множители упростим данные выражения:

a b 2 + a 2 c = a b 2 + a c

a 3 b 4 — 3 a b 2 + 8 a 2 b 3 = a b 2 a 2 b 2 — 3 + 8 a b

4 x 2 — 16 x y + 16 y 2 = 4 x 2 — 4 x y + 4 y 2 = 4 x — 2 y 2

a 2 + 6 a y + 9 y 2 — 4 = a + 3 y 2 — 2 2 = a + 3 y — 2 a + 3 y + 2

a 2 — b 2 a 2 + 2 a b + b 2

72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5

a a + b a 2 = a a + b a · a = a + b a

a 2 — b 2 a 2 + 2 a b + b 2 = a — b a + b a + b 2 = a — b a + b a + b a + b = a — b a + b

x 2 + 2 x y + y 2 x 2 — y 2

x 2 y — 4 y x 2 — 4 x + 4

a 3 — b 3 a 2 + a b + b 2

x 2 — 1 x — 1 = x 2 x = x

В первую очередь выполним разложение на множители:

x 2 — 1 x — 1 = x — 1 x + 1 x — 1 = x + 1

x 2 + 2 x y + y 2 x 2 — y 2 = x + y 2 : x + y x — y x + y : x + y = x + y x — y

x 2 y — 4 y x 2 — 4 x + 4 = y x 2 — 4 x — 2 2 = y x — 2 x + 2 x — 2 2 = y x + 2 x — 2

a 3 — b 3 a 2 + a b + b 2 = a — b a 2 + a b + b 2 a 2 + a b + b 2 = a — b .

Дано выражение, которое требуется упростить:

1 x y — 2 x 2 — x 4 x 2 — y 2

В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:

1 x y — 2 x 2 — x 4 x 2 — y 2 = 1 x y — 2 x — x 2 x — y 2 x + y

Рассмотрим выражение на наличие общих множителей:

y — 2 x = — 2 x — y

1 x y — 2 x 2 — x 4 x 2 — y 2 = 1 x y — 2 x — x 2 x — y 2 x + y = = 1 x y — 2 x — x — y — 2 x 2 x + y = 1 x y — 2 x + x y — 2 x 2 x + y

Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:

1 x y — 2 x + x y — 2 x 2 x + y = 2 x + y + x 2 x y — 2 x 2 x + y = x 2 + 2 x + y x y 2 — 4 x 2

Ответ: x 2 + 2 x + y x y 2 — 4 x 2

x 8 — x 3 + 1 x 2 + 2 x + 4

Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:

x 8 — x 3 + 1 x 2 + 2 x + 4 = x 2 3 — x 3 + 1 x 2 + 2 x + 4

Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:

x 2 + 2 x + 4 = x 2 + 2 · x + 2 2

Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:

x 8 — x 3 + 1 x 2 + 2 x + 4 = x 2 3 — x 3 + 1 x 2 + 2 x + 4 = x 2 — x x 2 + 2 x + 4 + + 1 · 2 — x x 2 + 2 x + 4 = x + 2 — x 2 — x x 2 + 2 x + 4 = 2 8 — x 3

Требуется упростить выражения:

3 a + 1 4 + 2 a — 3 10

2 x 2 — 5 3 + 3 x + 2 2 — 2 x 2 — 2 x — 1 4

5 a b — 3 · 2 a b 15 = 5 a b — 6 a b 15 = — a b 15

5 3 a + 1 + 2 2 a — 3 20 = 15 a + 5 + 4 a — 6 20 = 19 a — 1 20

4 2 x 2 — 5 + 6 3 x + 2 — 3 2 x 2 — 2 x — 1 12 = = 8 x 2 ¯ — 20 ¯ ¯ + 18 x ¯ ¯ ¯ + 12 ¯ ¯ — 6 x 2 ¯ + 6 x ¯ ¯ ¯ + 3 ¯ ¯ 12 = 2 x 2 — 5 + 24 x 12

Дано выражение, которое требуется упростить:

1 a 2 x 2 b 3 y — 1 a x 3 b 2 y 4

При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:

a во второй степени;

x в третьей степени;

b в третьей степени;

y в четвертой степени.

В результате получим:

1 · x · y 3 a 2 x 2 b 3 y — 1 · a · b a x 3 b 2 y 4 = x y 3 — a b a 2 x 3 b 3 y 4

Ответ: x y 3 — a b a 2 x 3 b 3 y 4

Нужно упростить выражение:

t + 3 3 t — 1 + t + 3 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1

Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.

Выглядит этот алгоритм таким образом:

t + 3 3 t — 1 + t + 3 t + 1 ⏞ 1 : t 2 + 3 t 1 — 3 t ⏞ 2 + t 2 + 3 t + 1 ⏞ 3 .

t + 3 · t + 1 3 t — 1 + t + 3 · 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = = t + 3 t + 1 + t + 3 3 t — 1 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = = t 2 + 3 t + t + 3 + 3 t 2 + 9 t — t — 3 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 =

4 t 2 + 12 t 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = 4 t t + 3 3 t — 1 t + 1 : t t + 3 1 — 3 t + t 2 + 3 t + 1 = .

= 4 t t + 3 3 t — 1 t + 1 · 1 — 3 t t t + 3 + t 2 + 3 t + 1 = 4 t t + 3 · 1 — 3 t — 1 3 t — 1 t + 1 · t t + 3 + + t 2 + 3 t + 1 = — 4 t + 1 + t 2 + 3 t + 1 = — 4 + t 2 + 3 t + 1 = t 2 — 1 t + 1 = t — 1 t + 1 t + 1 = t — 1

Видео:Решить уравнение с дробями - Математика - 6 классСкачать

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:8 класс, 4 урок, Преобразование алгебраических выраженийСкачать

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Упрощение выражений ОГЭ задача 12#2 🔴Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:220 Алгебра 8 класс, Упростите выражение дробиСкачать

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Упрощение выражений. 5 класс.Скачать

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Видео:Дробные выражения - как решать (примеры), как упрощатьСкачать

Уравнения с дробями

Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами.

Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.

1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Приводим к общему знаменателю дроби в каждой части уравнения:

Это — простейшее линейное уравнение . Обе части уравнения делим на число, стоящее перед иксом:

При делении чисел с разными знаками получаем отрицательное число. По правилу деления дробей :

После сокращения имеем:

(В данном случае ответ можно записать и в виде десятичной дроби: х=-0,8).

Обе части уравнения умножим почленно на наименьший общий знаменатель всех входящих в него дробей, в данном случае он равен 24:

При умножении на знаменатель дроби сокращаются, в знаменателе остается единица, которую не пишем. От линейного уравнения с дробями перешли к линейному уравнению с целыми числами:

Неизвестные — в одну сторону, известные — в другую с противоположными знаками:

Обе части уравнения делим на число, стоящее перед иксом:

Как видите, второй способ существенно упрощает решение линейного уравнения с дробями.

Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей. Здесь он равен 60:

Вместо линейного уравнения с дробями получили линейное уравнение с целыми числами. Неизвестные переносим в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Сокращаем дробь на 3:

Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей:

В результате линейное уравнение с дробями заменили на линейное уравнение с целыми числами:

Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

В следующий раз рассмотрим линейные уравнения с смешанными дробями.

🔍 Видео

СМЕШАННЫЕ ДРОБИ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

133 Алгебра 8 класс, упростите выражение, Выполните деление дробей примеры решениеСкачать

Задание №1 "Упростить выражение" по теме "Умножение и сложение многочленов и одночленов". Алгебра 7Скачать

Упрощение выражений. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Упрощение алгебраических уравнений. Подготовка к экзаменам. 9 часть. 9 класс.Скачать