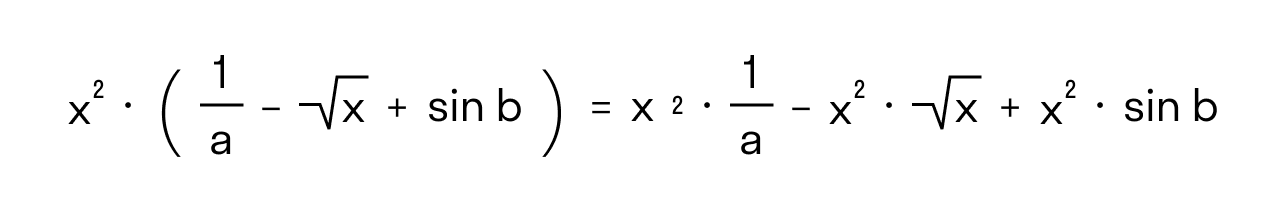Как упрощать уравнения со скобками

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Что значит упростить алгебраическое выражение

Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).

Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.

Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.

Видео:Упрощение выражений. 5 класс.Скачать

Правила упрощения алгебраических выражений

Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:

• приведение подобных;
• разложение на множители;
• сокращение дроби;
• сложение и вычитание дробей;
• умножение и деление дробей.

В процессе приведения выражения в более простую форму следует использовать полезные советы:

1. При наличии подобных их рекомендуется привести, при этом не имеет значения то, в какой момент они образовались.
2. При появлении первой возможности для сокращения дробей, рекомендуется ей сразу воспользоваться. Исключением являются дроби с одинаковыми знаменателями, которые требуется вычитать или суммировать. Такие дроби можно сократить после выполнения необходимых действий.

Приведение подобных

Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.

Подобными являются слагаемые (одночлены), которые обладают буквенной частью.

В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.

Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.

К примеру, приведем слагаемые:

2 a + 3 b — a + 8 b + 7 a = 8 a + 11 b

Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.

Рассмотрим выражение с квадратной степенью:

Здесь число 3 является коэффициентом.

Разложение на множители

Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.

a b 2 + a 2 c = a b 2 + a c

4 x 2 — 16 x y + 16 y 2 = 4 x 2 — 4 x y + 4 y 2 = 4 x — 2 y 2

В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.

Сокращение дроби

В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.

Объяснение алгоритм действий при сокращении дробей:

• разложение на множители числителя и знаменателя;
• при наличии в числителе и знаменателе общих множителей их допустимо исключить из выражения.

Пример 5

a a + b a 2 = a a + b a · a = a + b a

Важно заметить, что сокращению подлежат исключительно множители.

Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.

Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».

Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.

Сложение и вычитание дробей

При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:

a b + c d = a · d + c · b b · d ;

a b — c d = a · d — c · b b · d

Разберем правило на конкретных примерах. Вычислим:

Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:

2 · 4 — 1 · 3 3 · 4 = 5 12

В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:

3 · 3 + 2 · 4 — 5 · 12 24 = — 43 24

В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:

3 4 7 — 1 2 3 = 25 · 3 7 — 5 · 7 3 = 75 — 35 21 = 40 21

Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:

• определить общий множитель;
• умножить каждую дробь на недостающий множитель;
• сложить или вычесть числители.

Здесь общий множитель равен 12. Тогда:

a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12

Далее можно привести подобные в числители, и разложить на множители при их наличии:

a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12

Когда знаменатели содержат буквы, схема действий существенно не меняется:

• разложение знаменателей на множители;
• определение одинаковых множителей;
• выделение всех общих множителей по одному разу;
• умножение общих множителей на оставшиеся множители, которые не являются общими.

Пример 7

Рассмотрим пример, когда требуется упростить выражение:

1 a b 2 + 1 a 2 b

Разложим знаменатели на множители:

a b 2 = a · b · b a 2 b = a · a · b

Вычислим единые множители:

a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯

Затем можно записать общие множители и выполнить умножение:

a ¯ · b ¯ ¯ · a · b = a 2 b 2

Общим знаменателем является a 2 b 2 . Умножим первую дробь на а, вторую — на b:

1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2

Умножение и деление дробей

Умножение и деление дробей выполняют таким образом:

a b · c d = a · c b · d ;

a b : c d = a · d b · c

Арифметические действия выполняют в следующем порядке:

• вычисление степени;
• умножение и деление;
• сложение и вычитание.

Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.

2 + 3 2 — 16 2 1 — 8 5 3 3

Используя правило умножения и деления дробей, получим:

2 + 3 2 — 16 2 1 — 8 5 3 3 = 2 + 9 — 16 2 1 — 8 5 3 3 = — 5 2 1 — 8 5 3 3 = 25 · 1 — 8 5 3 3 = 25 · — 3 5 3 3 = 25 5 · — 3 5 3 3 = 5 · — 3 3 3 = 5 · — 1 3 = — 5 3 = — 125

Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.

Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.

Попробуем упростить выражение:

x y — y x · 5 x y x + y

Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:

x · x y — y · y x = x · x — y · y y x = x 2 — y 2 y x = x — y x + y y x

Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:

x y — y x · 5 x y x + y = x — y x + y y x · 5 x y x + y

x — y x + y y x · 5 x y x + y = x — y x + y · 5 x y y x x + y

x — y x + y · 5 x y y x x + y = 5 x — y

Видео:Раскрытие скобок. 6 класс.Скачать

Пояснения на примерах

Требуется упростить выражения:

a — 2 b + 3 b + 6 a ;

a + a b — 3 a + 2 b a ;

a 2 b + a b 2 — a b + 2 a b 2 .

Приведем подобные и упростим выражения:

a ¯ — 2 b ¯ ¯ + 3 b ¯ ¯ + 6 a ¯ = 7 a + b

a ¯ + a b ¯ ¯ — 3 a ¯ + 2 b a ¯ ¯ = — 2 a + 3 a b

Заметим, что ab и 2ba являются подобными по той причине, что:

В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.

a 2 b + a b 2 ¯ — a b + 2 a b 2 ¯ = a 2 b + 3 ¯ a b 2 ¯ — a b .

Требуется упростить выражения:

a 3 b 4 — 3 a b 2 + 8 a 2 b 3

4 x 2 — 16 x y + 16 y 2

a 2 + 6 a y + 9 y 2 — 4

Путем разложения на множители упростим данные выражения:

a b 2 + a 2 c = a b 2 + a c

a 3 b 4 — 3 a b 2 + 8 a 2 b 3 = a b 2 a 2 b 2 — 3 + 8 a b

4 x 2 — 16 x y + 16 y 2 = 4 x 2 — 4 x y + 4 y 2 = 4 x — 2 y 2

a 2 + 6 a y + 9 y 2 — 4 = a + 3 y 2 — 2 2 = a + 3 y — 2 a + 3 y + 2

a 2 — b 2 a 2 + 2 a b + b 2

72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5

a a + b a 2 = a a + b a · a = a + b a

a 2 — b 2 a 2 + 2 a b + b 2 = a — b a + b a + b 2 = a — b a + b a + b a + b = a — b a + b

x 2 + 2 x y + y 2 x 2 — y 2

x 2 y — 4 y x 2 — 4 x + 4

a 3 — b 3 a 2 + a b + b 2

x 2 — 1 x — 1 = x 2 x = x

В первую очередь выполним разложение на множители:

x 2 — 1 x — 1 = x — 1 x + 1 x — 1 = x + 1

x 2 + 2 x y + y 2 x 2 — y 2 = x + y 2 : x + y x — y x + y : x + y = x + y x — y

x 2 y — 4 y x 2 — 4 x + 4 = y x 2 — 4 x — 2 2 = y x — 2 x + 2 x — 2 2 = y x + 2 x — 2

a 3 — b 3 a 2 + a b + b 2 = a — b a 2 + a b + b 2 a 2 + a b + b 2 = a — b .

Дано выражение, которое требуется упростить:

1 x y — 2 x 2 — x 4 x 2 — y 2

В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:

1 x y — 2 x 2 — x 4 x 2 — y 2 = 1 x y — 2 x — x 2 x — y 2 x + y

Рассмотрим выражение на наличие общих множителей:

y — 2 x = — 2 x — y

1 x y — 2 x 2 — x 4 x 2 — y 2 = 1 x y — 2 x — x 2 x — y 2 x + y = = 1 x y — 2 x — x — y — 2 x 2 x + y = 1 x y — 2 x + x y — 2 x 2 x + y

Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:

1 x y — 2 x + x y — 2 x 2 x + y = 2 x + y + x 2 x y — 2 x 2 x + y = x 2 + 2 x + y x y 2 — 4 x 2

Ответ: x 2 + 2 x + y x y 2 — 4 x 2

x 8 — x 3 + 1 x 2 + 2 x + 4

Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:

x 8 — x 3 + 1 x 2 + 2 x + 4 = x 2 3 — x 3 + 1 x 2 + 2 x + 4

Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:

x 2 + 2 x + 4 = x 2 + 2 · x + 2 2

Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:

x 8 — x 3 + 1 x 2 + 2 x + 4 = x 2 3 — x 3 + 1 x 2 + 2 x + 4 = x 2 — x x 2 + 2 x + 4 + + 1 · 2 — x x 2 + 2 x + 4 = x + 2 — x 2 — x x 2 + 2 x + 4 = 2 8 — x 3

Требуется упростить выражения:

3 a + 1 4 + 2 a — 3 10

2 x 2 — 5 3 + 3 x + 2 2 — 2 x 2 — 2 x — 1 4

5 a b — 3 · 2 a b 15 = 5 a b — 6 a b 15 = — a b 15

5 3 a + 1 + 2 2 a — 3 20 = 15 a + 5 + 4 a — 6 20 = 19 a — 1 20

4 2 x 2 — 5 + 6 3 x + 2 — 3 2 x 2 — 2 x — 1 12 = = 8 x 2 ¯ — 20 ¯ ¯ + 18 x ¯ ¯ ¯ + 12 ¯ ¯ — 6 x 2 ¯ + 6 x ¯ ¯ ¯ + 3 ¯ ¯ 12 = 2 x 2 — 5 + 24 x 12

Дано выражение, которое требуется упростить:

1 a 2 x 2 b 3 y — 1 a x 3 b 2 y 4

При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:

a во второй степени;

x в третьей степени;

b в третьей степени;

y в четвертой степени.

В результате получим:

1 · x · y 3 a 2 x 2 b 3 y — 1 · a · b a x 3 b 2 y 4 = x y 3 — a b a 2 x 3 b 3 y 4

Ответ: x y 3 — a b a 2 x 3 b 3 y 4

Нужно упростить выражение:

t + 3 3 t — 1 + t + 3 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1

Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.

Выглядит этот алгоритм таким образом:

t + 3 3 t — 1 + t + 3 t + 1 ⏞ 1 : t 2 + 3 t 1 — 3 t ⏞ 2 + t 2 + 3 t + 1 ⏞ 3 .

t + 3 · t + 1 3 t — 1 + t + 3 · 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = = t + 3 t + 1 + t + 3 3 t — 1 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = = t 2 + 3 t + t + 3 + 3 t 2 + 9 t — t — 3 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 =

4 t 2 + 12 t 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = 4 t t + 3 3 t — 1 t + 1 : t t + 3 1 — 3 t + t 2 + 3 t + 1 = .

= 4 t t + 3 3 t — 1 t + 1 · 1 — 3 t t t + 3 + t 2 + 3 t + 1 = 4 t t + 3 · 1 — 3 t — 1 3 t — 1 t + 1 · t t + 3 + + t 2 + 3 t + 1 = — 4 t + 1 + t 2 + 3 t + 1 = — 4 + t 2 + 3 t + 1 = t 2 — 1 t + 1 = t — 1 t + 1 t + 1 = t — 1

Видео:Упрощение выражений. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Как упрощать уравнения со скобками

3.14159.. e Число e — основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности

Сервис (своего рода программа для классов 5 и 7, 8, 9, 10, 11) позволяет упрощать математические выражения: алгебра (алгебраические выражения), тригонометрических выражений, выражения с корнями и другими степенями, сокращение дробей, также упрощает сложные буквенные выражения,
для упрощение комплексных выражений вам сюда(!)

Важно В выражениях переменные обозначаются ОДНОЙ буквой! Например, a, b, . z

© Контрольная работа РУ — калькуляторы онлайн

Видео:КАК УПРОЩАТЬ ВЫРАЖЕНИЯ? · Раскрытие скобок · Упрощение выражений · Математика 6 классСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:КАК РАСКРЫТЬ СКОБКИ И УПРОСТИТЬ ВЫРАЖЕНИЕ? Примеры | МАТЕМАТИКА 5 классСкачать

Раскрытие скобок

О чем эта статья:

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

• знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
• произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

• 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1

Видео:КАК РАСКРЫТЬ СКОБКИ?Скачать

Первое правило раскрытия скобок

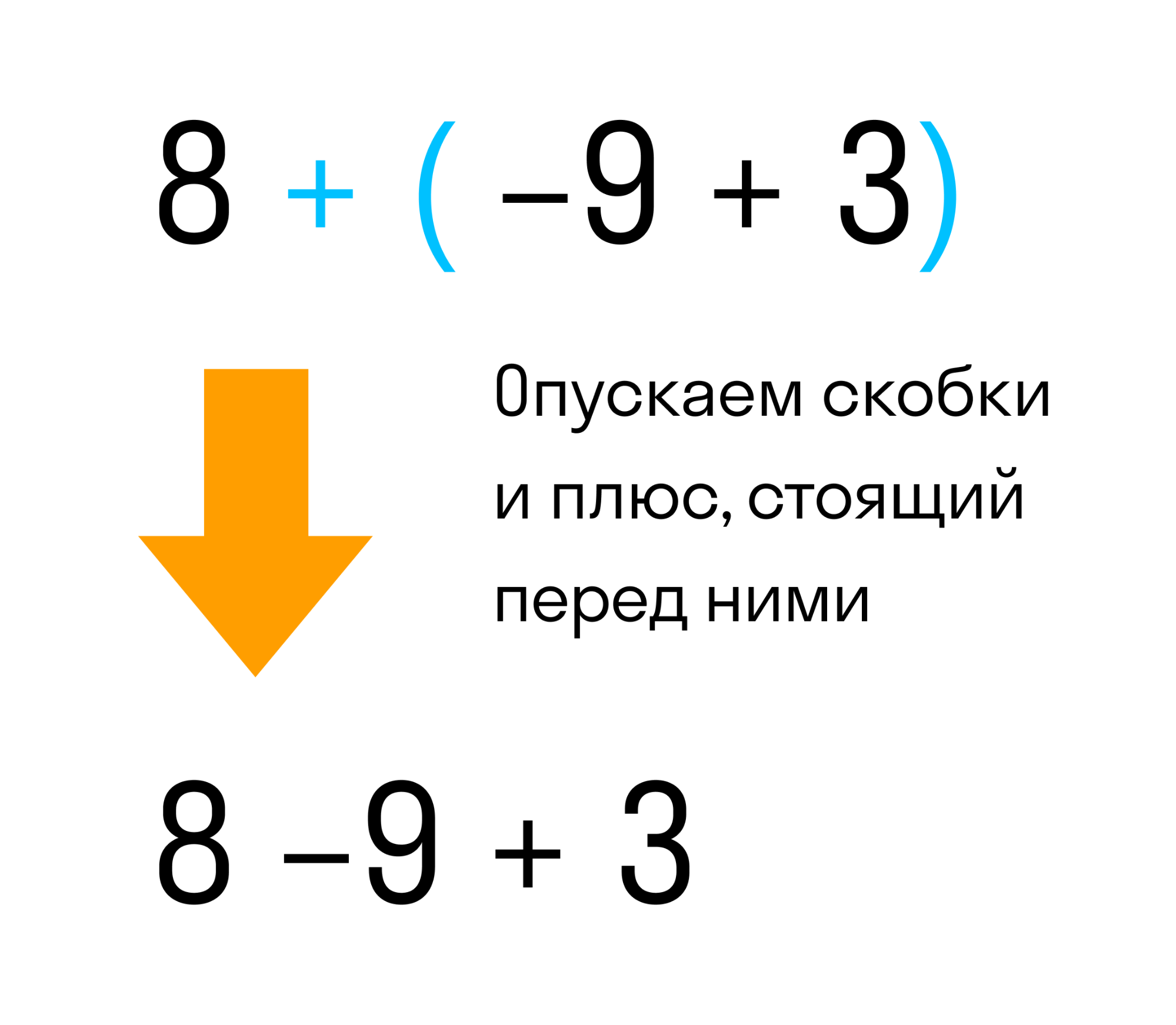
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

• 2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

• 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

• 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Упростите выражение используя свойства сложения. Математика 5 класс. (ошибки и как к ним относиться)Скачать

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

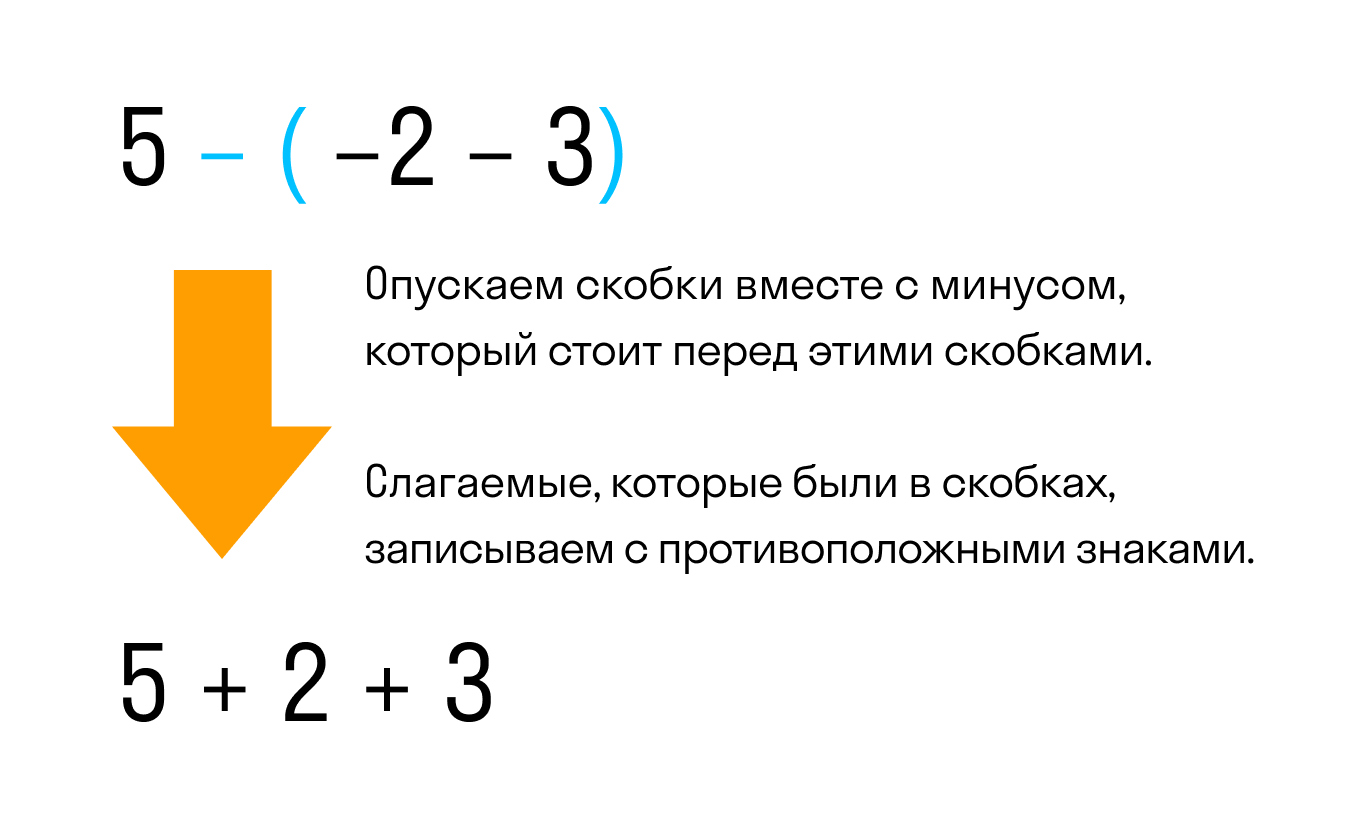
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

18 − (−1 − 5) = 18 + 1 + 5

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Видео:Уравнения со скобками - 5 класс (примеры)Скачать

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

(a + b) : c = a/c + b/c.

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

• (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Видео:КАК УПРОЩАТЬ СКОБКИ? · УПРОЩЕНИЕ ВЫРАЖЕНИЙ и ПОДОБНЫЕ СЛАГАЕМЫЕ · 5 класс Математика · ICAN SCHOOLСкачать

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

• перед скобкой стоит знак плюс:

a + (b — c + d) = a + b — c + d

• выражение начинается со скобки и перед ней нет знака:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

• перед скобкой стоит знак минус:

a — (b — c + d) = a — b + c — d

• выражение начинается с минуса перед скобкой:

-(a + b — c) + d = -a — b + c + d

Раскрытие круглых скобок при умножении одночлена на многочлен

a + b(c + d — f + e) = a + bc + bd — bf + be

a + b(c + d — f + e) = a + bc + bd — bf + be

-a(b + c — d) + f = -ab — ac + ad + f

Раскрытие круглых скобок при умножении многочлена на многочлен

(a + b)(c — d) = a(c — d) + b(c — d) = ac — ad + bc — bd

(-a + b)(c + d) = -a(c + d) + b(c + d)= -ac — ad + bc + bd

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Видео:5 класс, 14 урок, Упрощение выраженийСкачать

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

• упростить выражение 7x + 2(5 − (3 x + y)).

Чтобы успешно решать подобные задания, нужно:

• внимательно разобраться со скобками — какая в какой находится.
• раскрывать скобки последовательно, начиная с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y).

Теперь раскроем вторую скобку, внешнюю:

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y.

Упростим получившееся выражение:

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y = 7x + 10 − 6x − 2y.

• 7x + 10 − 6x − 2y = x + 10 − 2y

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

• возвести многочлены в скобках в натуральную степень;
• слева направо провести умножение и деление;
• когда в скобках останутся только слагаемые, раскрыть скобки и привести подобные.

Пример 1. Раскрыть скобки и упростить выражение:

-(2a + 5b) + (3a — 2b + 1) — (2a + 4) = -2a — 5b + 3a — 2b + 1 — 2a — 4 = (-2a + 3a — 2a) + (-5b — 2b) + (1 — 4) = -a — 7b — 3

Пример 2. Доказать, что при любых значениях переменной a значение выражения 3(2a — 7) — (a + (5a — 4)) — отрицательно.

33(2a — 7) — (a + (5a — 4)) = 3(2a — 7 ) — (a + 5a — 4)= 6a — 21 — a — 5a + 4 = (6a — a — 5a) + (-21 + 4) = -16/p>

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Видео:Упрощение буквенных выражений 5 класс.Скачать

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 1. Раскройте скобки в выражении: 2 + (6 + 3) + 2 — (1 + 1)

Задание 2. Раскройте скобки в выражении: — 21 + 14 + (-1 + 5) — 11 + ( 3 + 2)

Задание 3. Раскройте скобки в выражении: 3 * (-4m + 3n — 5)

Задание 4. Раскройте скобки в выражении: -(12a — 5b — 2)

Задание 5. Раскройте скобки в выражении: 3(x — 9)

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

💥 Видео

КАК РАСКРЫВАТЬ СКОБКИ? · Как умножать знаки? · Как упрощать выражения? · Математика 6 классСкачать

Булгакова О.А. (6 класс) Упрощение выражения (как раскрыть скобки)Скачать

Уравнения. 5 классСкачать

Упрощение выражения #математика #алгебра #упрощение #репетитор #репетиторматематикаСкачать

раскрытие скобок. Упрощение выражения.Скачать

Задание №1 "Упростить выражение" по теме "Умножение и сложение многочленов и одночленов". Алгебра 7Скачать