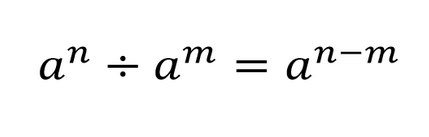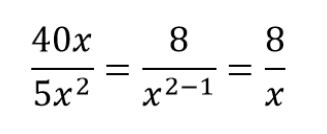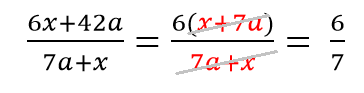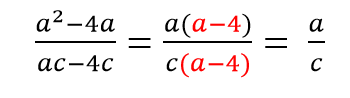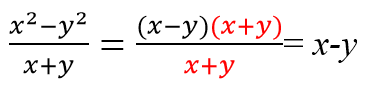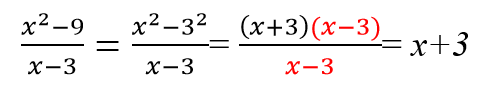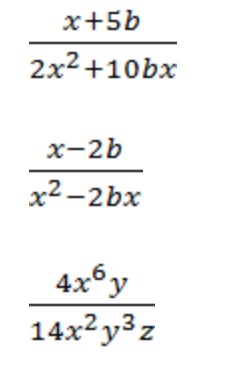О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Определение
- Сокращение алгебраических дробей
- Сокращение алгебраических дробей с многочленами
- Вынесение общего множителя при сокращении дробей
- Сокращение дробей. Формулы сокращенного умножения
- Решение дробных уравнений с преобразованием в квадратные уравнения
- Упрощения алгебраических выражений
- Что значит упростить алгебраическое выражение
- Правила упрощения алгебраических выражений
- Приведение подобных
- Разложение на множители
- Сокращение дроби
- Сложение и вычитание дробей
- Умножение и деление дробей
- Пояснения на примерах
- 💥 Видео
Видео:Алгебра 8. Урок 2 - Сокращение дробейСкачать

Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Видео:Сократить дробь алгебра 8 классСкачать

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
- Определите общий множитель.
- Сократите коэффициенты.
- Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
- Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
- Всегда делим на наименьшее значение в степени
- Вычитаем: 3 — 1
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
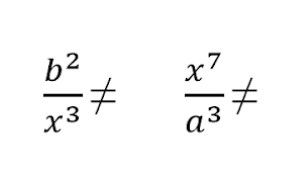 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
- Общий множитель для числителя и знаменателя — 8.
- Х и x 2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
- Общий множитель для числителя и знаменателя — 7.
- b 3 и b делим на b.
- Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Квадратный трехчлен . Сократить дробь.Скачать

Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
- сокращайте многочлен в скобках только с таким же многочленом в скобках;
- сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
| ❌ Так нельзя | ✅ Так можно |
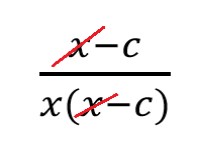 | 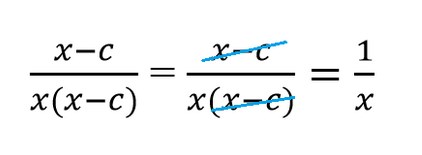 |
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
- Найдите число, на которое делятся числа каждого одночлена.
- Найдите повторяющиеся буквенные множители в каждом одночлене.
- Вынесите найденные буквенные множители за скобку.
- Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
- Выносим общий множитель 6
- Делим 42/6
- Сокращаем получившиеся одинаковые многочлены.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Видео:Действия с алгебраическими дробями | Математика | TutorOnlineСкачать

Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b) 2 = a 2 + 2ab + b 2 |
| Квадрат разности | (a-b) 2 = a 2 — 2ab — b 2 |
| Разность квадратов | a 2 – b 2 = (a – b)(a+b) |
| Куб суммы | (a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 |
| Куб разности | (a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 |
| Сумма кубов | a 3 + b 3 = (a + b)(a 2 — ab+b 2 ) |
| Разность кубов | a 3 — b 3 = (a — b)(a 2 + ab+b 2 ) |
Примеры сокращения дробей с помощью формул сокращенного умножения:
Применяем формулу квадрата разности (a-b) 2 = a 2 — 2ab — b 2 и сокращаем одинаковые многочлены.
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
- Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
- Поделите числитель и знаменатель на общий множитель.
- Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
- Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
- Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
- Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
- Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение 
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:

Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:

Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение

Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение


Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:

Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —

Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению


Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:

то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:

Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:

Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению


Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:

Решение. Введём новую переменную, обозначив 

Корни этого уравнения:


Из уравнения 

Из уравнения 

Итак, данное уравнение имеет четыре корня:


Видео:Алгебра 8. Урок 3 - Сложение и вычитание дробейСкачать

Упрощения алгебраических выражений
Видео:Преобразование выражений, содержащих кв. корни. Сокращение дробей. Практическая часть. 8 класс.Скачать

Что значит упростить алгебраическое выражение
Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).
Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.
Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.
Видео:Алгебра 8 класс с нуля | Математика ОГЭ 2023 | УмскулСкачать

Правила упрощения алгебраических выражений
Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:
- приведение подобных;
- разложение на множители;
- сокращение дроби;
- сложение и вычитание дробей;
- умножение и деление дробей.
В процессе приведения выражения в более простую форму следует использовать полезные советы:
- При наличии подобных их рекомендуется привести, при этом не имеет значения то, в какой момент они образовались.
- При появлении первой возможности для сокращения дробей, рекомендуется ей сразу воспользоваться. Исключением являются дроби с одинаковыми знаменателями, которые требуется вычитать или суммировать. Такие дроби можно сократить после выполнения необходимых действий.
Приведение подобных
Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.
Подобными являются слагаемые (одночлены), которые обладают буквенной частью.
В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.
Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.
К примеру, приведем слагаемые:
2 a + 3 b — a + 8 b + 7 a = 8 a + 11 b
Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.
Рассмотрим выражение с квадратной степенью:
Здесь число 3 является коэффициентом.
Разложение на множители
Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.
a b 2 + a 2 c = a b 2 + a c
4 x 2 — 16 x y + 16 y 2 = 4 x 2 — 4 x y + 4 y 2 = 4 x — 2 y 2
В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.
Сокращение дроби
В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.
Объяснение алгоритм действий при сокращении дробей:
- разложение на множители числителя и знаменателя;
- при наличии в числителе и знаменателе общих множителей их допустимо исключить из выражения.
Пример 5
a a + b a 2 = a a + b a · a = a + b a
Важно заметить, что сокращению подлежат исключительно множители.
Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.
Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».
Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.
Сложение и вычитание дробей
При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:
a b + c d = a · d + c · b b · d ;
a b — c d = a · d — c · b b · d
Разберем правило на конкретных примерах. Вычислим:
Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:
2 · 4 — 1 · 3 3 · 4 = 5 12
В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:
3 · 3 + 2 · 4 — 5 · 12 24 = — 43 24
В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:
3 4 7 — 1 2 3 = 25 · 3 7 — 5 · 7 3 = 75 — 35 21 = 40 21
Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:
- определить общий множитель;
- умножить каждую дробь на недостающий множитель;
- сложить или вычесть числители.
Здесь общий множитель равен 12. Тогда:
a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12
Далее можно привести подобные в числители, и разложить на множители при их наличии:
a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12
Когда знаменатели содержат буквы, схема действий существенно не меняется:
- разложение знаменателей на множители;
- определение одинаковых множителей;
- выделение всех общих множителей по одному разу;
- умножение общих множителей на оставшиеся множители, которые не являются общими.
Пример 7
Рассмотрим пример, когда требуется упростить выражение:
1 a b 2 + 1 a 2 b
Разложим знаменатели на множители:
a b 2 = a · b · b a 2 b = a · a · b
Вычислим единые множители:
a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯
Затем можно записать общие множители и выполнить умножение:
a ¯ · b ¯ ¯ · a · b = a 2 b 2
Общим знаменателем является a 2 b 2 . Умножим первую дробь на а, вторую — на b:
1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2
Умножение и деление дробей
Умножение и деление дробей выполняют таким образом:
a b · c d = a · c b · d ;
a b : c d = a · d b · c
Арифметические действия выполняют в следующем порядке:
- вычисление степени;
- умножение и деление;
- сложение и вычитание.
Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.
2 + 3 2 — 16 2 1 — 8 5 3 3
Используя правило умножения и деления дробей, получим:
2 + 3 2 — 16 2 1 — 8 5 3 3 = 2 + 9 — 16 2 1 — 8 5 3 3 = — 5 2 1 — 8 5 3 3 = 25 · 1 — 8 5 3 3 = 25 · — 3 5 3 3 = 25 5 · — 3 5 3 3 = 5 · — 3 3 3 = 5 · — 1 3 = — 5 3 = — 125
Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.
Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.
Попробуем упростить выражение:
x y — y x · 5 x y x + y
Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:
x · x y — y · y x = x · x — y · y y x = x 2 — y 2 y x = x — y x + y y x
Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:
x y — y x · 5 x y x + y = x — y x + y y x · 5 x y x + y
x — y x + y y x · 5 x y x + y = x — y x + y · 5 x y y x x + y
x — y x + y · 5 x y y x x + y = 5 x — y
Видео:Линейная функция, квадратичная функция и обратно-пропорциональная функция | Математика | TutorOnlineСкачать

Пояснения на примерах
Требуется упростить выражения:
a — 2 b + 3 b + 6 a ;
a + a b — 3 a + 2 b a ;
a 2 b + a b 2 — a b + 2 a b 2 .
Приведем подобные и упростим выражения:
a ¯ — 2 b ¯ ¯ + 3 b ¯ ¯ + 6 a ¯ = 7 a + b
a ¯ + a b ¯ ¯ — 3 a ¯ + 2 b a ¯ ¯ = — 2 a + 3 a b
Заметим, что ab и 2ba являются подобными по той причине, что:
В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.
a 2 b + a b 2 ¯ — a b + 2 a b 2 ¯ = a 2 b + 3 ¯ a b 2 ¯ — a b .
Требуется упростить выражения:
a 3 b 4 — 3 a b 2 + 8 a 2 b 3
4 x 2 — 16 x y + 16 y 2
a 2 + 6 a y + 9 y 2 — 4
Путем разложения на множители упростим данные выражения:
a b 2 + a 2 c = a b 2 + a c
a 3 b 4 — 3 a b 2 + 8 a 2 b 3 = a b 2 a 2 b 2 — 3 + 8 a b
4 x 2 — 16 x y + 16 y 2 = 4 x 2 — 4 x y + 4 y 2 = 4 x — 2 y 2
a 2 + 6 a y + 9 y 2 — 4 = a + 3 y 2 — 2 2 = a + 3 y — 2 a + 3 y + 2
a 2 — b 2 a 2 + 2 a b + b 2
72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5
a a + b a 2 = a a + b a · a = a + b a
a 2 — b 2 a 2 + 2 a b + b 2 = a — b a + b a + b 2 = a — b a + b a + b a + b = a — b a + b
x 2 + 2 x y + y 2 x 2 — y 2
x 2 y — 4 y x 2 — 4 x + 4
a 3 — b 3 a 2 + a b + b 2
x 2 — 1 x — 1 = x 2 x = x
В первую очередь выполним разложение на множители:
x 2 — 1 x — 1 = x — 1 x + 1 x — 1 = x + 1
x 2 + 2 x y + y 2 x 2 — y 2 = x + y 2 : x + y x — y x + y : x + y = x + y x — y
x 2 y — 4 y x 2 — 4 x + 4 = y x 2 — 4 x — 2 2 = y x — 2 x + 2 x — 2 2 = y x + 2 x — 2
a 3 — b 3 a 2 + a b + b 2 = a — b a 2 + a b + b 2 a 2 + a b + b 2 = a — b .
Дано выражение, которое требуется упростить:
1 x y — 2 x 2 — x 4 x 2 — y 2
В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:
1 x y — 2 x 2 — x 4 x 2 — y 2 = 1 x y — 2 x — x 2 x — y 2 x + y
Рассмотрим выражение на наличие общих множителей:
y — 2 x = — 2 x — y
1 x y — 2 x 2 — x 4 x 2 — y 2 = 1 x y — 2 x — x 2 x — y 2 x + y = = 1 x y — 2 x — x — y — 2 x 2 x + y = 1 x y — 2 x + x y — 2 x 2 x + y
Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:
1 x y — 2 x + x y — 2 x 2 x + y = 2 x + y + x 2 x y — 2 x 2 x + y = x 2 + 2 x + y x y 2 — 4 x 2
Ответ: x 2 + 2 x + y x y 2 — 4 x 2
x 8 — x 3 + 1 x 2 + 2 x + 4
Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:
x 8 — x 3 + 1 x 2 + 2 x + 4 = x 2 3 — x 3 + 1 x 2 + 2 x + 4
Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:
x 2 + 2 x + 4 = x 2 + 2 · x + 2 2
Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:
x 8 — x 3 + 1 x 2 + 2 x + 4 = x 2 3 — x 3 + 1 x 2 + 2 x + 4 = x 2 — x x 2 + 2 x + 4 + + 1 · 2 — x x 2 + 2 x + 4 = x + 2 — x 2 — x x 2 + 2 x + 4 = 2 8 — x 3
Требуется упростить выражения:
3 a + 1 4 + 2 a — 3 10
2 x 2 — 5 3 + 3 x + 2 2 — 2 x 2 — 2 x — 1 4
5 a b — 3 · 2 a b 15 = 5 a b — 6 a b 15 = — a b 15
5 3 a + 1 + 2 2 a — 3 20 = 15 a + 5 + 4 a — 6 20 = 19 a — 1 20
4 2 x 2 — 5 + 6 3 x + 2 — 3 2 x 2 — 2 x — 1 12 = = 8 x 2 ¯ — 20 ¯ ¯ + 18 x ¯ ¯ ¯ + 12 ¯ ¯ — 6 x 2 ¯ + 6 x ¯ ¯ ¯ + 3 ¯ ¯ 12 = 2 x 2 — 5 + 24 x 12
Дано выражение, которое требуется упростить:
1 a 2 x 2 b 3 y — 1 a x 3 b 2 y 4
При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:
a во второй степени;
x в третьей степени;
b в третьей степени;
y в четвертой степени.
В результате получим:
1 · x · y 3 a 2 x 2 b 3 y — 1 · a · b a x 3 b 2 y 4 = x y 3 — a b a 2 x 3 b 3 y 4
Ответ: x y 3 — a b a 2 x 3 b 3 y 4
Нужно упростить выражение:
t + 3 3 t — 1 + t + 3 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1
Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.
Выглядит этот алгоритм таким образом:
t + 3 3 t — 1 + t + 3 t + 1 ⏞ 1 : t 2 + 3 t 1 — 3 t ⏞ 2 + t 2 + 3 t + 1 ⏞ 3 .
t + 3 · t + 1 3 t — 1 + t + 3 · 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = = t + 3 t + 1 + t + 3 3 t — 1 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = = t 2 + 3 t + t + 3 + 3 t 2 + 9 t — t — 3 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 =
4 t 2 + 12 t 3 t — 1 t + 1 : t 2 + 3 t 1 — 3 t + t 2 + 3 t + 1 = 4 t t + 3 3 t — 1 t + 1 : t t + 3 1 — 3 t + t 2 + 3 t + 1 = .
= 4 t t + 3 3 t — 1 t + 1 · 1 — 3 t t t + 3 + t 2 + 3 t + 1 = 4 t t + 3 · 1 — 3 t — 1 3 t — 1 t + 1 · t t + 3 + + t 2 + 3 t + 1 = — 4 t + 1 + t 2 + 3 t + 1 = — 4 + t 2 + 3 t + 1 = t 2 — 1 t + 1 = t — 1 t + 1 t + 1 = t — 1
💥 Видео
Как решать дробно-рациональные уравнения? | МатематикаСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать

Разложение квадратного трехчлена на множители. 8 класс.Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Алгебра 8. Урок 7 - Квадратный корень. Упрощение выраженийСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать