- Тестирование онлайн
- Гармоническое колебание
- График гармонического колебания
- Уравнение гармонического колебания
- Изменение скорости и ускорения при гармоническом колебании
- Максимальные значения скорости и ускорения
- Как получить зависимости v(t) и a(t)
- Построение графиков гармонических колебаний
- Что такое гармонические колебания?
- Гармонические колебания
- теория по физике 🧲 колебания и волны
- Уравнение движения гармонических колебаний
- Период и частота гармонических колебаний
- Зависимость частоты и периода свободных колебаний от свойств системы
- Фаза колебаний
- Превращение энергии при гармонических колебаниях
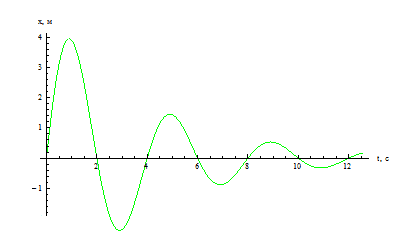
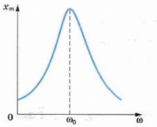
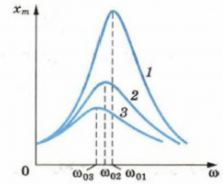
- Резонанс
- 🌟 Видео
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Тестирование онлайн
Видео:10 класс, 19 урок, График гармонического колебанияСкачать

Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
Видео:Урок 335. Анализ графика гармонических колебанийСкачать

График гармонического колебания
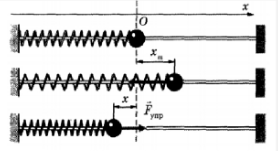
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

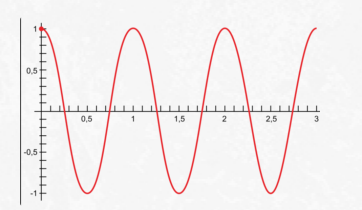
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Видео:Выполнялка 53.Гармонические колебания.Скачать

Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

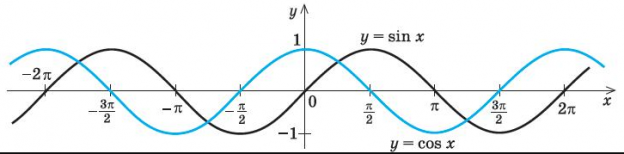
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Видео:Как построить график гармонического колебанияСкачать

Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Видео:Урок 327. Гармонические колебанияСкачать

Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Построение графиков гармонических колебаний
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Югорский государственный университет» (ЮГУ)
НИЖНЕВАРТОВСКИЙ НЕФТЯНОЙ ТЕХНИКУМ
(филиал) федерального государственного бюджетного образовательного учреждения
высшего профессионального образования «Югорский государственный университет»
(ННТ (филиал) ФГБОУ ВПО «ЮГУ»)
На заседании кафедры ЕиЭД
Зам. директора по учебной работе
ННТ (филиала) ФГБОУ ВПО «ЮГУ»
Методическая разработка занятия
« Построение графиков гармонических колебаний »
Преподаватель: Е.Н. Карсакова
Практическое занятие № 25
«Построение графиков гармонических колебаний »
Формирование навыков построения графиков гармонических колебаний;
Закрепление умений преобразования графиков функций;
Применение знаний к решению нестандартных задач по смежным дисциплинам;
Способствовать развитию алгоритмического и логического мышления;
Развитие точной, информативной речи;
Формирование навыков исследовательской работы;
Развитие творчества, инициативности;
Способствовать эстетическому восприятию графических изображений;
Воспитание умений действовать по заданному алгоритму;
Воспитание аккуратного, точного выполнения геометрических построений;
Тип занятия: формирование умений и навыков
Оборудование и материалы: МД проектор, карты с заданиями, тетради, линейки, карандаши.
Н.В. Богомолов « Практические занятия по математике», 2006г.
А.А. Дадаян « Математика», 2003г.
О.Н. Афанасьева, Я.С. Бродский « Математика для техникумов», 2001г
Объявление темы занятия; постановка целей;
Мотивация познавательной деятельности
Проверка опорных знаний
а) фронтальный опрос
Повторить виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях
Применение знаний к
изучению нового материала
Формирование умений и навыков построения графиков.
Построение графиков гармонических колебаний.
Закрепление умений и навыков построения графиков функций
Демонстрация лучших работ студентов.
Воспитание эстетического восприятия графических изображений;
Применение знаний к решению нестандартных задач
Показать связь математики с другими науками
Обобщение знаний, умений, навыков; оценка деятельности студентов
Инструктаж по домашнему заданию
Рождённый пустыней, колеблется звук,
Колеблется синий на нитке паук.
Колеблется воздух, прозрачен и чист,
В сияющих звездах колеблется лист.
Сообщение темы занятия; постановка целей; освещение основных этапов.
В технике и в окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать все колебательные процессы с единой точки зрения.
Механическими колебаниями называются периодические изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).
Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны . Примерами такого процесса являются звуковые волны в воздухе.
Как и колебания, волновые процессы различной физической природы (звук, электромагнитные волны, волны на поверхности жидкости и т. д.) имеют много общего. Распространение волн различной физической природы можно описывать с помощью одинаковых математических уравнений и функций. В этом проявляется единство материального мира.
Цель: Мотивация познавательной деятельности
Сегодня мы увидим, как с помощью математических законов и преобразований можно описывать некоторые физические явления. Например,
Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Что такое гармонические колебания?
Гармонические колебания – это периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса. Графиком гармонического колебания является синусоида или косинусоида , по которой можно определить все характеристики колебательного движения : амплитуду, период, частоту, начальную фазу .
Гармонические колебания играют важную роль в физике, электротехнике. Наша задача – построить графики гармонических колебаний, применив при этом все известные правила преобразований графиков без помощи трудоёмких вычислений и научиться описывать по ним колебательный процесс.
Гармонические колебания подчиняются следующему закону:
А — амплитуда, 

Период гармонических колебаний Т можно вычислить по формуле
Для построения графиков гармонических колебаний необходимо иметь чёткое представление о правилах построения графиков функций и их преобразованиях.
3. Проверка знаний учащихся по теме: «Преобразования графиков функций» (15 мин.)
Цель: Повторить основные виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях.
Задание 1. Сгруппируйте функции по общему признаку:
Рассмотрим подробно правила построения графиков функций с изменяющимся аргументом и меняющейся функцией. (Презентация.)
4. Изучение нового материала (20 мин.) (Презентация.)
Цель: Формирование умений и навыков исследования функции, построения графиков гармонических колебаний.
Задача 1. Построить график гармонических колебаний у = 2 sin (2 x — 
Сразу укажем на типовую ошибку в подобных задачах: осуществляют сдвиг на 


Как построить график такого колебания? Алгоритм построения следующий:
1. у = sinx — исходная функция .
2. у = sin 2 x — сжатие в 2 раза вдоль оси Ох.
3. у = 2 sin 2 x — растяжение в 2 раза вдоль оси Оу (рис. 1).
4. у = 2 sin 2( x — 

При построении данного графика были использованы следующие виды преобразования графиков:
Задача 2. Построить графики функций и определить основные характеристики гармонического колебания:
a ) у = sin 
a). Найдем период функции у = sin 
А=1;
Период колебания Т = 6 


А=1;
Построим график на участке длиной в период 

5. Построение графиков гармонических колебаний . Самостоятельная работа (30 мин).
Опыт – дитя мысли, мысль – дитя действий
Цель: Закрепление умений и навыков построения графиков функций
Построить графики гармонических колебаний:
y = cos
y = — sin ( x+ 
Критерии оценки деятельности учащихся:
(1-) – удовлетворительно; (1-2) – хорошо; (1-3) – отлично.
6. Демонстрация лучших работ студентов (3 мин).
Вдохновение нужно в математике, как и в поэзии.
Цель: Воспитание эстетического восприятия графических изображений;
7. Применение знаний к решению нестандартных задач (6 мин.)
Цель: Показать связь математики с другими науками;
Тело движется по закону у = cos 
Амплитуду колебаний А ;
Частоту колебаний
Период колебаний 
Начальную фазу
Ответ : А=1;
Дорогу осилит идущий, а математику – мыслящий.
Выполнение поставленных целей;
Приобретение навыков исследовательской работы;
Применение знаний к решению нестандартных задач;
Мы познакомились с графиками гармонических колебаний. Очевидно, что при их построении синусоида или косинусоида подверглись различным преобразованиям: сжатию, растяжению, сдвигу. Овладение этими правилами поможет при изучении других функций на последующих занятиях.
9. Домашнее задание (3 мин).
Построить график функции у = 3 cos (2 x + 
10. Это интересно!
Биение сердца также относится к колебательному процессу. В течение минуты оно выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови. Синусоидальные изменения ритмов сердца отражает кардиограф.
Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Гармонические колебания
теория по физике 🧲 колебания и волны
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
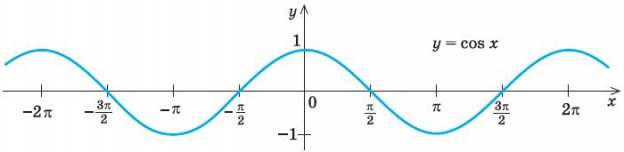
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Видео:5.4 Уравнение гармонических колебанийСкачать

Уравнение движения гармонических колебаний
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x″ = − x m a x cos . t = − x
Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x = x m a x cos . √ k m . . t
Тогда первая производная примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x′ = − √ k m . . x m a x sin . √ k m . . t
Вторая производная примет вид:
x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x = x m a x sin . √ k m . . t
x = x m a x cos . √ k m . . t
Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω0:
x = x m a x sin . ω 0 t
x = x m a x cos . ω 0 t
Само уравнение движения, описывающего свободные колебания, примет вид:
Видео:График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать

Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω 0 = 2 π T . . = 2 π ν
Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Видео:График гармонического колебанияСкачать

Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω 0 = √ k m . . = 2 π T . . = 2 π ν
Отсюда период и частота колебаний соответственно равны:
T = 2 π ω 0 . . = 2 π √ m k . .
ν = 1 2 π . . √ k m . .
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:
Отсюда период и частота колебаний математического маятника соответственно равны:
T = 2 π ω 0 . . = 2 π √ l g . .
ν = 1 2 π . . √ g l . .
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
Искомое число колебаний равно отношению времени к периоду колебаний:
Период колебаний для математического маятника определяется формулой:
N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:
ϕ = ω 0 t = 2 π t T . .
t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 |
| Фаза, ϕ (рад) | 0 |