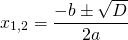- Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
- Решение квадратного уравнения на С# в Windows Forms.
- Решение квадратного уравнения
- Программа для решения квадратного уравнения на языке программирования Паскаль
- Программирование решения уравнений
- Скачать:
- Подписи к слайдам:
- Предварительный просмотр:
- Предварительный просмотр:
- Паспорт проекта
- Индивидуальный план работы над проектом
- Отзыв
- Общие сведения о языке программирования Паскаль
- Решение системы алгебраических уравнений методом Гаусса
- Решение нелинейных уравнений
- Заключение
- Список литературы
- Текст публичного выступления
- 🌟 Видео
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Видео:Уроки C++. Простые линейные уравненияСкачать

Решение квадратного уравнения на С# в Windows Forms.
Сегодня мы напишем программу, которая выведет нам решение квадратного уравнения на С#. Сделаем мы всё это в Windows Forms. В программе мы найдём дискриминант и оба корня.
Для создания программы нам понадобится знание начальной школы и трёх формул.
Формула нахождения дискриминанта:
Формула нахождения корней выражения, если дискриминант больше нуля:
И формула нахождения одного корня выражения, если дискриминант равен нулю:
Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:
Теперь пора приступать к программе.
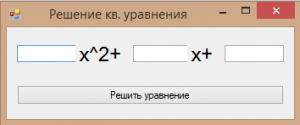
Для начала создаём незамысловатую форму под наши нужды:
Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.
Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.
Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:
Видео:Простая программа для решения кв.уравнения в VBСкачать

Решение квадратного уравнения
Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.
a, b, c — действительные числа, a ≠ 0.
Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.
- если D 0, то уравнение имеет два действительных корня:
- x1 = (-b + √D) / (2⋅a);
- x2 = (-b + √D) / (2⋅a).
Видео:Программа, определяющая корни квадратного уравнения. Язык программирования Python.Скачать

Программа для решения квадратного уравнения на языке программирования Паскаль
Функция sqr языка Pascal используется для возведения числа в квадрат.
Функция sqrt используется для получения квадратного корня числа.
В программе используется форматированный вывод вещественных чисел. variable:8:3 — означает, что для вывода переменной предусмотрено 8 символов, 5 из них под целую часть и 3 под дробную.
Видео:решаем квадратные уравнения в ExcelСкачать

Программирование решения уравнений
Программирование решения уравнений. Презентация, проект и программный продукт (программа в Pascal)
Видео:решение (поиск корней) квадратных уравнений c++Скачать

Скачать:
| Вложение | Размер |
|---|---|
| programmirovanie_lineynyh_uravneniy.pptx | 1.54 МБ |
| metod_nyutona.docx | 69.43 КБ |
| programmirovanie_resheniya_uravneniy.docx | 911.13 КБ |
Предварительный просмотр:
Видео:Квадратные уравнения: программирование на VBAСкачать

Подписи к слайдам:
Программирование линейных уравнений Работа ученика 9б класса Ф.И.О. обучающегося: Смолькова Андрея Владимировича Руководитель проекта Ф.И.О. Борисова О.А.
Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами . Язык Паскаль – универсальный язык программирования. Никлаус Вирт ( 1934 года рождения) — швейцарский учёный, специалист в области информатики, один из известнейших теоретиков в области разработки языков программирования, профессор информатики (компьютерных наук). Разработчик языка Паскаль и ряда других языков программирования.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Метод Гаусса
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции. Дана непрерывная функция f ( x ), которая содержит единственный корень на отрезке [ a,b ], где b > a при чем определены непрерывны и сохраняют знак f `( x ) f «( x ). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз. Метод Ньютона
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения. Заключение
Видео:Программа для решения корней квадратного уравнения с использованием дискриминанта на языке ПаскальСкачать
Предварительный просмотр:
Видео:Приложения для Учёбы | Полезно!Скачать

Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №7» г. Торжка
Программирование решения уравнений
Работа ученика 9Б класса
Смольков Андрей Владимирович
Ф.И.О. Борисова Ольга Александровна
Работа допущена к защите «_____» _______________ 2018г.
Подпись руководителя проекта _________________(__________________)
Видео:Python для самых маленьких. Линейные уравнения. Решение задачСкачать

Паспорт проекта
Название проекта
Программирование решения уравнений
Руководитель проекта
Борисова Ольга Александровна
Автор проекта
Смольков Андрей Владимирович
Учебная дисциплина
Информатика
Тип проекта
Исследовательский
Цель работы
Изучить программную среду PascalABC для решения уравнений
- Написать программу решения:
- Системы линейных алгебраических уравнений методом Гаусса
- Нелинейных алгебраических уравнений методом Ньютона
Результат проекта (продукт)
Программа в среде программирования PascalABC
Видео:Уроки C++ с нуля🔥Решение математических задач на языке С++🔥Переменные в языке С++🔥Скачать

Индивидуальный план работы над проектом
Выбор руководителя и темы проекта.
Выбор типа проекта. Составление плана работы над проектом.
Работа над проектом
Анализ теоретической части.
Составление плана защиты проекта.
Отзыв руководителя. Формирование папки индивидуального проекта.
Защита индивидуального итогового проекта
Видео:MIT App Inventor. Создание приложения для нахождения корней квадратного уравненияСкачать

Отзыв
на исследовательскую работу
учащегося 9 б класса МБОУ «Гимназия №7» г. Торжка
Смольков Андрей Владимирович
по теме: «Программирование решения уравнений»
Работа Смолькова Андрея представляет собой исследование программирование решения уравнений. Актуальность работы заключается в том, что на данный момент учащиеся 9-х классов изучают язык программирования Паскаль, и возникла необходимость объединить математику и информатику в единый программный продукт. В работе важно разобраться с различными методами решения уравнений и написать программу. Содержание работы соответствует заявленной теме. Работа включает в себя основную часть, заключение, список литературы. Работу Андрей выполнял самостоятельно, используя материалы Интернета и литературы. При выполнения работы Андрей проявил: самостоятельность, способность решать соответствующие проблемы. Не выполнял все рекомендации научного руководителя и не вовремя устранял замечания. Замечания по данной работе значительные, необходимо продумать и доработать заключение по данной теме. Не достаточно теоретического материала по языку программирования и их разновидности.
Вывод: проектная работа Смолькова А.В. по теме: «Программирование решения уравнений» достигла поставленных целей, отвечает требованиям, предъявляемым к индивидуальному итоговому проекту и рекомендуется к защите.
Учитель информатики . Борисова О.А.
(предмет) (подпись) (расшифровка подписи)
«__»_____________ 2018 г.
Видео:Решение уравнений, линейная программа на С++Скачать

Общие сведения о языке программирования Паскаль
Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами. Существует несколько тысяч языков программирования. Для данного проекта выбран язык программирования Паскаль, который был разработан в 70-х годах прошлого века Никлаусом Виртом (Швейцария). свое название этот язык получил в честь французского ученого Блеза Паскаля, известного не только своими достижениями в математике, физике и философии, но и созданием первой в мире механической машины, выполнявшей сложение двух чисел.
Язык Паскаль считается универсальным языком программирования, так как он может применяться для записи алгоритмов решения самых разных задач ( вычислительных, обработки текстов, построения графических изображений, поиска информации и т.д.). Он поддерживает процедурный стиль программирования, в соответствии с которым программа представляет собой последовательность операторов, задающих те или иные действия.
Основой языка программирования Паскаль, как и любого другого языка, является алфавит — набор допустимых символов, которые можно использовать для записи программы. Это:
- латинские прописные буквы;
- латинские строчные буквы;
- арабские цифры;
- специальные символы (знак подчеркивания, знаки препинания, круглые, квадратные и фигурные скобки, знаки арифметических операций и д.р.)
В языке существует также некоторое количество различных цепочек символов, рассматриваемых как единые смысловые элементы с фиксированным значением. Такие цепочки символов называются служебными словами.
В программе, записанной на языке Паскаль, можно выделить:
- заголовок программы;
- блок описания используемых данных;
- блок описания действий по преобразованию данных (программный блок).
Заголовок программы состоит из служебного слова program и имени программы. После имени программы ставятся точка с запятой. Блок описания данных состоит из раздела описания констант (const), раздела описания переменных (var) и некоторых других разделов. В разделе описания переменных указываются имена используемых в программе переменных и их типы. Имена переменных одного типа перечисляются через запятую, затем после двоеточия указывается их тип; описание каждого типа заканчивается точкой с запятой.
Общий вид программы:
Видео:НАХОДИМ КОРНИ КВАДРАТНОГО УРАВНЕНИЯ С ПОМОЩЬЮ PYTHON 🐍- If/Else **Программа решает за тебя!**Скачать

Решение системы алгебраических уравнений методом Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
В переменную n вводится порядок матрицы системы. С помощью вспомогательной процедуры Input вводятся двумерный массив A и одномерный массив b, после чего оба массива и переменная n передаются функции Gauss. В функции Gauss для каждого k-го шага вычислений выполняется поиск максимального элемента в k-м столбце матрицы начиная с k-й строки. Номер строки, содержащей максимальный элемент сохраняется в переменной l. В том случае если максимальный элемент находится не в k-й строке, строки с номерами k и l меняются местами. Если же все эти элементы равны нулю, то происходит прекращение выполнения функции Gauss c результатом false. После выбора строки выполняется преобразование матрицы по методу Гаусса.
Видео:Задача 411. Квадратное уравнение. acmp.ru C++Скачать

Решение нелинейных уравнений
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции.
Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f«(x). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз.
К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.
Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.
Видео:Решение квадратного уравнения на C# для Windows Forms в Visual Studio 2022Скачать

Заключение
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Язык программирования Паскаль является универсальным языком программирования. В нем можно выполнить самые различные решения уравнений. Язык достаточно прост и понятен для начинающих программистов.
Видео:Как решают уравнения в России и США!?Скачать

Список литературы
- Босова Л.Л. Информатика: учебник для 8 класса/ Л.Л. босова, А.Ю. Босова.-3-е изд.-М.: БИНОМ. Лаборатория знаний, 2015. — 160с.:ил.
- http://www.cyberforum.ru
- http://tpdn.ru/library/articles/52/13520
- http://pcfu.ru/metod-gaussa-dlya-resheniya-slau
Видео:Программа для решения математических задачСкачать

Текст публичного выступления
Здравствуйте уважаемые члены комиссии. Я Смольков Андрей, ученик 9Б класса МБОУ «Гимназии №7» города Торжка. Разрешите представить свой исследовательский проект по теме «Программирование решения уравнений». Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами. Существует несколько тысяч языков программирования. Для данного проекта выбран язык программирования Паскаль, который был разработан в 70-х годах прошлого века Никлаусом Виртом (Швейцария). Свое название этот язык получил в честь французского ученого Блеза Паскаля, известного не только своими достижениями в математике, физике и философии, но и созданием первой в мире механической машины, выполнявшей сложение двух чисел. Язык Паскаль считается универсальным языком программирования, так как он может применяться для записи алгоритмов решения самых разных задач ( вычислительных, обработки текстов, построения графических изображений, поиска информации и т.д.). Он поддерживает процедурный стиль программирования, в соответствии с которым программа представляет собой последовательность операторов, задающих те или иные действия. Основой языка программирования Паскаль, как и любого другого языка, является алфавит — набор допустимых символов, которые можно использовать для записи программы. Это: латинские прописные буквы; латинские строчные буквы; арабские цифры; специальные символы (знак подчеркивания, знаки препинания, круглые, квадратные и фигурные скобки, знаки арифметических операций и д.р.). В языке существует также некоторое количество различных цепочек символов, рассматриваемых как единые смысловые элементы с фиксированным значением. Такие цепочки символов называются служебными словами. В программе, записанной на языке Паскаль, можно выделить: заголовок программы; блок описания используемых данных; блок описания действий по преобразованию данных (программный блок). Заголовок программы состоит из служебного слова program и имени программы. После имени программы ставятся точка с запятой. Блок описания данных состоит из раздела описания констант (const), раздела описания переменных (var) и некоторых других разделов. В разделе описания переменных указываются имена используемых в программе переменных и их типы. Имена переменных одного типа перечисляются через запятую, затем после двоеточия указывается их тип; описание каждого типа заканчивается точкой с запятой. Общий вид программы:
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. На данных слайдах представлен программный продукт реализации решения уравнения методом Гаусса в Паскале. Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции. Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f«(x). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз. Программа на слайде. К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций. Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
🌟 Видео
Программа для решения квадратных уравнений на С++Скачать

Программа для решения уравненийСкачать