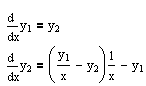Как создать дифференциальное уравнение в matlab (5 видео)

Содержание

Как создать дифференциальное уравнение в matlab
Решение ОДУ в Matlab
Обыкновенные дифференциальные уравнения
Методы решения дифференциальных уравнений
Метод Рунге-Кутта первого порядка
Метод Рунге-Кутта второго порядка
Метод Рунге-Кутта четвёртого порядка
Решение ОДУ в Matlab стандартными средствами
Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1
📺 Видео

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Как создать дифференциальное уравнение в matlab

Дифференциальные уравнения и системы уравнений

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).

Входными параметрами этих функций являются:

f — вектор-функция для вычисления правой части уравнения системы уравнений
interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
Х0 — вектор начальных условий системы дифференциальных систем
options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

массив Т — координаты узлов сетки, в которых ищется решение;
матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

В М-файле с именем pr 7. m пишем:

Потом в командном окне вызываем функцию ode113:

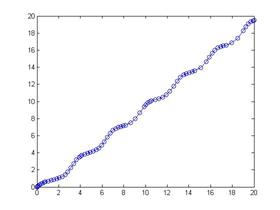
ode113(@pr7,[0 20],0) %Метод Адамса: @ pr 7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 — условие: y(0)=0

Результатом будет график:

Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:

В М-файле с именем pr 8. m пишем:

Потом в командном окне вызываем функцию ode 45:

Видео:MatLab. Решение дифференциального уравнения.Скачать

Решение ОДУ в Matlab

Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.

Обыкновенные дифференциальные уравнения

С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:

Задача Коши
Краевая задача
Задача на собственные значения

Кратко расскажу о их сути:

Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Методы решения дифференциальных уравнений

Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.

В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.

Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.

Метод Рунге-Кутта первого порядка

Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.

Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:

Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).

Погрешность Метода Рунге-Кутта 1 порядка

» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.

Метод Рунге-Кутта второго порядка

Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.

Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.

Метод Рунге-Кутта четвёртого порядка

Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.

Решение ОДУ в Matlab стандартными средствами

Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:

ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])

Входными параметрами этих функций являются:

f — вектор-функция для вычисления правой части уравнения системы уравнений;
interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
Х0 — вектор начальных условий системы дифференциальных уравнений;
options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

массив Т — координаты узлов сетки, в которых ищется решение;
матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.

Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:

На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».

Видео:Решение системы уравнений Колмогорова в МатлабеСкачать

Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

В среде MATLAB можно решать системы диффуров с начальными условиями, краевые задачи, а также решать дифференциальные уравнения в частных производных с помощью инструмента PDE toolbox.

В данном обзоре речь пойдет лишь о системах дифференциальных уравнений с начальными условиями, то есть о задаче Коши. В англоязычной литературе это называется Initial Value Problem.

каким образом записывать системы диффуров
как задать начальные условия
временной интервал
какой получать результат решения для дальнего использования

Решать системы обыкновенных дифференциальных уравнений можно как в MATLAB, так и в Simulink.

В первую очередь, следует определиться, использовать для решения Matlab и его текстовый редактор, или Simulink, где те же системы дифференциальных уравнений могут быть записаны в виде функциональных блоков.

Выбор ваш должен зависеть от задачи. Если Вы, например, хотите смоделировать какой-либо объект управления, описываемый системой диффуров, то в данном случае имеет смысл использовать именно Simulink, так как Вам, впоследствии, понадобиться синтез, например, системы управления, и Simulink подойдет здесь как нельзя лучше.

А вот если у Вас, например, есть необходимость решать системы диффуров с большим количеством уравнений и неизвестных, или специфика Вашей задачи требует особой и специальной настройки численного метода, а также если вы хотите использовать решение диффура в составе других скриптов MATLAB, то Вам имеет смысл решать дифференциальные уравнения способом, о котором пойдёт речь в этом обзоре.

Рассмотрим синтаксис решателей matlab.В качестве аргументов следует подать правую часть системы в виде MATLAB-функции.

На рисунке показан требуемый вид системы, когда выражены старшие производные.

Системы, чей вид отличается от требуемого, следует преобразовать к таковому.

Если функция простая, то её можно записать прямо в поле аргумента, однако, когда речь идёт о системах уравнений, имеет смысл записывать систему уравнений в виде отдельной функции, в том числе и в виде отдельного м-файла. Об этом мы поговорим чуть позже и на конкретном примере.

Также подается интервал времени, на котором будет найдено решение. Интервал задаётся строкой из двух чисел: начальной величины независимого аргумента t и его конечного значения.

Далее задаются начальные условия. Значения всех неизвестных искомых переменных в начале расчёта задаются в виде столбца соответствующей размерности.

Далее, при необходимости, задаются опции. Вот тут и раскрываются широкие возможности MATLAB по настройке решателя. Помимо управления точностью и величиной шага, имеется возможность обрабатывать данные в процессе вычисления, а также выполнять скрипты по завершению вычисления. Но ещё более полезным является опция отслеживания событий по условию, более подробно поговорим об этом дальше. Также есть другие специальные опции, которые могут быть использованы при решении определённых типов систем.

Вы могли заметить, что название функции — odeXY – это обозначение для всех решателей, которых всего 8 штук. В данном ролике мы пользоваться решателем ode45, соответствующего численному по методу Дормана-Принса 4(5). Этого решателя достаточно для подавляющего большинства задач. Остальные решатели будут подробно рассмотрены в приложении к задачам соответствующих типов позже.

Перейдем к примерам.

Рассмотрим 2 примера:

решение дифференциального уравнения первого порядка.
решение системы двух дифференциальных уравнений второго порядка.

В качестве уравнение первого порядка рассмотрим логистическое уравнение Ферхюльста, которое описывает динамику численности популяции. Суть уравнения такова: скорость прироста населения y пропорциональна количеству населения, однако лимитирована максимальной численностью популяции.

Забавный факт: Ферхюльст назвал это уравнение логистическим, и никто до сих пор не знает почему, ибо сам Ферхюльст об этом никому не рассказал.

Решение этого дифференциального уравнения выглядит следующим образом.

Пишем функцию в явном виде, задаём интервал расчёта и записываем начальное условие. Пару слов о записи функции подобным образом. Знак собаки в матлабе является оператором создания функции соответствующих переменных. Вы задаёте аргументы функции и саму функцию через пробел, как показано на рисунке.

Перейдем в окно MATLABа и посмотрим, как это выглядит.

Так выглядит скрипт:

Так выглядит график решения дифференциального уравнения:

В качестве примера решения системы, состоящей из двух дифференциальных уравнений второго порядка, рассмотрим шарик, подвешенный на пружине, который ещё и тормозит о воздух.

Уравнения показаны на рисунке. Но вид системы отличается от требуемого, в том числе потому, что в нём присутствуют вторые производные. Для приведения системы в требуемый вид выполним 2 простых шага:

Первое: следует заменить переменные соответствующим образом. Теперь у нас 4 неизвестных. Далее следует преобразовать уравнение с учетом замены. Таким образом, мы имеем систему из четырёх дифференциальных уравнений первого порядка.

Настало время её записать.

Итак, мы имеем систему, параметры, интервал времени и начальные условия. Решим же эту задачу скорее.

В отличие от предыдущего примера, систему четырех уравнений проблематично записать в поле аргумента. Поэтому всю систему будем записывать в отдельную функцию.

Эту функцию можно располагать как в самом скрипте решения в самом его конце, так и в виде отдельного m-файла.

На выходе функция должна представлять собой вектор-столбец, который записывается перечислением компонент через точку запятой как показано на рисунке.

Теперь рассмотрим скрипт самого решения.

На этот раз запишем интервал и начальные условия в виде переменных MATLAB. Интервал, соответственно, в виде строки, а начальные условия – в виде столбца длинной 4.

Сообразно с уже разобранным ранее синтаксисом укажем функцию pendulum_np, интервал времени и начальные условия.

Перейдем теперь в окно MATLAB и посмотрим решение.

Так выглядит скрипт:

Запускаем скрипт и получаем графики:

Зачастую хочется, чтобы одну и ту же систему можно было бы решать с разными параметрами, и при этом не менять их в теле самой функции. И это можно, и даже нужно осуществлять.

На рисунке показана функция MATLAB, которая соответствует движению подвешенного на пружине шара, однако можно заметить, что эта функция теперь имеет на 5 аргументов больше.

Параметры задаются в скрипте, а при вызове функции мы обращаемся к уже известному оператору-собаке, которая превращает функцию семи переменных pendulum_n в функцию двух переменных t и X. Вот и всё.

Я вам очень рекомендую разобраться с тем, как работает оператор-собака. В хелпе он называется function-handle. Разобравшись с ним Вам будет работать в среде MATLAB ещё проще и ещё приятнее.

Вывод: не так страшно решать диффуры

Под конец стоит сказать какие вообще системы дифференциальных уравнений матлаб может решать, а может он решать системы практически любых типов.

Их можно, с одной стороны, разделить по степени жёсткости, а с другой стороны, по структуре самой системы.

Когда уравнения представляют поведение системы, которая содержит ряд быстрых и медленных реакций, то такую систему уравнения можно назвать жесткой. Для жестких задач явные численные методы работают плохо, или не работают вовсе. Примером жесткой задачи может являться протекание тока через клеточную мембрану. На самом деле, чёткого разделения между жесткими и нежёсткими системами не существует. Степень жесткости системы формально определяется через собственные значения матрицы Якоби, но давайте не будем закапываться.

Видеообзор по теме решения систем Д/У доступен по ссылке.