Как создать блок схему для уравнения

Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.

В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.

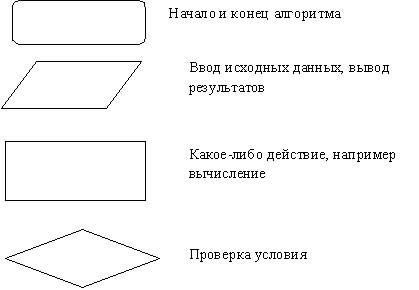
Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).

Существует несколько основных видов блоков, которые нетрудно запомнить:

Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.

Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».

Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.

Составим алгоритм решения подобных задач:

1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.

Запишем условие в более кратком виде.

Решение задачи №1

Структура программы, решающей данную задачу, тоже проста:

• 1) Описание переменных;
• 2) Ввод значений сторон прямоугольника;
• 3) Расчет площади прямоугольника;
• 4) Расчет периметра прямоугольника;
• 5) Вывод значений площади и периметра;
• 6) Конец.

А вот и решение:

Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.

Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:

Дано: V1, V2, S, Т
Найти: S1

Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).

Формула, используемая для решения нашей задачи, выглядит следующим образом:

Следующий пункт алгоритма – блок-схема:

Решение задачи №2.

А также решение, записанное в Pascal :

Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число! А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:

Обратите внимание в Паскале, как и в любом другом языке программирования десятичная дробь вводится с точкой, а не с запятой!

Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real. Вот, как выглядит исправленная программа:

Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

Здесь понятней чем в школе.

мля… прикиньте, я узнал про этот сайт только ПОСЛЕ того как сделал программу с условием, узнавая все в инструкции

Ребята , вопрос на засыпку, как заставить «,» (введенную пользователем в числе) заменить на «.» внутри программы, что бы не вылетало юхни с ошибкой.

Взять строку введенную пользователем, заменить «,» на «.».
Если совсем гуглить не умеете, то вам сюда — http://www.cyberforum.ru/pascal/thread190664.html

>> скорость машины не обязательно круглое число!

Нет такого понятия, как «круглое число».

Обе ваши блок-схемы не соответствуют ГОСТу (сдать такие на курсовой проект не получится). ГОСТ определяет блоки начала и конца, как «прямоугольник со скругленными краями», а не «скругленными углами».

>> умение правильно и быстро составлять схемы является фундаментом, основой программирования.

Большинство программистов так не считает. Кроме того, попробуйте поспрашивать у программистов «когда они последний раз составляли блок-схему?» — окажется что в ВУЗе (когда с них зачем-то сдирали знание ГОСТа).

>> так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

Очень сложное, долгое и бесполезное занятие. Для хоть сколько-нибудь большой программы (в тысячу строк хотя бы, как курсак) блок-схемы будут огромные и их будут десятки. А что делать если они перестают соответствовать коду? — вот даже в вашей первой задаче надо будет добавить проверку, что юзер не ввел отрицательные значения сторон, что делать? — исправления кода займут 1 минуту, а исправление блок-схем 10 минут, и зачем тогда этим заниматься?

Программист не должен писать блок-схемы (он их должен читать и понимать и при необходимости исправлять). Блок-схемы это графический язык общения, который понимает как программист, так и не программист. Чтобы пользователь не общался с программистом своими «хотелками», типа я хочу, чтобы вот это правильно считалось, и это число складывалось с этим, а потом выводилось сюда (или вообще говорил — хочу что бы работало), а рисовал все в виде блок-схем с четким алгоритмом. Тогда по идее у программиста будет понимание того, что от него хотят (и он через пять минут не забудет все что ему сказали). Либо, когда общаются два программиста пишущих на разных языках программирования (LISP и Java) и одному нужно объяснить как работает его код, что бы другой переписал его на другом языке.
Как объяснить преподавателю как работает программа, если преподаватель не знает языка программирования на котором написана ваша программа? Или как преподавателю объяснить алгоритм задачи студентам пишущим и реализующим этот алгоритм или программу на разных языках программирования? Нужен какой-то универсальный язык общения и обычно это просто текст «что нужно сделать» на русском языке, а не намного облегчающая жизнь программиста блок-схема.
Вам могут сказать — сделай модуль авторизации (ты же знаешь как, ну как всегда и как везде), а могут нарисовать блок-схему модуля авторизации с учетом всех пожеланий, типа того, что пароль должен содержать не менее 6 символов и что нужно делать в противном случае т.д. То есть блок схему должен уметь рисовать тот кто ставит задачу, а не программист. Либо программист (архитектор либо менеджер проекта), который ставит задачу другим программистам.

Вы слишком придирчивы, серьезно (я говорю про последние два пункта). Понятно, что статья (как почти и весь сайт) написана почти только для школьников, которым об этом твердят в школе. Здесь же им просто объясняют те вещи, которые они на учебе недопоняли

Блок схемы всей программы могут не понадобиться. Это же тонны бумаги и много времени. И да, они устаревают и актуализировать их трудоёмко.
Но при обсуждении новых вариантов решения задачи с другими программистами удобно оперировать блоками с криво-косо нарисованными краями и линиями. Начертил на бумаге или доске и все понятно.
На практике я встречал фотографии доски с блок-схемами, прикреплённые к задачам в Jira.
Не по ГОСТу 🙂

Спасибо, теперь я напишу программу, которая делает код по блок схеме и наоборот

program Logarifm;
Var
X,y,z:real;
function Lgrfm(A,B:Real):Real;
var
Osn:Real;
begin
Osn:=ln(A)/ln(B);
Lgrfm:=Osn;
end;
begin
Write(‘Введите X = ‘);
ReadLn(X);
Write(‘Введите Y = ‘);
ReadLn(Y);
Z:=Lgrfm(X,2)+Lgrfm(Y,3);
WriteLn(‘Z = ‘,Z:10:3);
ReadLn;
end.

Отличный сайт, мне все нравится все понятно и четко, нашел нужные программы.

В блок-схемах начало и конец алгоритма обозначаются не прямоугольником со скруглёнными краями, а овалом!

Ребята, что сделали сайт молодцы)) Оч полезная инфа, что нужно поправить, чтобы сайт стал еще лучше:
1) мне не хватает структуры уроков порядковой (или хотябы под уроками чтобы была ссылка на следующий), поэтому приходится на другие уроки искать ссылки по сайту и в контексте уроков;
2)нет описания функций используемых в примерах (по крайней мере, возможно по причине отсутствия структуры, я их не нашел), поэтому беру на сторонних ресурсах описания таких функций как dec() inc() sqr() odd().
А вообще как я понял сайт составлялся школьниками «на коленках», поэтому я не придираюсь, а просто говорю им спасибо за их труд. Желаю успехов.

Видео:Создания блок-схемы при помощи кодаСкачать

Основные блок-схемы решения линейных и квадратичных задач с параметрами

Разделы: Математика

Задачи с параметрами (ЗсП) традиционно являются наиболее сложными для учащихся, поскольку требуют от них умения логически рассуждать и проводить анализ решения. Подобные задачи являются первыми исследовательскими задачами, с которыми встречаются школьники. Для их решения не требуются знания, выходящие за пределы школьной программы, но недостаточно применения лишь стандартных приемов, а необходимо глубокое понимание всех разделов элементарной математики.

В данной статье предпринята попытка систематизации и формализации (в форме блок-схем) наиболее часто встречающихся и наиболее типичных ЗсП. При этом выделены классы задач, решаемых по единой методике.

Рассматриваются аналитические методы решения ЗсП, сводящиеся к исследованию линейных или квадратных уравнений (неравенств), а также квадратного трехчлена. Такой выбор обусловлен тем, что курс школьной математики ограничен «вглубь», по существу, «теорией квадратичного».

Линейные уравнения

Определение. Уравнение вида ax=b, где a, b принадлежат множеству всех действительных чисел, будем называть стандартным видом линейного уравнения. Всевозможные варианты, возникающие при решении линейных уравнений, отразим в блок–схеме I.

Количество корней линейного уравнения отразим в блок-схеме II:

Пример 1. Для всех действительных значений параметра m решите уравнение m 2 x–2=4x+m.

Решение. Приведем заданное линейное уравнение к стандартному виду:

m 2 x–2=4x+m, m 2 x–4x=m+2, (m 2 –4)x=m+2.(1)

Следуя схеме I, рассмотрим два случая для коэффициента при x:

1)если m 2 – 4 не равно 0, m не равно ±2, то x=(m+2)/(m 2 -4), x=1/(m–2);

а) при m = –2 уравнение (1) примет вид 0х=0, отсюда х – любое действительное число;

б) при m = 2 уравнение (1) примет вид 0х= 4, отсюда следует, что корней нет.

Ответ. Если m 2 то x=1/(m–2); если m= – 2, то x – любое действительное число; если m=2, то корней нет.

Пример 2. При каких значениях параметра k уравнение 2(k–2x)=kx+3 не имеет корней?

Решение. 2(k–2x)=kx+3, (k+4)x=2k–3. В силу схемы II уравнение не имеет корней, если k+4=0 и 2k–3 не равно 0 => k= –4 и k не равно 1,5 => k = –4.

Ответ. k=–4.

Системы линейных уравнений

Определение 1. Система называется совместной, если она имеет хотя бы одно решение.

Определение 2. Система называется несовместной, если она не имеет ни одного решения.

Количество решений системы линейных уравнений отразим в блок-схеме III.

Замечание. Так как уравнение прямой y=kx+b в общем виде записывается следующим образом ax+by+c=0, то взаимное расположение двух прямых отразим в блок-схеме IV.

Пример. При каких значениях параметра c система из двух уравнений c 2 x+(2–c)y–4=c3 и (2c–1)y+cx+2=c 5 совместна?

Решение. Запишем систему в стандартном виде: c 2 x+(2–c)y=c 3 +4 и cx+(2c–1)y=c 5 –2. Сначала найдем значения c, при которых эта система не имеет решений. В силу схемы III имеем условие,

c 2 /с=(2-с)/(2с–1), с не равно (c 3 +4)/(c 5 –2),

которое равносильно системе из уравнения и неравенства

с=(2–с)/(2с–1) и с не равно (c 3 +4)/(c 5 –2).

Решением системы является с=1. Итак, система имеет решения при всех действительных значениях с, кроме с=1.

Ответ. с — любое действительное число, с не равно 1.

Линейные неравенства

Определение. Неравенство вида ax>b, ax b, ax b, отразим в блок-схеме V.

Пример. Для всех значений параметра m решите неравенство 5x–m>mx–3.

Решение. 5x–m>mx–3, (5–m)x>m–3.

Следуя схеме V, рассмотрим три случая для коэффициента при х:

2)если 5–m 5, то x 2. Откуда следует, что решений нет.

Ответ. Если m (m–3)/(5–m); если m=5, то решений нет; если m>5, то х 2 +bx+c=0, где a, b, c — любые действительные числа, a>0, называется квадратным уравнением относительно действительного переменного x.

Ситуации, возникающие при решении квадратных уравнений, отразим в блок–схеме VI.

Пример. При каких значениях параметра c уравнение (c–2)x 2 +2(с–2)x+2=0 не имеет корней?

Решение. Рассмотрим два случая:

1) если с–2 не равно 0, c не равно 2, то D 2 –2(c–2) 2 +(c+4)x+c+7=0 имеет только отрицательные корни?

Решение. В силу условия задачи необходимо рассмотреть два случая (линейный и квадратичный):

1) если c–1=0, c=1, то уравнение примет вид 5x+8=0, x= –5/8 – отрицательный корень;

2) если c–1 не равно 0, c не равно 1, то, следуя схеме VII, получим систему

Решением ее являются промежутки –22/3 2 +bx+c, где a не равно 0, называется квадратичной. График квадратичной функции называется параболой.

Абсциссы точек пересечения параболы y=ax 2 +bx+c с осью (Ox) являются корнями уравнения ax 2 +bx+c=0.

Учитывая это, отразим взаимное расположение параболы и оси (Ox) в следующей схеме:

Замечание. Если уравнение параболы имеет вид y=a(x–p) 2 +q, то (p; q) – координаты вершины параболы.

Пример 1. При каких значениях параметра a вершина параболы y=(x–7a) 2 +a 2 –10+3a лежит в III координатной четверти?

Решение. Пусть (x₀, y₀) – координаты вершины параболы. В силу замечания имеем x₀=7a, y₀=a 2 –10+3a. Так как вершина параболы лежит в третьей четверти, то

Ответ. –5

Пример 2. При каких значениях параметра b график функции y=(4–b 2 )x 2 +2(b+2)x–1 лежит ниже оси (Ox)?

Решение. Рассмотрим два случая.

1. Пусть 4–b 2 =0, b= + 2;

1) если b=2, то прямая y=8x–1 не лежит ниже оси (Ox);

2) если b= –2, то прямая y= –1 лежит ниже оси (Ox).

2. Пусть 4–b 2 не равно 0. Тогда в соответствии со схемой VIII получим

Объединяя ответы, получим b 2 +bx+c=0. Введем функцию y(x)= ax 2 +bx+c. Тогда расположение корней этого уравнения на числовой оси отразим в блок–схеме IX.

Следствие. С учетом схемы IX схема VII для знаков корней квадратного уравнения примет следующий вид:

Пример. При каких значениях параметра a корни уравнения x 2 –2(a+3)x+a 2 +6,25a+8=0 больше 2?

Решение. Введем функцию y(x)=x 2 –2(a+3)x+a 2 +6,25a+8; x₀ – абсцисса вершины этой параболы. Так как корни уравнения находятся справа от числа 2, то в соответствии со схемой IX имеем:

Решение. Данная задача равносильна следующей: при каких значениях параметра b система

имеет одно решение?

Решим неравенство (2): 2x 2 –2x–1>0, x_1,2=0,5(1±(3) 1/2 ), x 1/2 ) или x>0,5(1+(3) 1/2 ).

Найдем корни уравнения (1): D=(2b–7) 2 , x₁=2, x₂=2b–5. Поскольку корень x₁=2 удовлетворяет неравенству (2), то система имеет одно решение в следующих случаях:

1) если x₂=2b–5 не удовлетворяет неравенству (2), то 0,5(1–(3) 1/2 ) 1/2 ) или 0,25(11–O3) 1/2 );

Ответ. 0,25(11–(3) 1/2 ) 1/2 ), b=3,5.

Пример 2. При каких значениях параметра p уравнение 5–4sin 2 x–8cos 2 (x/2)=3p имеет корни?

Решение. Преобразуем заданное уравнение:

5– 4sin 2 x–8cos 2 (x/2)=3p => 5–4(1–cos2x)–4(1+cosx)=3p => 4cos 2 x–4cosx–3p–3=0.

Сделаем замену cosx=t. Тогда заданная задача равносильна следующей: при каких значениях p система

4t2–4t–3p–3=0, (1)
-1 2 –4t–3p–3; t₀–вершина этой параболы. В силу схемы IX случаи 1, 2 и 3 описываются следующей совокупностью:

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Как создать блок схему для уравнения

Данный материал представляет собой справочное руководство по составлении алгоритмов, которые являются необходимой составной частью контрольной и курсовой работы по дисциплине «Информатика».

Изложенный материал не претендует на полноту охвата всех сторон проблемы алгоритмизации при решении задач, возникающих на практике. Однако его вполне достаточно для того, чтобы разобраться и выполнить ту часть названных работ, которая необходима для составления алгоритмов и их описания.

Опыт показывает, что трудности, возникающие при составлении алгоритмов имеют как общий характер, когда студент не может уяснить принцип работы алгоритма вообще, так и частный, когда непонятным оказывается отдельный фрагмент алгоритма.

В любом случае рекомендуется обратить внимание на следующее. Разбирая или составляя алгоритм, нужно мысленно представить некоторый автомат по обработке данных (компьютер), который будет выполнять действия, предписанные этим алгоритмом. Без такого представления невозможно понять сам алгоритм. Ниже, при разборе примеров, станет понятно, что такой мысленный автомат совсем несложен. Во всяком случае он несравнимо проще реального компьютера, хотя общие принципы их функционирования в основном одинаковы. Допустимо (например, при составлении описания) отождествлять работу такого автомата с работой самого алгоритма.

При изучении материала особенно первоначальном, следует подробно разобраться в каждом алгоритме, начиная с самого первого и самого простого. Начинать нужно с полного уяснения пяти самых простых и самых необходимых понятий: константа, переменная, ячейка памяти, запись константы в ячейку памяти, чтение константы из ячейки памяти . Не пренебрегайте этими советами, так как очень скоро убедитесь, что при разборе следующего алгоритма обязательно натолкнетесь не только на те же трудности, но присовокупите к ним новые. Более того, нередко полное понимание даже самого простого алгоритма дает намного больше пользы, чем поверхностное изучение десятка алгоритмов повышенной сложности.

Видео:0.Блок схема. 8 классСкачать

1. Алгоритм и алгоритмизация

Алгоритм – это инструкция о том, в какой последовательности нужно выполнить действия при переработке исходного материала в требуемый результат. [ последователь­ность точных предписаний, понятных исполните­ лю (компьютеру, роботу и пр.), совершить последо­ вательность действий, направленных на достиже­ ние конкретного результата. ]

Наряду с понятием алгоритма используют термин алгоритмизация , под которой понимают совокупность приемов и способов составления алгоритмов для решения алгоритмических задач.

Часто алгоритм используется не как инструкция для автомата, а как схема алгоритмического решения задачи. Это позволяет оценить эффективность предлагаемого способа решения, его результативность, исправить возможные ошибки, сравнить его еще до применения на компьютере с другими алгоритмами решения этой же задачи. Наконец, алгоритм является основой для составления программы, которую пишет программист на каком-либо языке программирования с тем, чтобы реализовать процесс обработки данных на компьютере.

Неотъемлемым свойством алгоритма является его результативность , то есть алгоритмическая инструкция лишь тогда может быть названа алгоритмом, когда при любом сочетании исходных данных она гарантирует, что через конечное число шагов будет обязательно получен результат.

На практике получили известность два способа изображения алгоритмов:

в виде пошагового словесного описания;

в виде блок-схем.

Первый из этих способов получил значительно меньшее распространение из-за его многословности и отсутствия наглядности. Второй, напротив, оказался очень удобным средством изображения алгоритмов и получил широкое распространение в научной и учебной литературе. Именно этот способ будет использован ниже при составлении и описании алгоритмов.

Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

2. Блок-схема и ее элементы

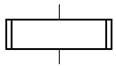
Блок-схема – это последовательность блоков, предписывающих выполнение определенных операций, и связей между этими блоками. Внутри блоков указывается информация об операциях, подлежащих выполнению. Конфигурация и размеры блоков, а также порядок графического оформления блок-схем регламентированы ГОСТ 19002-80 и ГОСТ 19003-80 «Схемы алгоритмов и программ».

В табл. 1 приведены наиболее часто используемые блоки, изображены элементы связей между ними и дано краткое пояснение к ним. Блоки и элементы связей называют элементами блок-схем.

Представленных в таблице элементов вполне достаточно для изображения алгоритмов, которые необходимы при выполнении студенческих работ.

При соединении блоков следует использовать только вертикальные и горизонтальные линии потоков.

Горизонтальные потоки, имеющие направление справа налево, и вертикальные потоки, имеющие направление снизу вверх, должны быть обязательно помечены стрелками.

Прочие потоки могут быть помечены или оставлены непомеченными.

Линии потоков должны быть параллельны линиям внешней рамки или границам листа

Название

Элемент

Комментарий

Вычислительное действие или последовательность вычислительных действий

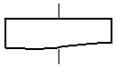
Обращение к процедуре

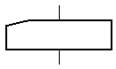
Вывод данных, печать данных

Разрыв линии потока

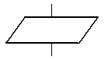
Начало, конец, пуск, останов, вход и выход во вспомогательных алгоритмах

Используется для размещения надписей

Горизонтальные и вертикальные потоки

Линии связей между блоками, направление потоков

Слияние линий потоков

Расстояние между параллельными линиями потоков должно быть не менее 3 мм , между остальными элементами схемы – не менее 5 мм .

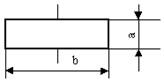
Горизонтальный и вертикальный размеры блока должны быть кратны 5 мм (делиться на 5 нацело). Отношение горизонтального и вертикального размеров блока b/а = 1.5 является основным. При ручном выполнении блока допустимо отношение b/а = 2.

Блоки «Начало», «Конец» и «Соединитель» имеют высоту а/2, т. е. вдвое меньше основной высоты блоков.

Для размещения блоков рекомендуется поле листа разбивать на горизонтальные и вертикальные (для разветвлявшихся схем) зоны.

Для удобства описания блок-схемы каждый ее блок следует пронумеровать. Удобно использовать сквозную нумерации блоков. Номер блока располагают в разрыве в левой верхней части рамки блока.

По характеру связей между блоками различают алгоритмы линейной, разветвляющейся и циклической структуры.

Примеры, пояснявшие изложенное, можно найти в блок-схемах алгоритмов, которые будут приведены ниже.

Видео:Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

3. Константы, переменные и ячейки памяти

Для того чтобы ясно представить как «работает» алгоритм, опишем простейший автомат, который предназначен для выполнения операций, предписанных этим алгоритмом.

В состав такого автомата входят:

память, состоящая из отдельных ячеек;

процессор, т. е. устройство, способное выполнять операции, в том числе математические, и отдавать головке указания читать данные из ячеек или записывать данные в ячейки памяти автомата.

Головка, получив указание от процессора, может записывать в ячейку или считывать из нее одну константу .

В простейшем случае константой является любое арифметическое число. Например, 12, 0.78, 0, –45.33 и т. д. ( Константами могут быть такие строки символов, структуры данных и др.).

Под простой переменной , или просто переменной будем понимать некоторую ячейку памяти, т. е. отдельное место для хранение одной константы. В отдельной ячейке за время работы алгоритма может побивать множество различных констант (отсюда название – переменная). Такими ячейками (электронными, магнитными, оптическими) снабжен реальный компьютер.

Переменные имеют буквенно-символьное обозначение. Например, 1, n, a, a1, b , H2 – переменные. Одновременно обозначение переменной является индексом ячейки, в которую будут записываться константы. Любая из таких констант называется значением переменной . Например, Z является переменной и адресом ячейки Z одновременно. С алгоритмической точки зрения понятия “переменная” и “адрес ячейки” памяти являются идентичными.

Запись вида Y = 5.5 следует понимать так: записать константу 5.5 в ячейку с адресом Y (если до этой операции в ячейку была записана константа, то она будет затерта, а на ее место будет помещена константа 5.5). Произносить эту запись следует так: “переменной Y присвоить значение 5.5” .

Запись вида L = M следует понимать так: прочитать константу, расположенную по адресу M и скопировать эту константу в ячейку с адресом L (при этом константа из ячейки M не удаляется, а остается такой, какой она была до чтения). Произносить эту запись нужно так: «переменной L присвоить значение переменной M (или просто: L присвоить M)».

Видео:как ... нарисовать блок-схему в WORD, EXCEL, POWER POINT, VISIOСкачать

4. Массивы

Другой разновидностью переменных являются так называемые индексированные переменные или массивы . Массив – это некоторая совокупность ячеек, объединенная одним обозначением (массивом может быть одна ячейка). Всякий массив обязательно имеет размерность. Массивы бывают одномерными, двумерными, трехмерными и т. д.

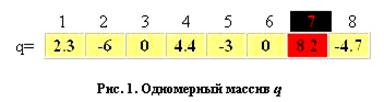
Одномерный массив – это последовательность ячеек, расположенных в одну линию. На рис. 1 приведен пример такого массива.

Массив имеет имя q. Для того чтобы можно было отличить одну ячейку массива от другой ячейки этого же массива, их нумеруют. Нумерация ячеек обычно начинается с 1. Номер ячейки массива называется его индексом , а константа в ячейке – элементом массива. Теперь становится возможной работа с отдельной ячейкой такого массива. Например, команда q 7 = 8.2 означает, что в 7-ю ячейку массива q надлежит записать константу 8.2. Команда r 41 = q 2 + q 5 означает, что нужно сложить константы, записанные во 2-ю и 5-ю ячейки массива q, и результат записать в 41-ю ячейку одномерного массива r. Эту же операцию можно описать другими словами: 41-му элементу массива r присвоить значение суммы 2-го и 5-го элементов массива q.

Двумерный массив по расположению ячеек напоминает математическую матрицу ( рис. 2 ). Элемент такого массива характеризуется двумя индексами: первый показывает строку, в которой расположена ячейка, второй – ее столбец. Например, команда d 2, 5 = 43 означает, что в ячейку, размещенную на пересечении 2-й строки и 5-го столбца двумерного массива d, нужно записать константу 43.

Аналогично устроена структура массивов трех- и большей размерности.

Видео:#7 Как автоматически построить блок схему из JavaScript кодаСкачать

5. Линейные алгоритмы

Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца.

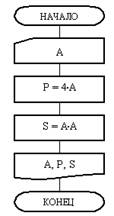
На рис. 3 приведен пример блок-схемы алгоритма вычисления периметра Р и площади S квадрата со стороной длины A.

Рис. 3. Линейный алгоритм

Блок-схема алгоритма состоит из шести блоков. Выполнение алгоритма начинается с блока 1 «Начало». Этот блок символизирует включение автомата, настройку его на выполнение алгоритма и выделение памяти под все переменные, которые задействованы в алгоритме. В алгоритме рис. 3 таких переменных три: A, Р, S. Следовательно, под каждую из них алгоритмом будет выделено по одной ячейке памяти. На этом блок 1 будет отработан.

Как видно из рис.3, блок 1 связан вертикальной линией потока с блоком 2. Эта линия не имеет стрелки, указывавшей направление потока. Следовательно, этот поток направлен вниз. Таким образом, после выполнения блока 1 управление будет передано на блок 2. Блок 2 «Перфокарта» ( см. табл. 1) показывает, что переменной A следует присвоить значение. Это означает, что в ячейку, отведенную автоматом под эту переменную, нужно поместить константу. На реальной компьютере эта константа может быть введена самыми разными способами. Способ зависит от того, как запрограммирован данный фрагмент. Можно, например, потребовать ввод константы с клавиатура или получить его из заранее подготовленного файла. Возможно эта константа будет получена через внешние источники данных, например, от физической установки, подключенной к компьютеру.

Для данного примера способ передачи константы не имеет значения, важно лишь то, что при выполнении блока 2 в ячейку с адресом А будет занесена конкретная константа. Пусть такой константой является число 5.

Далее управление по линии потока передается к блоку 3 «Процесс». В этом блоке при выполнении размещенной в ней команды число 4 умножается на константу, помещенную в ячейку А (т. е. 5), и результат (т. е. 20) присваивается переменной Р (т. е. константа 20 записывается в ячейку по адресу Р). После выполнения этих операций управление передается к блоку 4.

В блоке 4 аналогичным образом производится умножение значений переменной А и результат (константа 25) присваивается переменной S (в ячейку по адресу S будет занесена константа 25). После этого выполняется переход к блоку 5.

При выполнении команд блока 5 выводятся (например, на экран, бумагу, во внешний файл и т. д.) значения переменных А, Р, S, которые сохранились в соответствующих ячейках к этому моменту. Понятно, что для конкретного примера А = 5 будут выведена константы 5, 20, 25, т. е. длина сторона квадрата, его периметр и площадь. Далее управление передается последнему блоку 6.

В блоке б “Конец” производится освобождение ячеек памяти, которые были зарезервированы под переменные А, P, S, и алгоритм заканчивает работу.

Понятно, что при новом запуске этого же алгоритма можно получить совсем другие числа. Так, если в блоке 2 переменной А присвоить значение 20, то алгоритм выдаст в блоке 5 константы 20, 80, 400.

Детальное описание алгоритма рис. 3 приведено для того, чтобы показать, в какой последовательности автомат выполняет предписанные операции и как при этом меняется состояние памяти автомата, т. е. для того, чтобы объяснить суть происходящих в автомате процессов. Из сказанного нужно уяснить, что автомат выполняет предписанную ему работу шаг за шагом. Всякий шаг обрабатывается процессором. Помимо вычислений процессор при необходимости отдает команды считывавшей/записывавшей головке, что и куда записывать, откуда читать. Конечный результат следует искать в ячейках памяти, каждая из которых до окончания алгоритма имеет известный адрес и хранит записанную в нее константу.

При выполнении контрольной или курсовой работы нет нужды давать столь подробное описание алгоритма. Тем не менее, описание должно быть выполнено с той степенью полноты, которая позволяет дать ясное представление о всех сторонах и особенностях алгоритмического процесса.

Видео:Блок схема.Работа в ворде. WordСкачать

6. Разветвляющиеся алгоритмы

На практике алгоритмы линейной структуры встречается крайне редко. Чаще необходимо организовать процесс, который в зависимости от каких-либо условий проходит по той либо иной ветви алгоритма. Такой алгоритм называется разветвляющимся.

В блок-схемах ветвление начинается на выходах элемента «Решение», с помощью которого в алгоритме выполняется проверка какого-либо условия. Количество ветвей тем больше, чем больше проверяемых условий.

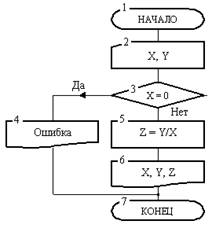
Для пояснения рассмотрим решение задачи нахождения значения функции z = y/x.

На первый взгляд представляется, что алгоритм решения этой задачи имеет линейную структуру. Однако, если учесть, что делить на нуль нельзя из-за переполнения ячейки, то, во-первых, нужно из вычислений исключить вариант х = 0 и, во-вторых, проинформировать пользователя алгоритма о возникшей ошибке. Если этого не сделать, то при вычислениях может возникнуть аварийный выход до получения результата. В профессиональной практике аварийные завершения крайне нежелательны. т. к. к этому моменту уже может быть накоплено определенное количество результатов, которые окажутся необработанными и попросту пропадут. Можно привести другие примеры, когда аварийный останов компьютера может повлечь куда более серьезные последствия.

Решение задачи представлено блок-схемой рис. 4.

Рис. 4. Разветвляющийся алгоритм

Она состоит из 7 блоков. После начала работы алгоритм в блоке 2 требует ввода аргументов X и Y. Затем в блоке 3 производится проверка условия X = 0. Здесь автомат проверяет равна ли нули константа, введенная в ячейку с адресом X. Результатом такой проверки является ответ «Да» или «Нет». В зависимости от этого ответа выполнение алгоритма пойдет по одной или другой ветви. Если результат проверки окажется отрицательным, то на х можно делить и управление передается блоку 4.

В блоке 4 будет получен результат Z, затем в блоке б значения всех трех переменных будут отпечатаны и в блоке 7 алгоритм закончит работу. Если же ответ окажется положительным, то управление будет передано блоку 4. Выполняя команду блока 4, автомат выведет сообщение «Ошибка» и затем закончит работу в том же блоке 7.

Видео:Построение логических схемСкачать

7. Циклические алгоритмы

Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами . Алгоритмы, содержащие циклы, называется циклическими . Использование циклов существенно сокращает объем алгоритма.

Различают циклы с наперед известным и наперед неизвестным количеством проходов.

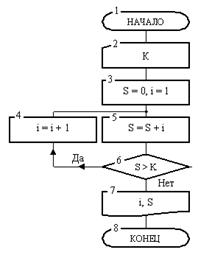
Пример 1. Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, . сумма которых больше числа К.

Рис. 5. Разветвляющийся алгоритм

Блок-схема алгоритма решения этой задачи приведена на рис. 5. Она состоит из восьми блоков.

После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5.

В нем при выполнении команды S = S + i производится сложение содержимого ячеек S и i, а результат записывается в ячейку S. Поскольку до операции сложения было S = 0, i = 1, то после операции будет S = 1. При записи нового значения старое содержимое ячейки S (нуль) стирается, а на его место записывается число 1.

Нужно обратить внимание на то, что если бы до этой операции в блоке 3 не была выполнена команда S = 0 (записать нуль в ячейку S ), то при нахождении суммы S + 1 возникла бы ошибка, поскольку из ячейки S была бы извлечена константа, которая оказалась там после распределения памяти.

После суммирования первого члена последовательности в блоке 6 выполняется проверка условия о превышении суммы S заданного числа К.

Если условие 6 не выполнится, то производится переход к блоку 4, где при выполнении операции значение переменной увеличивается на 1 и становится равным 2. Теперь алгоритм вновь вернется к блоку 5 и к старому значении суммы добавит новый член 2. После этого сумма станет равной 3. В блоке б вновь проверяется условие получения требуемой суммы и т. д. Цепочка блоков 5-4 будет обрабатываться вновь и вновь до того момента, когда однажды при определенном значении переменной i, наконец, выполнится условие S > К, т. е. когда накапливаемая в таком цикле сумма впервые превысит заданное значение К. Переменная i, значение которой при очередном проходе цепочки этих блоков увеличивается на 1, играет роль счетчика этого цикла.

Далее производится переход к блоку 7, где отпечатается значение количества членов ряда (извлечено и отпечатано число из ячейки i, которое там хранится в момент выполнения условия), суммы S и в блоке 8 алгоритм закончит работу.

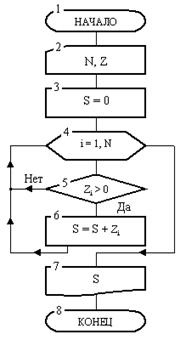
Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N ( под длиной массива понимается количество его элементов ). Блок-схема алгоритма дана на рис. 6.

Рис. 6. Циклический алгоритм

Вначале в блоке 2 производится ввод двух переменных N и Z. Первая из них представляет одну ячейку. В нее записывается одна константа – число, равное количеству элементов массива Z. Именно такое количество ячеек объединяет другая переменная – Z.

Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда самое N еще не известно (оно будет введено позже Z). Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к дальнейшему накоплению необходимой суммы.

Блоки 4-6 представляет собой сам цикл, в котором накапливается сумма.

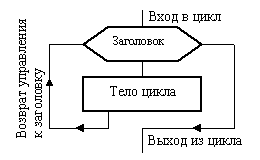
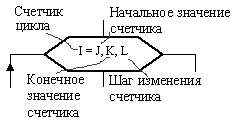
Для того чтобы понять, как функционирует не только этот, а и любой другой цикл, обратимся к рис. 7, 8. На них показана общая структура цикла и его важнейшие параметры.

Как видно из рис. 7, цикл состоит из заголовка и тела. Всякий цикл обязательно имеет свой счетчик.

На рис. 8, где показана структура и параметры заголовка цикла, роль такого счетчика выполняет переменная i. Внутри заголовка после счетчика и символа «=» через запятую указывает начальное и конечное значения счетчика и шаг его изменения (на рис. 8 их роль выполняют переменные j, k, l соответственно). Если значение шага l = l, то его можно не указывать.

Сначала производится вход в цикл. После этого начинается его выполнение.

Рис. 7. Структура цикла Рис. 8. Структура заголовка цикла

Внутри заголовка счетчику первоначально присваивается значение i = j. Затем выполняется блоки, образующие тело цикла. Обработка блоков внутри цикла производится по часовой стрелке. В результате после первого выполнения тела цикла управление вновь передается заголовку. Здесь к текущему значению счетчика добавится шаг. Теперь, если новое значение счетчика не вышло за свои пределы (т. е. не стало больше своего конечного значения при положительном шаге или меньше конечного значения – при отрицательном шаге), то снова выполняется тело цикла, вновь после возврата к заголовку к счетчику добавляется шаг. Так цикл будет выполняться до тех пор, пока значение счетчика однажды не выйдет за предписанный предел. Как только такой предел будет преодолен, произойдет выход из цикла и управление будет передано блоку, который следует сразу за циклом.

Вернемся к блок-схеме рис. 6. Заголовок ее цикла представлен блоком 4. Роль счетчика цикла играет переменная i, которая должна в цикле изменяться от 1 до N. Поскольку шаг явно не указан, то по умолчанию он подразумевается равным 1. Тело цикла образуют блоки 5 и 6.

Сразу после входа в цикл переменная i примет начальное значение i = 1. Далее в блоке 5 выполняется проверка положительности первого элемента массива Z (т. к. i = 1). Если этот элемент действительно положителен, то в блоке б он будет добавлен к переменной S, после чего выполняется возврат к заголовку цикла. Если этот элемент не положителен (т. е. нуль или отрицательный), то будет выполнен переход сразу к заголовку цикла, минуя блок суммирования 6.

На втором круге цикла счетчик i в заголовке увеличится на 1 и станет равным 2. Теперь, при новом выполнении тела цикла, в блоке 5 проверяется на положительность второй элемент массива Z и, если он положителен, то добавляется в сумму и т. д. Последний раз тело цикла выполнится при i = N. При этом значении счетчика проверяется последний элемент массива. Наконец, в заголовке цикла i примет значение N+1. Это значение выходит за предписанный предел, следовательно, произойдет выход из цикла и управление перейдет блоку 7. В этом блоке выводится накопленная сумма и алгоритм закончит работу.

Видео:Алгоритмы и структуры данных простыми словами. Зачем учить алгоритмы? #codonaftСкачать

8. Алгоритмы со структурами вложенных циклов

Нередко при алгоритмическом решении задачи возникает необходимость создания цикла, содержащего в своем теле другой цикл. Такие вложенные друг в друга циклы относятся к структурам вложенных циклов . Порядок вложенности циклов, когда в теле внутреннего цикла содержатся другие циклы, может быть достаточно большим. Этот порядок определяется методом, с помощью которого достигается решение поставленной задачи. Так, при обработке одномерных массивов, как правило, удается построить алгоритмическую схему без вложения циклов. Однако в ряде случаев при решении таких задач без вложенных циклов не обойтись.

Рис. 9. Алгоритм сортировки массива

Отметим, что все вложенные друг в друга циклы, включая наружный, должны иметь счетчики с различными именами. Вне этих циклов счетчики могут быть использованы как обычные переменные или как счетчики других циклов.

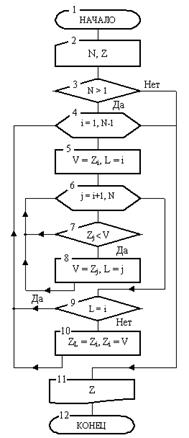
Пример 1. Рассмотрим задачу сортировки одномерного массива Z длины N. Отсортировать массив – значит расположить его элементы в порядке роста или убывания.

Опишем метод сортировки массива в порядке роста. Сначала выполняется проход по массиву с целью определения в нем наименьшего элемента. Затем производится перестановка этого элемента с первым. Далее совершается второй проход по массиву, начиная со второго элемента. Найденный наименьший элемент переставляется со вторым и т. д. После (N-1)-го прохода с выполнением названных операций массив окажется отсортированным.

Блок-схема этого алгоритма сортировки показана на рис. 9. Она включает 12 блоков. После начала работы в блоке 2 переменная N и массив Z заполняются константами. Затем в блоке 3 проверяется условие о том, нужно ли сортировать массив.

Это сводится к установлению факта наличия в массиве нескольких элементов, т. к. массив из одного элемента всегда отсортирован. Если этот факт установлен, то алгоритм приступает к сортировке. Процедура сортировки выполняется в цикле, объединяющем блоки 4-10. В теле этого цикла содержится другой цикл, который образован блоками 6-8. Его назначение станет ясно из дальнейшего разбора алгоритма.

После входа в наружный цикл его счетчик i примет значение 1, что в рамках нашего метода подразумевает первый проход по массиву.

Далее будут выполнены блоки 5-10, составляющие тело наружного цикла. В блоке 5 размещены две вспомогательные переменные V и L. Первая из них предназначена для фиксирования наименьшего элемента, а вторая – для запоминания его индекса. Так как i = 1, то при первом проходе в блоке 5 V примет значение первого элемента, а L значение 1. Затем во внутреннем цикле, образованном блоками 6-8, где его счетчик j будет изменяться от 2 до N, последовательно проводится сравнение соответствующих элементов массива Z со значением переменной V. При этом всякий раз, как будет найден меньший чем v элемент, значение V будет заменено на значение этого элемента, а в переменной L будет зафиксирован его индекс. Понятно, что после выполнения внутреннего цикла в переменной V будет содержаться значение, равное наименьшему элементу, а в L – индекс этого элемента. В блоке 9 далее проверяется, не является ли наименьший элемент первым элементом массива. Если это не так, то в блоке 10 на место наименьшего элемента (его номер L) запишется первый (т. к. при первом проходе L =1 ), а на место первого элемента – наименьший (он равен V). После этого произойдет возврат управления к заголовку наружного цикла блоку 4. В нем значение счетчика станет равным i = 2.

Затем вновь выполняется его тело, но уже для нового значения счетчика i. Теперь с помощью блоков 5-10 отыскивается наименьший элемент массива начиная с номера 2. Затем в блоках 9-10 он займет второе место в массиве и т. д. Когда тело наружного цикла выполнится (N-1), раз массив будет отсортирован.

В блоке 12 отсортированный массив будет выведен и в блоке 13 алгоритм окончит работу.

Алгоритмы со структурами вложенных циклов часто используют при решении задач обработки двумерных массивов. В таких алгоритмах счетчики циклов используются для манипуляции с индексами массивов.

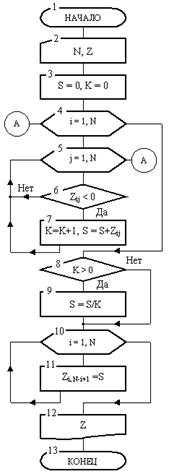
Пример 2. Дан двумерный квадратный массив Z, состоящий из N строк и N столбцов. Необходимо найти среднее арифметическое S его отрицательных элементов и заменить положительные элементы побочной диагонали массива средним арифметическим S.

Рис. 10. Блок-схема алгоритма

Блок-схема алгоритма показана на рис. 10. Она состоит из 13 блоков. В блоке 2 переменная N и весь массив Z заполняются константами. В блоке 3 рабочие переменные S и К получает значение нуль. Переменная S сначала будет играть роль сумматора отрицательных элементов массива, затем после накопления суммы она примет значение среднего арифметического. Переменная К нужна для подсчета количества отрицательных элементов массива.

В блоках 4-7 выполняется накопление суммы отрицательных элементов массива.

Эти блоки образует два вложенных цикла, причем внутренний цикл со счетчиком j является телом наружного цикла со счетчиком i. Проанализируем работу этой структуры.

После входа в наружный цикл в блоке 4 переменная i примет значение i = 1. Далее будет выполнено его тело ( блоки 5-7 ), которое, в свою очередь, также является циклом. После входа во внутренний цикл в блоке 5 переменная j примет значение j = 1. Затем в блоке 6 проверяется на отрицательность элемент массива Z, расположенный в первой строке и первом столбце, т. к. i = 1 и j = 1.

Если он окажется отрицательным, то в блоке 7 переменная К увеличится на 1, а к S добавляется значение этого элемента. После этого выполняется возврат к блоку 5, т. е. к заголовку внутреннего цикла. Здесь j увеличится на 1, станет равной j = 2 и управление перейдет к блоку 6. В нем проверяется элемент, стоящий все в той же первой строке, но во втором столбце (i = 1, j = 2). Если он окажется отрицательным, то К снова увеличится на 1, а к накопленному к этому времени S добавляется значение этого элемента и т.д. Когда полностью выполнится внутренний цикл, т. е. переменная j «пробежит» от 1 до N, в переменную S накопится сумма всех отрицательных элементов первой строки массива, а в К – их количество. Теперь управление передается к блоку 4 заголовка наружного цикла, где i станет равной i = 2. Снова будет отработано его тело, т. е. цикл 5-7. При этом будет найдена уже сумма отрицательных элементов первых двух строк массива, а в К сохранится количество этих элементов. Когда выполнится весь наружный цикл, в S будет константа, равная сумме отрицательных элементов всего массива, а в К – их количество. Теперь управление перейдет к блоку 8. Если окажется, что в массиве есть отрицательные элементы (К>0), то в блоке 9 вычисляется среднее арифметическое как отношение суммы элементов к их количеству. Результат помещается а ту же переменную S. Отметим, что если бы блок 8 проверки отсутствовал, то при К = 0 (в массиве нет ни одного отрицательного элемента) в блоке 9 из-за деления на нуль возникла бы ошибка. Эта ошибка повлекла бы аварийное завершение вычислений до окончания работы алгоритма.

Далее выполняется блоки 10-11, которые также образует цикл. В нем производится замена элементов побочной диагонали на среднее арифметическое S (побочной диагональю является прямолинейная цепочка ячеек в диапазоне от нижнего левого угла до верхнего правого угла массива). Обратите внимание, на то что переменная i, которая использовалась ранее, в целях экономии памяти применяется вновь.

Проследим работу этого цикла. После входа в блок 10 счетчик примет значение i = 1. Затем в блоке 11 при этом значении будет вычислен индекс столбца элемента N – 1 + i = N. Таким образом, элемент с индексами (1, N) станет равным S. На втором круге цикла i увеличится на 1 и станет i = 2. Нетрудно видеть, что теперь элемент (2, N-1) станет равным S и т. д. На последнем круге цикла элемент (N, 1) получит значение S, что завершит изменение значений всех элементов побочной диагонали на среднее арифметическое S.

Наконец, в блоке 12 измененный массив будет выведен и в блоке 13 алгоритм закончит работу.

Видео:Урок 4. Формулы Excel для начинающихСкачать

9. Вспомогательные алгоритмы

Вспомогательный алгоритм является аналогом языковой подпрограммы. Он имеет имя и может иметь параметры, которые называются формальными параметрами . Имя служит для того. чтобы отличить его от других алгоритмов, а формальные параметры, которые напоминают переменные математических функций, выполняют роль входных и выходных параметров.

Формальные параметры должны быть выбраны таким образом, чтобы ими был исчерпан весь набор необходимых входных и выходных величин. Нередко один и тот же параметр может оказаться входным и выходным одновременно. Например, на вход такого алгоритма может быть подан массив для обработки, а на выходе процедуры он может предстать в измененном виде как выходной параметр.

Среди вспомогательных алгоритмов различают процедуры и функции .

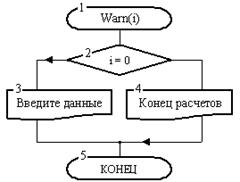
Рис. 11. Процедура Warn

Первый блок схемы рис. 11 в отличие от ранее рассмотренных примеров, где этот блок имел наименование “Начало”, включает имя процедуры Warn и один формальный параметр i. С помощью этого имени в алгоритме рис. 12 выполняется обращение именно к этой процедуре.

Из схемы видно, что если на вход процедуры Warn подать i = 0, то она в блоке 3 выдаст сообщение «Введите данные». При любом другом i будет выведено сообщение «Конец расчетов». Этим исчерпываются возможности процедура Warn.

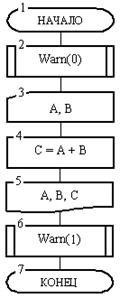
На рис. 12 дана схема головного алгоритма ( первый блок имеет наименование «Начало» ). Этот алгоритм в блоках 2 и 8 обращается к процедуре Warn.

Опишем последовательность и механизм обработки данных, которые предписаны алгоритмами рис. 11 и 12.

Рис. 12. Головной алгоритм

Выполнение алгоритмических действий всегда начинаются с головного алгоритма. Поэтому сначала будет выполнен блок 1 схемы рис. 12. Далее в блоке 2 головной алгоритм выполняет обращение к процедуре Warn при конкретном значении ее аргумента (0). Это конкретное значение называется фактическим параметром процедуры.

Теперь управление временно переходит в алгоритм рис. 11 процедуры Warn. Здесь и далее по всей процедуре Warn формальный параметр i заменяется на фактический параметр 0 (нуль) всюду, где он встречается.

Далее обрабатывается блок 2 процедуры, где с учетом сказанного проверяется условие 0 = 0. Результатом проверки станет перевод управления к блоку 3, в котором выводится сообщение «Введите данные». На этом процедура заканчивается и управление вновь передается в головной алгоритм к блоку 3.

Далее в блоках 3-5 алгоритма рис. 12 выполняются уже понятные действия по вводу, суммированию и выводу переменных. Затем управление передается в блок б, который содержит новое обращение к процедуре Warn с фактическим параметром 1.

Снова управление переключается на схему рис. 11, где вместо формального параметра i всюду записывается фактический параметр – константа 1. Поскольку в блоке 2 условие 1 = 0 не выполнится, то будет выполнен блок 4 и алгоритм выведет сообщение «Конец расчетов». После этого управление возвращается в головной алгоритм к блоку 7, где и будет окончательно завершен алгоритмический процесс.

Внешне такой процесс может выглядеть примерно так. На экран выводится сообщение «Введите данные» и компьютер переходит в режим ожидания ввода двух констант с клавиатуры. Затем после их ввода на экране появляется три константы и надпись «Конец работы». На первый взгляд может показаться, что процедуры лишь усложняют решение задачи. Действительно, рассмотренную здесь задачу проще решить одним алгоритмом, не прибегая к составление процедуры. Однако при составлении алгоритма решения сложной задачи очень быстро становится ясно, что без использования процедур обойтись просто невозможно. На практике при решением серьезных алгоритмических задач часто одному программисту не под силу выполнить весь объем работ. Поэтому над ее решением работает обычно коллектив программистов под руководством координатора. Образно говоря, координатор здесь работает как головной алгоритм, а его программисты как процедуры. При этом каждый программист (часто независимо от других) получает от координатора задание по составление процедур определенного назначения. В результате такой организации работы задача получает разрешение.

Видео:3 Метод простой итерации Блок-схема Решение системы линейных уравнений СЛАУСкачать

10. Декомпозиция алгоритма

Под декомпозицией алгоритма понимают разложение его o6щeй алгоритмической схемы на вспомогательные алгоритмы (процедуры и функции) и головной алгоритм. Напомним, такая задача ставится перед студентом при выполнении курсовой или контрольной работы. Одним из условий, которое должно быть обязательно выполнено, является наличие в работе хотя бы одной процедуры или функции (кроме того, работа должна содержать текст описания всех процедур и головного алгоритма).

Метод, при помощи которого обычно выполняется декомпозиция, достаточно прост. Сначала вычленяют основные этапы предстоящей работы. Наиболее сложные этапы оформляет в процедуры или функции верхнего уровня. Затем, если необходимо, такие этапы делят на этапы более низкого уровня. Наиболее сложные из них также оформляют процедурами или функциями и т. д. Следуя методу «от сложного к простому», в конечном итоге достигают решения поставленной задачи. Приведем пример декомпозиции для решения задачи сортировки массива. Эта задача была решена ранее в разд. 8 (рис. 9) без использования вспомогательных алгоритмов. Решение задачи декомпозиции состоит из трех основных этапов: 1) ввода данных, 2) сортировки массива и 3) вывода отсортированного массива. Первый и третий этапы вследствие их простоты не нуждаются в дальнейшей декомпозиции, поэтому выполняются в головном алгоритме. Второй этап представляет достаточно сложный и самостоятельный фрагмент вычислений, поэтому его целесообразно выделить в отдельную процедуру, которой можно дать имя Sort.

Этап сортировки, в свои очередь, состоит из двух этапов: 1) установления необходимости сортировки и (N–1) – кратного прохода по массиву и 2) нахождения наименьшего элемента во фрагменте массива и перестановки этого элемента с начальным элементом фрагмента. Поскольку последний этап многократно повторяется при выполнении первого этапа, то его можно оформить в отдельную процедуру. Этой процедуре можно дать имя Tra (от английского transposition – перестановка). Блок-схемы головного алгоритма, процедуры Sort и процедуры Тrа показаны на рис. 13-15 соответственно.

Рис. 13. Головной алгоритм Рис. 14. Процедура Sort

Дадим краткое, описание взаимодействия этих алгоритмов в ходе решения задачи сортировки.

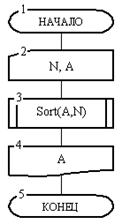
Рис. 15. Процедура Tra

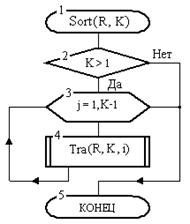
Выполнение начинается с головного алгоритма (рис. 13). В блоке 2 вводятся исходные данные, затем в блоке 3 выполняется сортировка массива. В блоке 4 отсортированный массив выводится и алгоритм заканчивает работу. Сортировка массива в блоке 3 головного алгоритма выполняется обращением к процедуре Sort, показанной на рис. 14. Переменные A и N являются фактическими параметрами, Переменные А и N, которые использованы в блок-схеме алгоритма Sort, является формальными параметрами.

При обращении к процедуре Sort на вход подаются параметры A и N. В результате в теле процедуры производится замена формального параметра R на фактический параметр A, аналогично формальный K заменяется на фактический N.

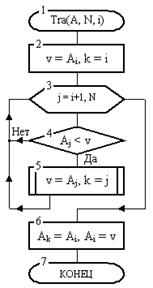
Далее в блоке 2 проверяется необходимость сортировки массива R. Затем, если такая необходимость будет установлена, в цикле 3-4 будет выполняется сортировка массива. При всяком значении счетчика цикла в его теле производится нахождение наименьшего элемента фрагмента и его перестановка с начальным элементом этого фрагмента. Эти операции выполняются отдельно с помощью процедуры Tra. Как видно из рис. 15, на вход процедуры Tra нужно подать имя массива (A), количество элементов (N) и номер элемента (i), которым начинается фрагмент. В теле процедуры в блоках 2-5 отыскивается наименьший элемент фрагмента (v) и его номер (k). Затем в блоке 6 выполняется вышеназванная перестановка элементов.

Таким образом, весь процесс управляется головным алгоритмом, который выполняет сортировку посредством обращения к вспомогательному алгоритму – процедуре Sort.

Тот, реализуя решение своей задачи, в своя очередь несколько раз вымывает еще более простой вспомогательный алгоритм процедуру Tra. В результате такого взаимодействия достигается решение задачи в целом.

В заключение приведем пример алгоритма-функции . Она похожа на процедуру, но в отличие от последней должна в теле алгоритма еще содержать команду присваивания результата имени функции , т. к. результат после вычислений сохранится в переменной, представленной именем функции.

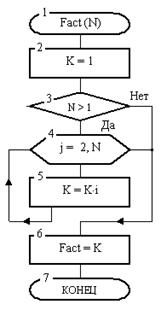
Рассмотрим задачу вычисления факториала числа N! = 1 . 2 . 3 . . . N. Результатом будет одно число, поэтому лучше алгоритм оформить в виде функции.

Рис. 16. Функция Fact

Ее блок-схема показана на рис. 16. Переменная К используется для накопления произведения и, поскольку 0! = 1 и1! = 1, то в блоке 2 ей сразу присваивается значение 1. Далее, если N>1, то в цикле, образованном блоками 4-5, накапливается искомое произведение и помещается в переменную К. В блоке 6 имя Fact функции получает значение вычисленного произведения из ячейки К. Для процедур действия, размещенного в блоке 6, не может быть, а для функций оно должно быть обязательно, поскольку иначе значение функции на выходе окажется неопределенным.

Обращение к функции в других алгоритмах (головных, процедурах, функциях) производится по ее имени.

При этом оно может входить в состав выражений. В качестве фактических параметров могут быть использованы как переменные, константы, так и целые выражения. Важно только, чтобы фактический параметр был совместим по типу с формальным, который содержится в заголовке описания алгоритма.

Пример использования функции Fact показан на рис. 17. В операторе присваивания используется обращение к функции для N = 6. После передачи этого значения в алгоритм рис. 16 и вычислений внутри него результат будет сначала присвоен имени функции, т. е. переменной Fact, а затем в операторе присваивания — переменной L.

💡 Видео

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Математика это не ИсламСкачать

«Открытое интервью» с российским футурологом Сергеем ПереслегинымСкачать

Блок-схема циклического алгоритма. Вычисление n!Скачать

Как быстро нарисовать блок-схемы бизнес-процессов для технического задания CRMСкачать

Урок по работе с VisioСкачать

Основы программирования / Урок #6 – Блок схемы и алгоритмы действийСкачать

Как строить блок-схемы и рисовать бизнес-процессы [для начинающих]Скачать