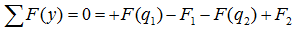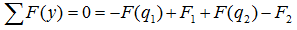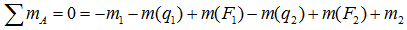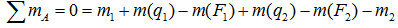Правила знаков для моментов и проекций сил на оси координат:
- Правило знаков проекций сил
- Правило знаков для моментов
- Как определить реакции в опорах?
- Что такое реакция опоры?
- Что вы должны уже уметь?
- Должны уметь находить сумму проекций сил
- Должны уметь составлять сумму моментов относительно точки
- Должны разбираться в основных видах опор
- Примеры определения сил реакций опор
- Определение реакций опор для балки
- Определение реакций опор для балки с распределенной нагрузкой
- Определение опорных реакций для плоской рамы
- Момент силы и правило моментов
- теория по физике 🧲 статика
- Виды равновесия
- Устойчивое равновесие
- Неустойчивое равновесие
- Безразличное равновесие
- Момент силы
- Правило моментов
- Условия равновесия тел
- Простые механизмы
- Наклонная плоскость
- Рычаг
- Неподвижный блок
- Подвижный блок
- 📸 Видео
Видео:Определение реакций опор простой рамыСкачать

Правило знаков проекций сил
То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.
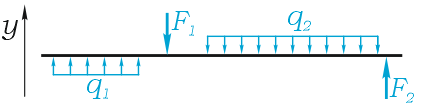
Например, для такой схемы нагружения:
уравнение суммы сил имеет вид
А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:
Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.
Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

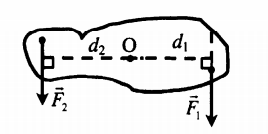
Правило знаков для моментов
Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

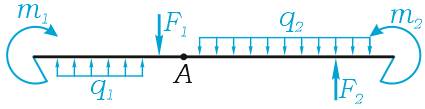
Например, для суммы моментов относительно точки A
или, что одно и то же
Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.
При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Определение реакций опор в балке. Сопромат.Скачать

Как определить реакции в опорах?
Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Видео:Момент силы относительно точки и осиСкачать

Что такое реакция опоры?
Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.
В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!
Что вы должны уже уметь?
В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.
Должны уметь находить сумму проекций сил
Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!
Должны уметь составлять сумму моментов относительно точки
Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:
На изображении показано, как определить момент силы F, относительно точки O.
Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:
- Если сила относительно точки крутит ПРОТИВ часовой стрелке, то момент положительный.
- Если она крутит ПО часовой стрелки, то соответственно момент отрицательный.
Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.
Должны разбираться в основных видах опор
Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.
Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как Ri, где i — точка крепления опоры.
Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.
Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.
Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Примеры определения сил реакций опор
Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.
Определение реакций опор для балки
Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:
Для этой расчетной схемы, выгодно записать такое условие равновесия: 
Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как RA и RB:
Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила RB поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB.
Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:
После нахождения реакций, делаем проверку:
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:
Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:
Определение опорных реакций для плоской рамы
Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:
Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим глобальную систему координат x и y.
Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:

Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию HA:
И, наконец, третье уравнение, позволит найти реакцию RA:
Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.
Расчет же показал, что RA, направленна в другую сторону:
В итоге, получили следующие реакции в опорах рамы:
Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:
Как видим, расчет реакций выполнен правильно!
На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!
Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂
Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.
Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

Момент силы и правило моментов
теория по физике 🧲 статика
Статика — раздел механики, изучающий условия равновесия тел.
Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Виды равновесия
Устойчивое равновесие
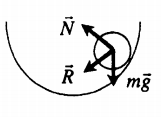
Неустойчивое равновесие
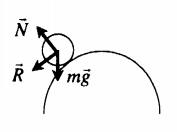
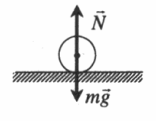
Безразличное равновесие
Видео:Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

Момент силы
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
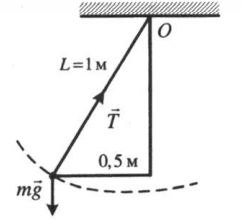
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
Момент силы может быть положительным и отрицательным.
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
Видео:Как научиться составлять уравненияСкачать

Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑ M п о ч а с . с т р . = ∑ M п р . ч а с . с т р .
Видео:Урок 76. Задачи на правило моментовСкачать

Условия равновесия тел
| Тело не участвует в поступательном движении: | |
| Тело не участвует во вращательном движении: | |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) | |
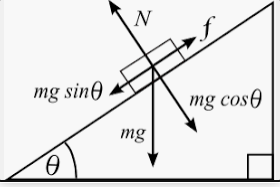 | Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: Рычаг |
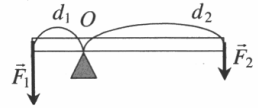 | Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F 1 F 2 . . = d 2 d 1 . . Неподвижный блок |
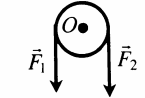 | Изменяет направление действия силы. Модули и плечи сил при этом равны: Подвижный блок |
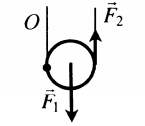 | Дает выигрыш в силе в 2 раза: |
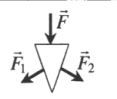 | Делит силу на две равные части, направление которых зависит от формы клина: |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Алгоритм решения
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
Запишем правило моментов:
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
Отсюда масса рыбы равна:
m 2 = m 1 d 1 d 2 . . = 0 , 8 · 0 , 3 0 , 4 . . = 0 , 6 ( к г )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Сформулировать определение плеча силы.
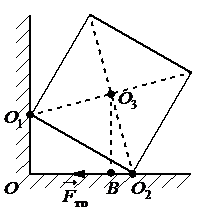
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
pазбирался: Алиса Никитина | обсудить разбор | оценить
📸 Видео
Составление уравнений реакций горения. 11 класс.Скачать

Ионные уравнения реакций. Как составлять полные и сокращенные уравненияСкачать

Момент силыСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Момент силыСкачать

Математика это не ИсламСкачать

Химические уравнения. СЕКРЕТНЫЙ СПОСОБ: Как составлять химические уравнения? Химия 8 классСкачать

ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ ХИМИЯ 8 класс // Подготовка к ЕГЭ по Химии - INTENSIVСкачать