Как составлять уравнение касательной к графику функции у f x в точке х0 (2 видео)

Содержание

Уравнение касательной к графику функции
п.1. Уравнение касательной
п.2. Алгоритм построения касательной
п.3. Вертикальная касательная
п.4. Примеры
Как составить уравнение касательной к графику функции
Как составлять уравнение касательной в заданной точке
Алгоритм написания уравнения
Задачи на написание уравнения касательной
Видео
Уравнение касательной и уравнение нормали к графику функции
Как получить уравнение касательной и уравнение нормали
Решаем задачи вместе
Решить задачи самостоятельно, а затем посмотреть решения
Снова решаем задачи вместе
Видео

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Уравнение касательной к графику функции

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_x+underbrace_ $$

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Как составлять уравнение касательной к графику функции у f x в точке х0

Пусть (f(x)=x^2+3).
Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).

Пусть (f(x)=sqrt[5]+1).
Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]+1=1)
(f'(x)=frac15(x-1)^+0=frac15(x-1)^=frac<5(x-1)^> )
(f'(x_0)=frac<5(1-1)^>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0).
Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4)
По условию (f'(x_0)=tgalpha=tg45^circ=1)
Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac=x-frac98 end

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2).
Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0).
Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac=-frac) begin f'(x)=left(fracright)’-x’=frac-1=frac=\ =frac=- frac end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac=-fracRightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac+14=frac+14=-18+14=-4\ y=-frac(x+14)-4=-frac end Уравнение касательной при (x_0=8) begin f(x_0)=frac-8=frac-8=-2\ y=-frac(x-8)-2=-frac end
Ответ: точка касания (-14;-4), уравнение (y=-frac)
и точка касания (8;-2), уравнение (-frac)

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac-frac+6=frac=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt> end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми:
(y=2x) и (y=2x-1).
Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt=0,2sqrt=frac<sqrt>)
Ответ: (frac<sqrt>)

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Как составить уравнение касательной к графику функции

Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Как составлять уравнение касательной в заданной точке

При написании уравнения будем использовать следующие обозначения:

x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
f(x) — исходная функция;
f'(x) — производная от функции;
k — угловой коэффициент.

Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.

Алгоритм написания уравнения

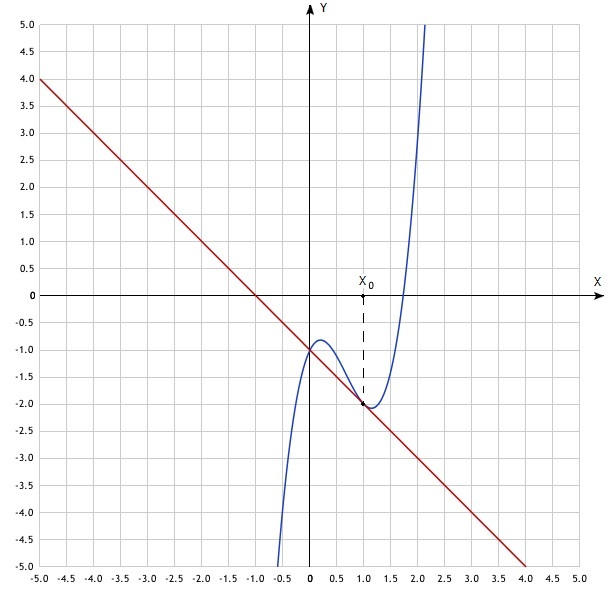
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:

Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.

В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.

Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.

Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.

Видео:ЕГЭ 2017 Профильный №7 найти производную в точке касания #7Скачать

Задачи на написание уравнения касательной

Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.

Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.

Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.

Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
Возьмем от функции производную: f'(x) = 4x.
Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.

В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.

Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).

Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
Запишем производную: g'(x) = 6x².
Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.

Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.

Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.

Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Видео

Закрепить это тему вам поможет видео.

Видео:Уравнение касательнойСкачать

Уравнение касательной и уравнение нормали к графику функции

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Как получить уравнение касательной и уравнение нормали

Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:

Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Видео:Уравнение касательной к графику функции | Алгебра 10 класс #45 | ИнфоурокСкачать

Решаем задачи вместе

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Видео:Как составить уравнение касательной и нормали к графику функцииСкачать

Решить задачи самостоятельно, а затем посмотреть решения

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Снова решаем задачи вместе

Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):