Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
- А теперь к задачам!
- Уравнение движения тела. Все виды уравнений движения
- Материальная точка
- Основные понятия
- Равномерное движение по прямой
- Относительность движения
- Пример составления уравнений
- Если скорость отрицательна
- Движение с увеличением скорости
- Если ускорение отрицательно
- Сложное движение
- Механическое движение
- Механическое движение
- Прямолинейное равномерное движение
- Скалярные величины (определяются только значением)
- Векторные величины (определяются значением и направлением)
- Проецирование векторов
- Уравнение движения
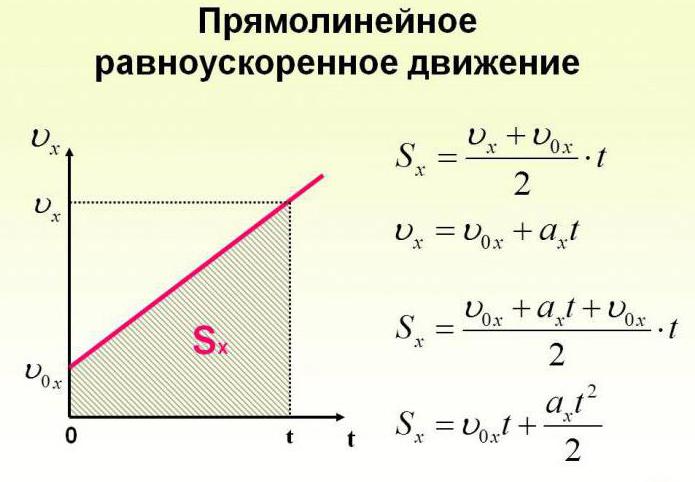
- Прямолинейное равноускоренное движение
- Уравнение движения и формула конечной скорости
- Движение по вертикали
- 🎥 Видео
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Задача на составление описания движения и составление уравнения движения по заданному графику движения
Дано: график движения тела
Найти:
1. составить описание движения
2. составить уравнение движения тела.
Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c
Составляем уравнение движения тела:
Записываем формулу уравнения прямолинейного равномерного движения.
Подставляем в нее найденный коэффициент Vx (не забываем о минусе!).
Начальная координата тела (Xо) соответствует началу графика, тогда Xо=3
Составляем описание движения тела:
Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!
Тело движется прямолинейно и равномерно из начальной точки Xо=3м со скоростью 0,75 м/с противоположно направлению оси X.
Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)
Движение тел задано уравнениями движения для каждого тела.
Дано:
1. уравнение движения первого тела
2. уравнение движения второго тела
Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел
По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.
Точка пересечения двух графиков движения определяет:
1. на оси t — время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X — координату места встречи (относительно начала координат)
В результате:
Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.
Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:
Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:
График движения — это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t1 и t2.
Для этих значений t подсчитываем соответствующие значения координат X1 и X2.
Откладываем 2 точки с координатами (t1, X1) и (t2, X2) и соединяем их прямой — график готов!
Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения
Задача 1
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.
Задача 2
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 3
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 4
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя — это частный случай движения, когда скорость тела равна нулю).
Задача 5
Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с
Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения
Видео:Физика - уравнения равноускоренного движенияСкачать

Уравнение движения тела. Все виды уравнений движения
Понятие «движение» определить не так уж просто, как это может показаться. С житейской точки зрения, это состояние является полной противоположностью покоя, но современная физика считает, что это не совсем так. В философии под движением подразумеваются любые изменения, происходящие с материей. Аристотель полагал, что данное явление равносильно самой жизни. А для математика любое перемещение тела выражается уравнением движения, записанным при помощи переменных и цифр.
Видео:Используя график скорости, составить уравнение движения тела, имеющего начальную координату -10 м.Скачать

Материальная точка
В физике перемещение различных тел в пространстве изучает раздел механики, именуемый кинематикой. Если размеры некоего объекта слишком малы в сравнении с расстоянием, которое ему приходится преодолевать вследствие его движения, то он рассматривается здесь как материальная точка. Примером тому может служить автомобиль, едущий по дороге из одного города в другой, птица, летящая в небе, а также многое другое. Подобная упрощенная модель удобна при написании уравнения движения точки, за которую принимается определённое тело.
Бывают и другие ситуации. Представим, что тот же автомобиль хозяин решил переместить с одного конца гаража в другой. Здесь изменение местоположения сравнимо с размерами объекта. Поэтому каждая из точек автомобиля будет иметь разные координаты, а сам он рассматривается как объёмное тело в пространстве.
Видео:Уравнение движенияСкачать

Основные понятия
Следует учитывать, что для физика путь, пройденный определённым объектом, и перемещение – совсем не одно и то же, а эти слова не являются синонимами. Уяснить разницу между данными понятиями можно, рассмотрев движение самолёта в небе.
След, который он оставляет, наглядно показывает его траекторию, то есть линию. При этом путь представляет собой её длину и выражается в определённых единицах (к примеру, в метрах). А перемещение – это вектор, соединяющий лишь точки начала и конца движения.
Подобное можно увидеть на рисунке, приведённом ниже, который демонстрирует маршрут машины, едущей по извилистой дороге, и вертолёта, летящего по прямой. Векторы перемещения для этих объектов будут одинаковые, а пути и траектории – разными.
Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Равномерное движение по прямой
Теперь рассмотрим различные виды уравнений движения. И начнём с самого простого случая, когда некий объект перемещается по прямой с одинаковой скоростью. Это значит, что по истечении равных промежутков времени путь, который он проходит за данный период, не меняется по величине.
Что нам потребуется для описания данного движения тела, вернее, материальной точки, как уже было условлено его называть? Важно выбрать систему координат. Для простоты предположим, что перемещение происходит вдоль некоей оси 0Х.
Тогда уравнение движения: x = х0 + vхt. Оно и будет описывать процесс в общем виде.
Важным понятием при изменении местоположения тела является скорость. В физике она является векторной величиной, поэтому принимает положительное и отрицательное значение. Здесь всё зависит от направления, ведь тело может перемещаться по выбранной оси с возрастающей координатой и в противоположную сторону.
Видео:Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Относительность движения
Почему так важно выбрать систему координат, а также точку отсчёта для описания указанного процесса? Просто потому, что законы мироздания таковы, что без всего этого уравнение движения не будет иметь смысла. Это показано такими великими учёными, как Галилей, Ньютон и Эйнштейн. С начала жизни, находясь на Земле и интуитивно привыкнув выбирать её за систему отсчёта, человек ошибочно полагает, что существует покой, хотя для природы не бывает такого состояния. Тело может менять местоположение или оставаться статичным лишь относительно какого-либо объекта.
Мало того, тело может двигаться и находиться в покое одновременно. Примером тому может послужить чемодан пассажира поезда, который лежит на верхней полке купе. Он движется относительно деревни, мимо которой проезжает состав, и покоится по мнению своего хозяина, расположившегося на нижнем сидении у окна. Космическое тело, некогда получив начальную скорость, способно лететь в пространстве миллионы лет, пока не столкнётся с другим объектом. Движение его не будет прекращаться потому, что перемещается оно лишь относительно прочих тел, а в системе отсчёта, связанной с ним, космический путешественник находится в покое.
Видео:Кинематика. Закон движения. Урок 3Скачать

Пример составления уравнений
Итак, выберем за точку отсчёта некий пункт А, при этом координатной осью пусть будет для нас автомагистраль, находящаяся рядом. А направление её будет проходить с запада на восток. Предположим, что в эту же сторону в пункт В, расположенный за 300 км, пешком отправился путешественник со скоростью 4 км/ч.
Получается, что уравнение движения задаётся в виде: х = 4t, где t – время в пути. Согласно этой формуле, появляется возможность вычислить местонахождение пешехода в любой необходимый момент. Становится понятно, что через час он пройдёт 4 км, через два – 8 и достигнет пункта Б спустя 75 часов, так как его координата х = 300 окажется при t = 75.
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Если скорость отрицательна
Предположим теперь, что из В в А едет автомобиль, имея скорость 80 км/час. Здесь уравнение движения имеет вид: х = 300 – 80t. Это действительно так, ведь х0 = 300, а v = -80. Следует обратить внимание, что скорость в данном случае указывается со знаком «минус», потому что объект перемещается в отрицательном направлении оси 0Х. Через какое время автомобиль достигнет пункта назначения? Это произойдёт, когда координата примет нулевое значение, то есть при х = 0.
Остаётся решить уравнение 0 = 300 – 80t. Получаем, что t = 3,75. Это означает, что автомобиль достигнет пункта В через 3 часа 45 минут.
Необходимо помнить, что координата тоже может быть отрицательной. В нашем случае это оказалось бы, если б существовал некий пункт С, находящийся в западном направлении от А.
Видео:Решение графических задач на равномерное движениеСкачать

Движение с увеличением скорости
Перемещаться объект может не только с постоянной скоростью, но и менять её с течением времени. Движение тела может происходить по очень сложным законам. Но для простоты следует рассмотреть случай, когда ускорение увеличивается на определённое постоянное значение, а объект перемещается по прямой. В данном случае говорят, что это равноускоренное движение. Формулы, описывающие этот процесс, приведены ниже.
А теперь рассмотрим конкретные задачи. Допустим, что девочка, сев на санки на вершине горы, которую мы выберем за начало воображаемой системы координат с направлением оси по наклону вниз, начинает двигаться под действием силы тяжести с ускорением, равным 0,1 м/с 2 .
Тогда уравнение движения тела имеет вид: sx = 0,05t 2 .
Понимая это, можно узнать расстояние, которое девочка проедет на санках, для любого из моментов перемещения. Через 10 секунд это будет 5 м, а через 20 секунд после начала движения под гору путь составит 20 м.
Как выразить скорость на языке формул? Поскольку v0x = 0 (ведь санки начали катиться с горы без начальной скорости только под действием силы притяжения), то запись не будет слишком сложной.
Уравнение скорости движения примет вид: vx= 0,1t. Из него мы сможет узнать, как изменяется этот параметр с течением времени.
К примеру, через десять секунд vx= 1 м/с 2 , а через 20 с примет значение 2 м/с 2 .
Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Если ускорение отрицательно
Существует и другой вид перемещения, относящийся к тому же типу. Это движение называют равнозамедленным. В данном случае скорость тела тоже изменяется, но с течение времени не увеличивается, а уменьшается, и тоже на постоянную величину. Снова приведём конкретный пример. Поезд, ехавший до этого с постоянной скоростью 20 м/с, начал тормозить. При этом ускорение его составило 0,4 м/с 2 . Для решения примем за начало отсчёта точку пути поезда, где он начал тормозить, а координатную ось направим по линии его перемещения.
Тогда становится понятно, что движение задано уравнением: sx = 20t — 0,2t 2 .
А скорость описывается выражением: vx = 20 – 0,4t. Необходимо заметить, что перед ускорением ставится знак «минус», так как поезд тормозит, и данная величина отрицательна. Из полученных уравнений возможно заключить, что состав остановится через 50 секунд, проехав при этом 500 м.
Видео:Равномерное прямолинейное движение - физика 9Скачать

Сложное движение
Для решения задач в физике обычно создаются упрощённые математические модели реальных ситуаций. Но многогранный мир и явления, происходящие в нём, далеко не всегда вписываются в подобные рамки. Как составить уравнение движения в сложных случаях? Проблема решаема, ведь любой запутанный процесс возможно описать поэтапно. Для пояснения снова приведём пример. Вообразим, что при запуске фейерверков одна из ракет, взлетевшая с земли с начальной скоростью 30 м/с, достигнув верхней точки своего полёта, разорвалась на две части. При этом соотношение масс получившихся осколков составило 2:1. Далее обе части ракеты продолжили двигаться отдельно одна от другой таким образом, что первая полетела вертикально вверх со скоростью 20 м/с, а вторая сразу упала вниз. Следует узнать: какова была скорость второй части в момент, когда она достигла земли?
Первым этапом данного процесса окажется полёт ракеты вертикально вверх с начальной скоростью. Перемещение будет равнозамедленным. При описании понятно, что уравнение движения тела имеет вид: sx = 30t – 5t 2 . Здесь мы полагаем, что ускорение свободного падения для удобства округляется до значения 10 м/с 2 . Скорость при этом будет описываться следующим выражением: v = 30 – 10t. По этим данным уже возможно вычислить, что высота подъёма составит 45 м.
Вторым этапом движения (в данном случае уже второго осколка) окажется свободное падение этого тела с начальной скоростью, получаемой в момент распадения ракеты на части. При этом процесс будет равноускоренным. Для нахождения окончательного ответа сначала вычисляет v0 из закона сохранения импульса. Массы тел относятся 2:1, а скорости находятся в обратной зависимости. Следовательно, второй осколок полетит вниз с v0 = 10 м/c, а уравнение скорости примет вид: v = 10 + 10t.
Время падения мы узнаем из уравнения движения sx = 10t + 5t 2 . Подставим уже полученное значение высоты подъёма. В результате выходит, что скорость второго осколка приблизительно равна 31,6 м/с 2 .
Таким образом, разделяя сложное движение на простые составные части, можно решать любые запутанные задачи и составлять уравнения движения всех видов.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Механическое движение
О чем эта статья:
Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Видео:Физика. Решение задач. Уравнение движения тела,движущегося равномерно. Выполнялка 26Скачать

Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
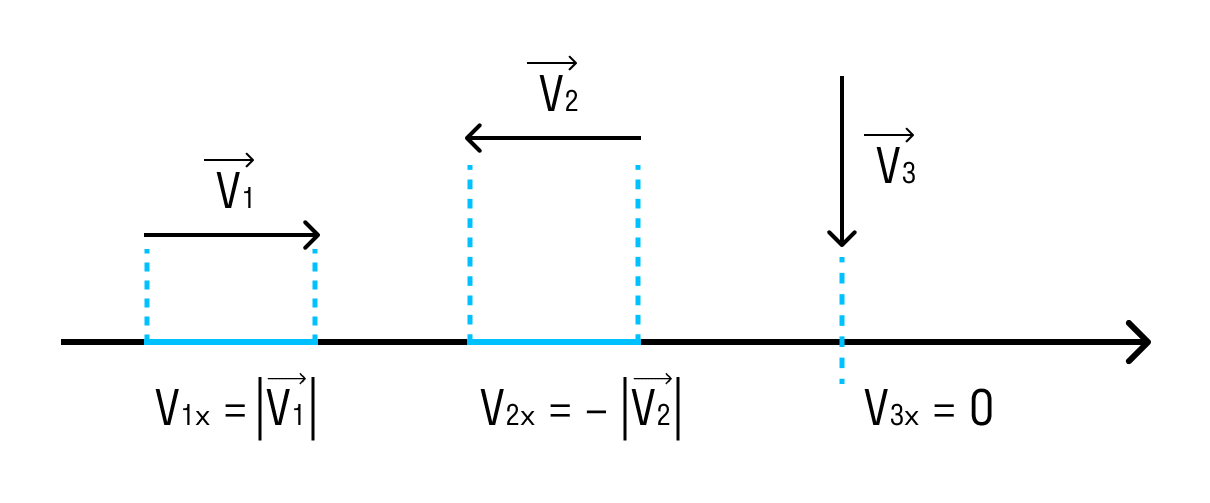
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Видео:Уравнение движения. Как найти время и место встречи двух тел ???Скачать

Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v