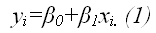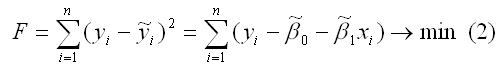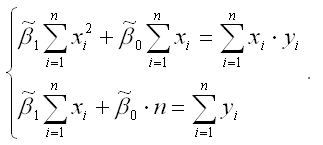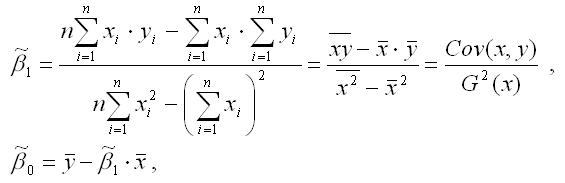Как составлять систему нормальных уравнений

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

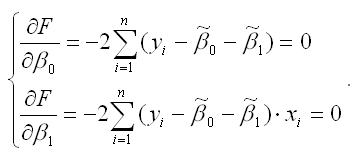
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

Видео:Решение систем уравнений методом подстановкиСкачать

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач

В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Нормальное уравнение прямой – описание и пример

Рассмотрим выведение нормального уравнения.

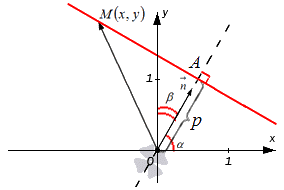
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.

Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .

O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .

Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p

Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y

Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.

Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.

Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.

Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .

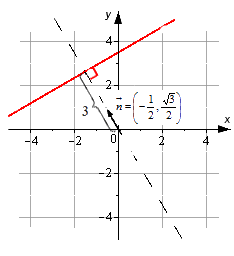
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Приведение общего уравнения прямой к нормальному виду

Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.

Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.

Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.

Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.

Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:

1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5

Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .

Нормальное уравнение по заданной прямой найдено.

Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Видео:Решение системы уравнений методом ГауссаСкачать

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Видео:Матричный метод решения систем уравненийСкачать

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

📺 Видео

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение систем уравнений методом сложенияСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Решение системы уравнений графическим методомСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Как написать уравнения касательной и нормали | МатематикаСкачать

Алгебра 7. Урок 8 - Системы линейных уравненийСкачать