Как составить векторное уравнение прямой

Видео:§48 Векторное уравнение прямой в пространствеСкачать

Общее уравнение прямой: описание, примеры, решение задач

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Общее уравнение прямой: основные сведения

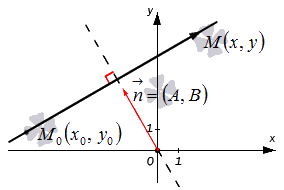
Пусть на плоскости задана прямоугольная система координат O x y .

Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .

указанная теорема состоит из двух пунктов, докажем каждый из них.

1. Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.

Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .

Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.

Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.

1. Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .

Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .

Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0

Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .

Рассмотрим конкретный пример общего уравнения прямой.

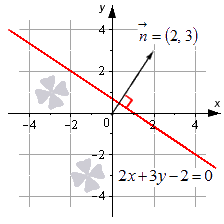
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Неполное уравнение общей прямой

Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.

Разберем все вариации неполного общего уравнения прямой.

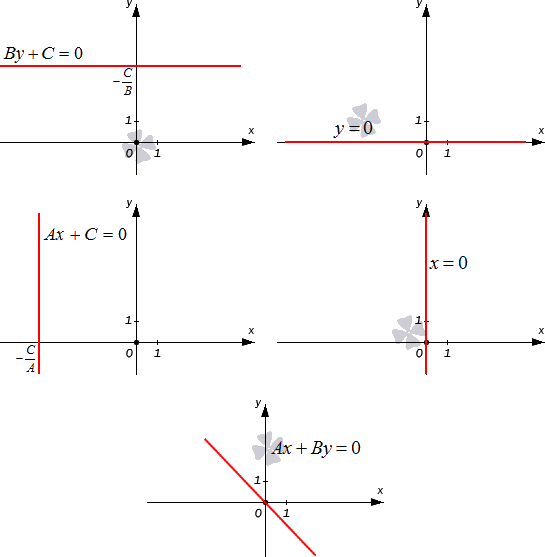
1. Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
2. Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
3. Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
4. Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
5. Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:

Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0

Ответ: 7 x — 2 = 0

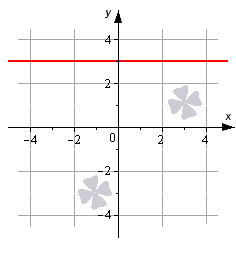
На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .

Ответ: y — 3 = 0 .

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:

A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0

Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .

Ответ: x — 2 · y + 11 = 0 .

Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

2 3 x 0 — y 0 — 1 2 = 0

Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2

Ответ: — 5 2

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .

Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .

Это равенство возможно записать как пропорцию: x + C A — B = y A .

В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .

Перепишем равенство в виде пропорции: x — B = y + C B A .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .

Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.

Ответ: x — 3 = y — 4 3 0 .

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Теперь примем обе части полученного канонического уравнения равными λ , тогда:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .

Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x

Ответ: y = — 2 7 x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.

Решение

Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Ответ: x — 1 2 + y 1 14 = 1 .

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0

Каноническое уравнение преобразуется к общему по следующей схеме:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0

Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.

Решение

Осуществим переход от параметрических уравнений к каноническому:

x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0

Перейдем от канонического к общему:

x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0

Ответ: y — 4 = 0

Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0

Ответ: 1 3 x + 2 y — 1 = 0 .

Видео:Параметрические уравнения прямойСкачать

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0

Ответ: 2 x — 3 y — 5 = 0 .

Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .

Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0

Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Уравнения прямых и плоскостей

Видео:§36 Векторные уравнения прямой на плоскостиСкачать

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть (A^+B^+C^ neq 0). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,label
$$
при условии (A^+B^ neq 0).

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения eqref и eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор (overrightarrow<M_M> = boldsymbol-boldsymbol_), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда (M) также лежит на прямой. В этом и только этом случае для точки (M) найдется такое число (t), что
$$
boldsymbol-boldsymbol_ = tboldsymbol.label
$$

Наоборот, какое бы число мы ни подставили в формулу eqref в качестве (t), вектор (boldsymbol) в этой формуле определит некоторую точку на прямой.

Уравнение eqref называется векторным параметрическим уравнением прямой, а переменная величина (t), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Получим теперь параметрические уравнения плоскости. Обозначим через (boldsymbol

) и (boldsymbol) ее направляющие векторы, а через (boldsymbol_) — радиус-вектор ее начальной точки (M_). Пусть точка (M) с радиус-вектором (boldsymbol) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор (overrightarrow<M_M> = boldsymbol-boldsymbol_), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец (M) также лежит на плоскости. Так как (boldsymbol

) и (boldsymbol) не коллинеарны, в этом и только этом случае (boldsymbol-boldsymbol_) может быть по ним разложен. Поэтому, если точка (M) лежит в плоскости (и только в этом случае), найдутся такие числа (t_) и (t_), что
$$
boldsymbol-boldsymbol_ = t_boldsymbol

+t_boldsymbol.label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров (t_) и (t_). Наоборот, какие бы числа мы ни подставили как значения (t_) и (t_), уравнение eqref определит некоторую точку плоскости.

Пусть ((x, y, z)) и ((x_, y_, z_)) — координаты точек (M) и (M_) соответственно, а векторы (boldsymbol

) и (boldsymbol) имеют компоненты ((p_, p_, p_)) и ((q_, q_, q_)). Тогда, раскладывая по базису обе части уравнения eqref, мы получим параметрические уравнения плоскости
$$
x-x_ = t_p_+t_q_, y-y_ = t_p_+t_q_, z-z_ = t_p_+t_q_.label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра (t), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Видео:11. Прямая в пространстве и ее уравненияСкачать

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой (M_(x_, y_)) и направляющим вектором (boldsymbol(a_, a_)) может быть записано в виде eqref.

Уравнение eqref линейное. Действительно, после преобразования оно принимает вид (a_x-a_y+(a_y_-a_x_) = 0), то есть (Ax+By+C = 0), где (A = a_), (B = -a_) и (C = a_y_-a_x_).

Вектор с координатами ((-B, A)) можно принять за направляющий вектор прямой с уравнением eqref в общей декартовой системе координат, а точку eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор (boldsymbol(A, B)) перпендикулярен прямой с уравнением eqref.

Действительно, в этом случае ((boldsymbol, boldsymbol) = -BA+AB = 0).

Пусть в уравнении прямой (Ax+By+C = 0) коэффициент (B) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,label
$$
где (k = -A/B), а (b = -C/B). Мы видим, что к равно отношению компонент направляющего вектора: (k = a_/a_) (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора (a_/a_) называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от (boldsymbol_) к (boldsymbol_) (рис. 6.4).

Рис. 6.4. (k=operatornamevarphi = -1). Прямая (y=-x+1/2)

Положив (x = 0) в уравнении eqref, получаем (y = b). Это означает, что свободный член уравнения (b) является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой (B = 0) и ее уравнение нельзя представить в виде eqref, то обязательно (A neq 0). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид (x = x_), где (x_ = -C/A) — абсцисса точки пересечения прямой с осью абсцисс.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

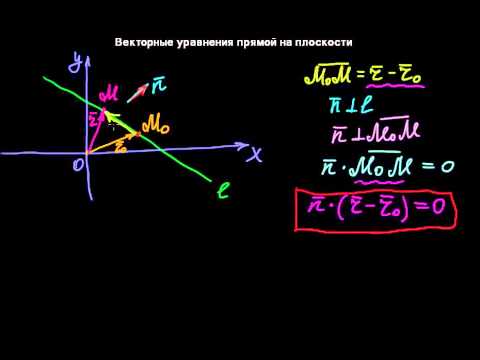
Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка (M) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки (M_) компланарна направляющим векторам (boldsymbol

) и (boldsymbol). Эту компланарность можно выразить и равенством
$$
(boldsymbol-boldsymbol_, boldsymbol

, boldsymbol) = 0.label
$$
Вектор (boldsymbol = [boldsymbol

, boldsymbol]) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение eqref в виде
$$
(boldsymbol-boldsymbol_, boldsymbol) = 0.label
$$

Уравнения eqref и eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в eqref (D = -(boldsymbol_, boldsymbol)), получим
$$
(boldsymbol, boldsymbol)+D = 0.label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные eqref и eqref,
$$
(boldsymbol-boldsymbol_, boldsymbol) = 0 mbox (boldsymbol, boldsymbol)+C = 0.nonumber
$$
Первое из них выражает тот факт, что вектор (boldsymbol-boldsymbol_) перпендикулярен ненулевому вектору (boldsymbol), перпендикулярному направляющему вектору (boldsymbol), и потому коллинеарен (boldsymbol).

Пусть (x, y, z) — компоненты вектора (boldsymbol) в общей декартовой системе координат. Тогда скалярное произведение ((boldsymbol-boldsymbol_, boldsymbol)) при (boldsymbol neq 0) записывается линейным многочленом (Ax+By+Cz+D), где ((A^+B^+C^ neq 0)).

Обратно, для любого линейного многочлена найдутся такие векторы (boldsymbol_) и (boldsymbol neq 0), что в заданной общей декартовой системе координат (Ax+By+Cz+D = (boldsymbol-boldsymbol_, boldsymbol)).

Первая часть предложения очевидна: подставим разложение вектора (boldsymbol) по базису в данное скалярное произведение:
$$
(xboldsymbol_+yboldsymbol_+zboldsymbol_-boldsymbol_, boldsymbol),nonumber
$$
раскроем скобки и получим многочлен (Ax+By+Cz+D), в котором (D = -(boldsymbol_, boldsymbol)) и
$$
A = (boldsymbol_, boldsymbol), B = (boldsymbol_, boldsymbol), C = (boldsymbol_, boldsymbol)label
$$
(A), (B) и (C) одновременно не равны нулю, так как ненулевой вектор (boldsymbol) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор (boldsymbol) из равенств eqref, считая (A), (B) и (C) заданными. Из ранее доказанного утверждения 10 следует, что
$$
boldsymbol = frac<A[boldsymbol_, boldsymbol_]><(boldsymbol_, boldsymbol_, boldsymbol_)>+frac<B[boldsymbol_, boldsymbol_]><(boldsymbol_, boldsymbol_, boldsymbol_)>+frac<C[boldsymbol_, boldsymbol_]><(boldsymbol_, boldsymbol_, boldsymbol_)>.label
$$

Вектор (boldsymbol_) должен удовлетворять условию (D = -(boldsymbol_, boldsymbol)). Один из таких векторов можно найти в виде (boldsymbol_ = lambda boldsymbol). Подставляя, видим, что (-lambda(boldsymbol, boldsymbol) = D), откуда (boldsymbol_ = -Dboldsymbol/|boldsymbol|^).

Итак, мы нашли векторы (boldsymbol) и (boldsymbol_) такие, что линейный многочлен записывается в виде
$$
x(boldsymbol_, boldsymbol)+y(boldsymbol_, boldsymbol)+z(boldsymbol_, boldsymbol)-(boldsymbol_, boldsymbol),nonumber
$$
который совпадает с требуемым ((boldsymbol-boldsymbol_, boldsymbol)).

Если система координат декартова прямоугольная, то вектор с компонентами (A), (B), (C) является нормальным вектором для плоскости с уравнением (Ax+By+Cz+D = 0).

Это сразу вытекает из формул eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, (alpha_, alpha_), должны быть пропорциональны компонентам — (B), (A) направляющего вектора прямой.

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0, A_x+B_y+C_ = 0,nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ = lambda A, B_ = lambda B.label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения eqref выполнено (с тем же (lambda)) равенство
$$
C_ = lambda C.label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами ((-B, A)) и ((-B_, A_)) — направляющие векторы прямых.

Докажем вторую часть. В равенствах eqref и eqref (lambda neq 0), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид (Ax+By+C = 0) и (lambda(Ax+By)+C_ = 0) при некотором (lambda). Если, кроме того, существует общая точка (M_(x_, y_)) обеих прямых, то (Ax_+By_+C = 0) и (lambda(Ax_+By_)+C_ = 0). Вычитая одно равенство из другого, получаем (C_ = lambda C), как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0, A_x+B_y+C_z+D_ = 0nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ = lambda A, B_ = lambda B, C_ = lambda C.label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений eqref выполнено (с тем же (lambda)) равенство
$$
D_ = lambda D.label
$$

Если плоскости параллельны, то их нормальные векторы (boldsymbol) и (boldsymbol_) коллинеарны, и существует такое число (lambda), что (boldsymbol_ = lambdaboldsymbol). В силу уравнений eqref (A_ = (boldsymbol_, boldsymbol_) = lambda(boldsymbol_, boldsymbol) = lambda A). Аналогично доказываются и остальные равенства eqref. Обратно, если равенства eqref выполнены, то из формулы eqref следует, что (boldsymbol_ = lambdaboldsymbol). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия eqref выражают не что иное, как коллинеарность векторов с компонентами ((A, B)) и ((A_, B_)). Точно так же условия eqref означают коллинеарность векторов с компонентами ((A, B, C)) и ((A_, B_, C_)). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
begin
A& B\
A_& B_
end
= 0,label
$$
а условие параллельности плоскостей — в виде
$$
begin
B& C\
B_& C_
end =
begin
C& A\
C_& A_
end =
begin
A& B\
A_& B_
end
= 0.label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии eqref система линейных уравнений
$$
Ax+By+C = 0, A_x+B_y+C_ = 0,nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от (C) и (C_). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
begin
A& B\
A_& B_
end
neq 0.nonumber
$$
то при любых (C) и (C_) система имеет единственное решение ((x, y)).

Видео:Видеоурок "Общие уравнения прямой"Скачать

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
left<begin
Ax+By+Cz+D = 0,\
A_x+B_y+C_z+D_ = 0.
endright.label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно eqref означает, что хоть один из детерминантов отличен от нуля:
$$
begin
B& C\
B_& C_
end^ +
begin
C& A\
C_& A_
end^ +
begin
A& B\
A_& B_
end^
neq 0.label
$$

Разумеется, систему eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = frac<x-x_><alpha_>, t = frac<y-y_><alpha_>, t = frac<z-z_><alpha_>,nonumber
$$
и мы получаем два равенства
$$
frac<y-y_><alpha_> = frac<z-z_><alpha_>, frac<x-x_><alpha_> = frac<z-z_><alpha_>,label
$$
или, в более симметричном виде,
$$
frac<x-x_><alpha_> = frac<y-y_><alpha_> = frac<z-z_><alpha_>,label
$$
Уравнения eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная (x)), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, (alpha_), то уравнения прямой принимают вид
$$
x = x_, frac<y-y_><alpha_> = frac<z-z_><alpha_>,label
$$
Эта прямая лежит в плоскости (x = x_) и, следовательно, параллельна плоскости (x = 0). Аналогично пишутся уравнения прямой, если в нуль обращается не (alpha_), а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, (alpha_) и (alpha_), то прямая имеет уравнения
$$
x = x_, y = y_.label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений eqref. По условию eqref один из детерминантов отличен от нуля. Допустим для определенности, что (AB_-A_B neq 0). В силу утверждения 9 при любом фиксированном (z) система уравнений будет иметь единственное решение ((x, y)), в котором (x) и (y), разумеется, зависят от (z). Они — линейные многочлены от (z): (x = alpha_z+beta_), (y = alpha_z+beta_).

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя (z) на (t), получаем параметрические уравнения прямой
$$
x = alpha_t+beta_, y = alpha_t+beta_, z = t.nonumber
$$

Первые две координаты начальной точки прямой (M_(beta_, beta_, 0)) можно получить, решая систему eqref при значении (z = 0).

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты ((alpha_, alpha_, 1)). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами ((A, B, C)) и (A_, B_, C_) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
begin
B& C\
B_& C_
end,
begin
C& A\
C_& A_
end,
begin
A& B\
A_& B_
end.label
$$

Вектор с компонентами eqref есть направляющий вектор прямой с уравнениями eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого ((alpha_, alpha_, alpha_)) удовлетворяют уравнению (Aalpha_+Balpha_+Calpha_ = 0), параллелен плоскости с уравнением (Ax+By+Cz+D = 0). Если, кроме того, он удовлетворяет уравнению (A_alpha_+B_alpha_+C_alpha_ = 0), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами eqref ненулевой в силу неравенства eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Уравнения прямой в пространстве векторное, общее, канонические, параметрические (Таблица)

Способ задания прямой в пространстве

Вид уравнения прямой

Векторное уравнение прямой, проходящей через точку М параллельно заданному вектору s .

s — направляющий вектор прямой

где t — скалярный множитель (параметр)

Канонические уравнения прямой, проходящей через точку M₀(x₀,y₀,z₀) и параллельно вектору s =

Параметрические уравнения прямой, проходящей через точку (x₀,y₀,z₀) параллельно вектору s = <m,n,p]

Прямая как линия пересечения двух непараллельных плоскостей (общие уравнения прямой)

💥 Видео

Каноническое уравнение прямой в пространстве. 11 класс.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Видеоурок "Нормальное уравнение прямой"Скачать

Уравнение прямой по двум точкамСкачать