Как составить уравнение высот треугольника зная уравнения его сторон (3 видео)

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Содержание

Примеры решений по аналитической геометрии на плоскости
Решения задач о треугольнике онлайн
Задача 17886 Даны две вершины A(3; -1), B(5; 7).
Условие
Решение
🎥 Видео

Видео:Уравнения стороны треугольника и медианыСкачать

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Видео:найти уравнение высоты треугольникаСкачать

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Видео:Уравнение прямой и треугольник. Задача про высотуСкачать

Задача 17886 Даны две вершины A(3; -1), B(5; 7).

Условие

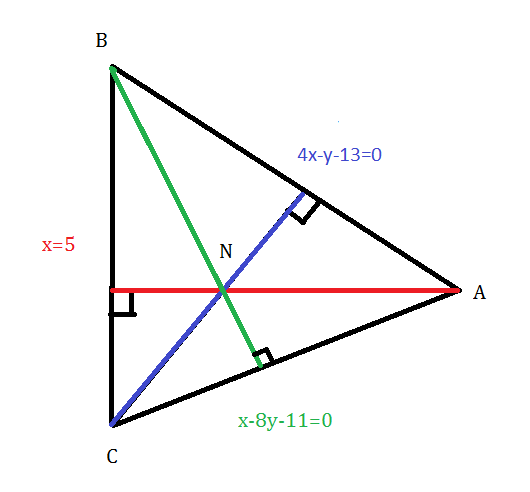
Даны две вершины A(3; -1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения его высот. Составить уравнения сторон этого треугольника.

Решение

Уравнение прямой АВ составим как уравнение прямой, проходящей через две точки:
(х-x_(A))/(x_(B)-x_(A))=(y-y_(A))/(y_(B)-y_(A))

Составим уравнение прямой AN

A(3; –1),N(4; –1)
Так как вторые координаты одинаковые, то значит прямая AN характеризуется тем свойством, что на ней расположены точки, у которых вторая координата равны -1.
Уравнение такой прямой имеет вид:
у=-1
Прямая ВС перпендикулярна прямой АN, значит уравнение этой прямой имеет вид
х=с ( с- константа)
Значит прямая ВС характеризуется тем свойством,что на ней расположены точки, у которых первая координата одинаковая.
Так как у точки В первая координата 5, то значит с=5
х=5 — уравнение прямой ВС.

Уравнение прямой ВN — уравнение прямой, проходящей через две точки:
(х-x_(B))/(x_(N)-x_(B))=(y-y_(B))/(y_(N)-y_(B))
(х-5)/(4-5)=(y-7)/(-1-7)
-8*(x-5)=-1*(y-7)
8x+y-47=0 — уравнение прямой BN.

Прямая АС перпендикулярна BN и проходит через точку А.

Если прямые у=k1x+b1 и y=k2x+b2 перпендикулярны, то
k1*k2=-1

y=(1/8)x+b — уравнение прямых, перпендикулярных BN.

Чтобы выделить из них прямую AC, подставим координаты точки А и найдем b.

y=(1/8)x-(11/8) или умножим на 8
8у=х-11

х-8у-11=0 — уравнение прямой АС

О т в е т.
4х-у-13=0 — уравнение прямой АВ
х-8у-11=0 — уравнение прямой АС
х=5 — уравнение прямой ВС