Как составить уравнение вектора по двум точкам (6 видео)

Содержание

Как составить уравнение вектора по двум точкам
Нахождение координат вектора через координаты точек
Упражнения на тему вычисления вектора по двум точкам на плоскости.
Правила. Вычисление вектора по двум точкам на плоскости.
🔍 Видео

Видео:Уравнение прямой по двум точкамСкачать

Как составить уравнение вектора по двум точкам

Неверно введено число.

Точки должны быть разными.

Уравнение прямой по двум точкам

Введите координаты точек:

Количество знаков после разделителя дроби в числах:

Общее уравнение прямой:

Теория

Уравнение прямой, проходящей через две заданные точки (x₁,y₁) и (x₂,y₂), имеет вид:

или в общем виде

Т.е. получили общее уравнение прямой линии на плоскости в декартовых координатах:

Видео:Составляем уравнение прямой по точкамСкачать

Нахождение координат вектора через координаты точек

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Упражнения на тему вычисления вектора по двум точкам на плоскости.

Эти упражнения позволят проверить, как вы умеете находить вектора по двум точкам на плоскости.

Решение задач и упражнений лучший способ проверить свои знания и закрепить пройденный материал!

Для перехода к следующему заданию нажмите кнопку «Следующий пример».

Внимание. При переходе к новому заданию этот пример станет недоступным.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Правила. Вычисление вектора по двум точкам на плоскости.

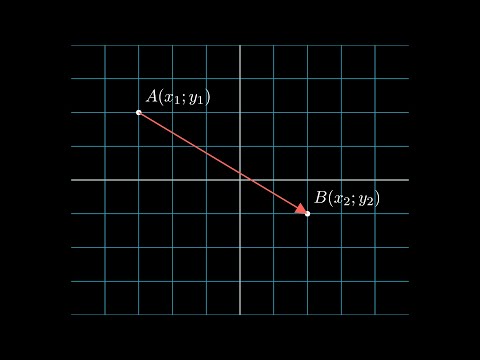
Чтобы на плоскости найти координаты вектора AB , зная координаты его начальной точки A( x ₁, y ₁) и конечной точки B( x ₂, y ₂), необходимо из координат конечной точки вычесть координаты начальной точки:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.