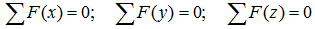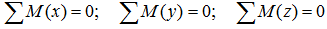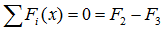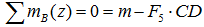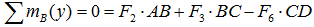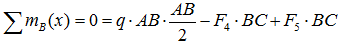Как составить уравнение равновесия для момента сил

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Видео:Определение реакций опор простой рамыСкачать

Пример составления уравнений равновесия

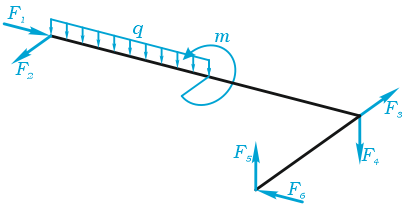
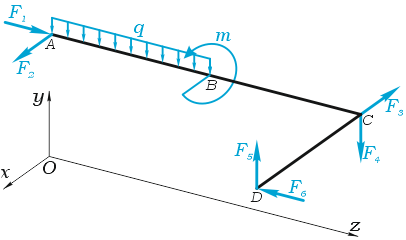
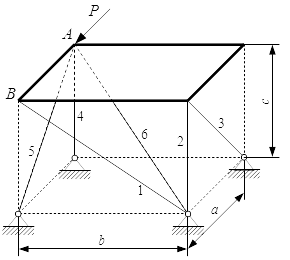
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

• в плоскости xOy:
  
• в плоскости xOz:
  
• в плоскости yOz:
  

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Равновесие произвольной пространственной системы сил – решение задачи

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Порядок решения задач на равновесие с произвольной пространственной системой сил

Чтобы решить задачу на равновесие твердого тела с произвольной пространственной системой сил, надо выбрать прямоугольную систему координат и, относительно нее, составить уравнения равновесия.

Уравнения равновесия, для произвольной системы сил, распределенных в трехмерном пространстве, представляют собой два векторных уравнения:
векторная сумма сил, действующих на тело, равна нулю
(1) ;
векторная сумма моментов сил, относительно начала координат, равна нулю
(2) .

Пусть Oxyz – выбранная нами система координат. Спроектировав уравнения (1) и (2) на оси этой системы, получим шесть уравнений:
суммы проекций сил на оси xyz равны нулю
(1.x) ;
(1.y) ;
(1.z) ;
суммы моментов сил относительно осей координат равны нулю
(2.x) ;
(2.y) ;
(2.z) .
Здесь мы считаем, что на тело действуют n сил, включая силы реакций опор.

Пусть произвольная сила , с компонентами , приложена к телу в точке . Тогда моменты этой силы относительно осей координат определяются по формулам:
(3.x) ;
(3.y) ;
(3.z) .

Таким образом, порядок решения задачи, на равновесие с произвольной пространственной системой сил, следующий.

1. Отбрасываем опоры и заменяем их силами реакций. Если опорой является стержень или нить, то сила реакции направлена вдоль стержня или нити.
2. Выбираем прямоугольную систему координат Oxyz .
3. Находим проекции векторов сил на оси координат, , и точек их приложения, . Точку приложения силы можно перемещать вдоль прямой, проведенной через вектор силы. От такого перемещения значения моментов не изменятся. Поэтому выбираем наиболее удобные для расчета точки приложения сил.
4. Составляем три уравнения равновесия для сил (1.x,y,z).
5. Для каждой силы, по формулам (3.x,y,z), находим проекции моментов силы на оси координат.
6. Составляем три уравнения равновесия для моментов сил (2.x,y,z).
7. Если число переменных больше числа уравнений, то задача статически неопределима. Методами статики ее решить нельзя. Нужно использовать методы сопротивления материалов.
8. Решаем полученные уравнения.

Упрощение расчетов

В некоторых случаях удается упростить вычисления, если вместо уравнения (2) использовать эквивалентное условие равновесия.
Сумма моментов сил относительно произвольной оси AA′ равна нулю:
(4) .

То есть можно выбрать несколько дополнительных осей, не совпадающих с осями координат. И относительно этих осей составить уравнения (4).

Далее приводится пример, в котором удается упростить вычисления за счет соответствующего выбора осей.

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Пример решения задачи на равновесие произвольной пространственной системы сил

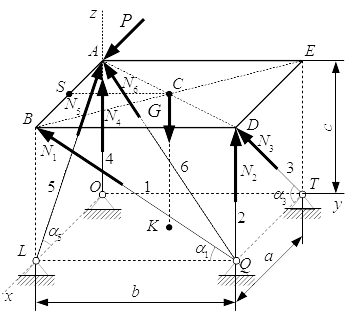
Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве. Система крепления стержней показана на рисунке. На плиту действуют: сила тяжести G; и сила P, приложенная в точке A, направленная вдоль стороны AB.

Дано:
G = 28 kН ; P = 35 kН ; a = 7,5 м ; b = 6,0 м ; c = 3,5 м .

Решение задачи

Сначала мы решим эту задачу стандартным способом, применимым для произвольной пространственной системы сил. А затем получим более простое решение, основываясь на конкретной геометрии системы, за счет выбора осей при составлении уравнений равновесия.

Решение задачи стандартным способом

Этот метод хоть и приведет нас к довольно громоздким вычислениям, но он применим для произвольной пространственной системы сил, и может применяться в расчетах на ЭВМ.

Отбросим связи и заменим их силами реакций. Связями здесь являются стержни 1–6. Вводим вместо них силы , направленные вдоль стержней. Направления сил выбираем наугад. Если мы не угадаем с направлением какой-либо силы, то получим для нее отрицательное значение.

Проводим систему координат Oxyz с началом в точке O .

Находим проекции сил на оси координат.

Для силы имеем:
.
Здесь α ₁ – угол между LQ и BQ . Из прямоугольного треугольника LQB :
м ;
;
.

Силы , и параллельны оси z . Их компоненты:
;
;
.

Для силы находим:
.
Здесь α ₃ – угол между QT и DT . Из прямоугольного треугольника QTD :
м ;
;
.

Для силы :
.
Здесь α ₅ – угол между LO и LA . Из прямоугольного треугольника LOA :
м ;
;
.

Сила направлена по диагонали прямоугольного параллелепипеда. Она имеет следующие проекции на оси координат:
.
Здесь – направляющие косинусы диагонали AQ :
м ;
;
;
.

Выбираем точки приложения сил. Воспользуемся тем, что их можно перемещать вдоль линий, проведенных через векторы сил. Так, в качестве точки приложения силы можно взять любую точку на прямой TD . Возьмем точку T , поскольку для нее x и z — координаты равны нулю:
.
Аналогичным способом выбираем точки приложения остальных сил.

В результате получаем следующие значения компонентов сил и точек их приложений:
; (точка B );
; (точка Q );
; (точка T );
; (точка O );
; (точка A );
; (точка A );
; (точка A );
; (точка K ).

Составляем уравнения равновесия для сил. Суммы проекций сил на оси координат равны нулю.

;

;

.

Составляем уравнения равновесия для моментов сил. Суммы моментов сил относительно осей координат равны нулю.

;

;

;

В этой системе шесть уравнений и шесть неизвестных. Далее сюда можно подставить численные значения и получить решение системы, используя математическую программу вычисления системы линейных уравнений.

Но, для этой задачи, можно получить решение без использования средств вычислительной техники.

Эффективный способ решения задачи

Мы воспользуемся тем, что уравнения равновесия можно составлять не единственным способом. Можно произвольным образом выбирать систему координат и оси, относительно которых вычисляются моменты. Иногда, за счет выбора осей, можно получить уравнения, которые решаются более просто.

Воспользуемся тем, что, в равновесии, сумма моментов сил относительно любой оси равна нулю. Возьмем ось AD . Сумма моментов сил относительно этой оси равна нулю:
(П7) .
Далее заметим, что все силы, кроме пересекают эту ось. Поэтому их моменты равны нулю. Не пересекает ось AD только одна сила . Она также не параллельна этой оси. Поэтому, чтобы выполнялось уравнение (П7), сила N ₁ должна равняться нулю:
N ₁ = 0 .

Теперь возьмем ось AQ . Сумма моментов сил относительно нее равна нулю:
(П8) .
Эту ось пересекают все силы, кроме . Поскольку сила не параллельна этой оси, то для выполнения уравнения (П8) необходимо, чтобы
N ₃ = 0 .

Теперь возьмем ось AB . Сумма моментов сил относительно нее равна нулю:
(П9) .
Эту ось пересекают все силы, кроме , и . Но N ₃ = 0 . Поэтому
.
Момент от силы относительно оси равен произведению плеча силы на величину проекции силы на плоскость, перпендикулярную оси. Плечо равно минимальному расстоянию между осью и прямой, проведенной через вектор силы. Если закручивание происходит в положительном направлении, то момент положителен. Если в отрицательном – то отрицательный. Тогда
.
Отсюда
kН .

Остальные силы найдем из уравнений (П1), (П2) и (П3). Из уравнения (П2):
N ₆ = 0 .
Из уравнений (П1) и (П3):
kН ;
kН

Таким образом, решая задачу вторым способом, мы использовали следующие уравнения равновесия:
;
;
;
;
;
.
В результате мы избежали громоздких расчетов, связанных с вычислениями моментов сил относительно осей координат и получили линейную систему уравнений с диагональной матрицей коэффициентов, которая сразу разрешилась.

N ₁ = 0 ; N ₂ = 14,0 kН ; N ₃ = 0 ; N ₄ = -2,3 kН ; N ₅ = 38,6 kН ; N ₆ = 0 ;

Знак минус указывает на то, что сила N ₄ направлена в сторону, противоположную той, которая указана на рисунке.

Автор: Олег Одинцов . Опубликовано: 13-11-2017

Видео:Определение реакций опор в балке. Сопромат.Скачать

Условия и уравнения равновесия твердого тела: плоской и пространственной системы сил

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Условия равновесия произвольной системы сил

Еще Ньютон говорил, что если геометрическая сумма сил, действующая на тело, равна нулю, то тело:

• либо находится в состоянии покоя;
• либо движется равномерно прямолинейно.

Из теоретической механики известно, что действие нескольких сил, просуммировав, можно заменить равнодействующей силой:

Тогда обязательное условие равновесия можно записать так:

Однако для полного равновесия, часто, этого условия недостаточно, если тело имеет возможность вращаться относительно какой-то точки или оси, то для равновесия такой системы, необходимо, чтобы выполнялось условие:

где M — главные момент системы, который эквивалентен сумме моментов системы относительно некоторого центра.

Видео:Урок 76. Задачи на правило моментовСкачать

Условия равновесия плоской системы сил

Выше описанные условия означают, что система будет находится в равновесии, когда все силы, действующие на систему, будут взаимно уравновешиваться и момент относительно любой произвольной точки будет равен нулю, отсюда вытекает первая и основная форма условий равновесия для плоской системы сил:

Вторая форма условий равновесия записывается следующим образом:

Важно! Ось не должна быть перпендикулярна прямой AB.

И, наконец, третья форма условий равновесия выглядит так:

Из данной системы уравнений следует, что для равновесия системы достаточно равенства нулю суммы моментов относительно трех точек.

Важно! Точки, относительно которых записываются уравнения не должны лежать на одной прямой.

Видео:Определение реакций опор простой рамыСкачать

Уравнения равновесия для плоской системы сил

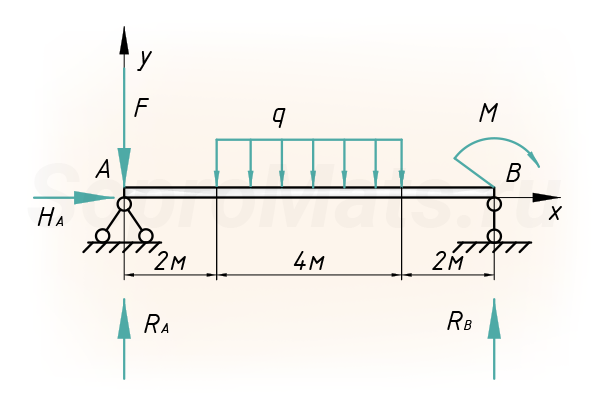
Рассмотрим на примере плоской балки, как записываются уравнения равновесия. Использовать будет классическую (первую) форму условия равновесия:

Сумма моментов относительно точки A:

Сумма проекций всех сил на вертикальную ось (y):

Сумма проекций всех сил на горизонтальную ось(x):

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Условие равновесия пространственной системы сил

Для пространственной системы сил условие равновесие выглядит вот так:

Таким образом, пространственная система будет находиться в равновесии, если суммы проекций сил на координатные оси, а также суммы моментов относительно осей будут равны нулю.

Видео:Урок 70. Виды равновесия. Условие равновесия тела при отсутствии вращения.Скачать

Уравнения равновесия для пространственной системы сил

В качестве примера рассмотрим пространственную раму, закруженную сосредоточенными силами. Составим для нее шесть уравнений равновесия:

📹 Видео

§ 5.3. Уравнения равновесия плоской системы силСкачать

Физика 10 класс (Урок№14 - Статика. Равновесие абсолютно твердых тел.)Скачать

Урок 80 (осн). Момент силы. Правило моментовСкачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Условия равновесия систем силСкачать

§ 5.5. Уравнения равновесия системы сходящихся силСкачать

Равновесие тел. Условие равновесия тел. Центр масс и центр тяжести. Практическая часть. 10 класс.Скачать

определение реакций в стержнях от действия грузовСкачать

Три формы уравнений равновесия произвольной плоской системы силСкачать

Момент силы относительно точки и осиСкачать