- Зачем это нужно?
- Минимизация логических функций при помощи карт Карно
- Порядок работы с картой Карно
- Электростанции
- Навигация
- Меню раздела
- Метод карт Карно
- Карта Карно для двух переменных
- Карта Карно для трех переменных
- Карта Карно для четырех переменных
- Карта Карно для пяти переменных
- Карта Карно для более чем пяти переменных
- 💡 Видео
Зачем это нужно?
Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.
В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.
Минимизация логических функций при помощи карт Карно
Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
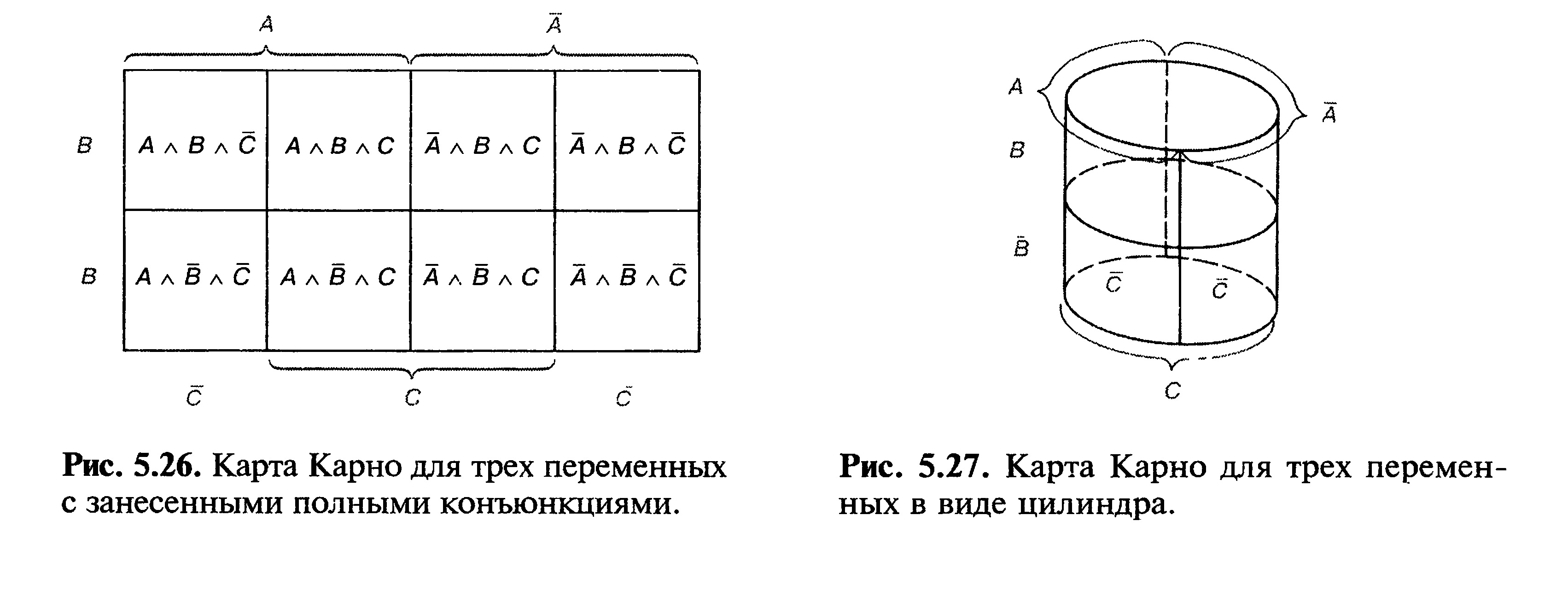
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
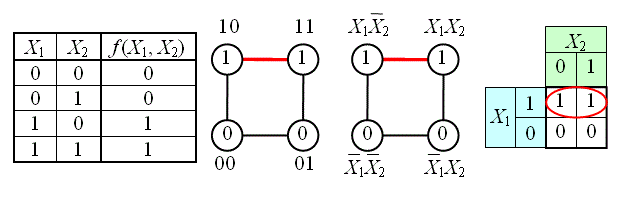
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
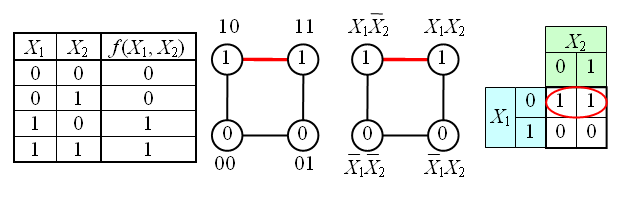
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных: 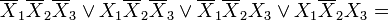
В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.
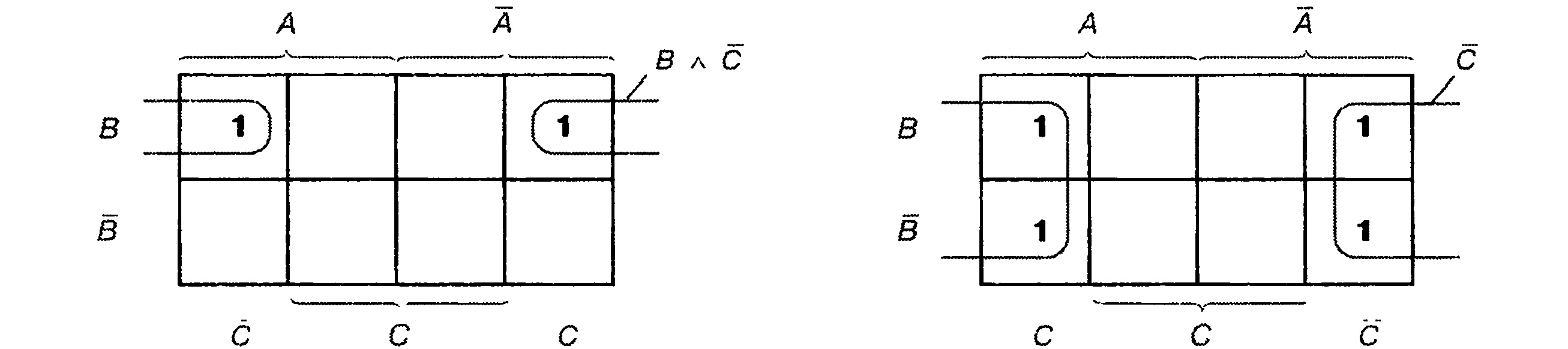
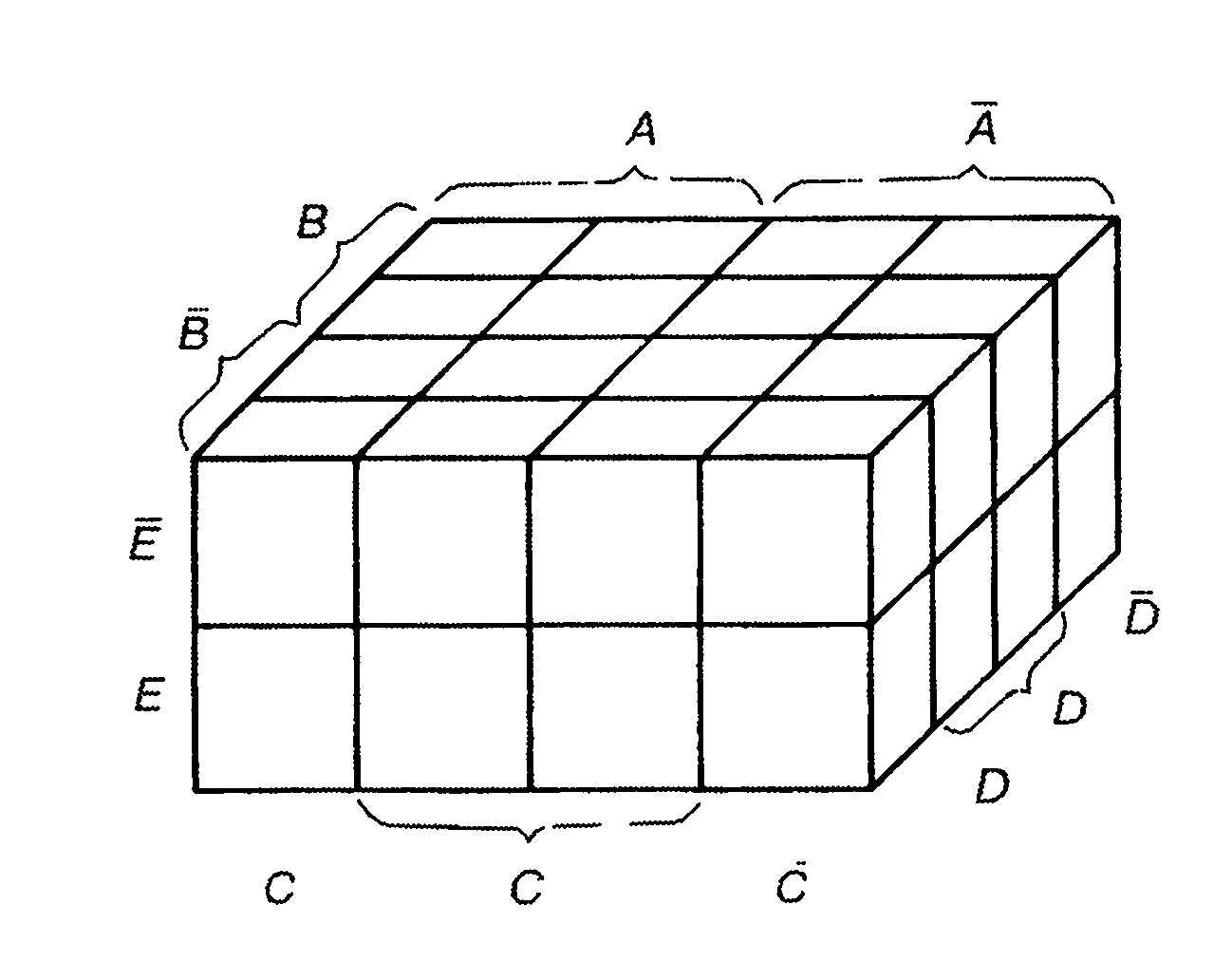
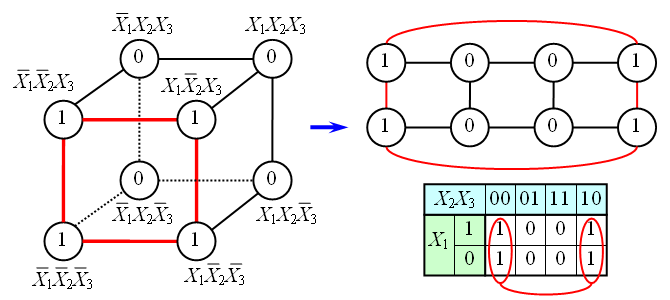
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.
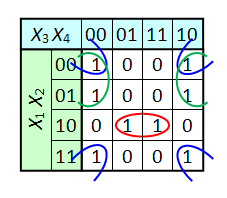
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
- Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…
) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
- Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
- Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
- Область должна быть как можно больше, а кол-во областей как можно меньше;
- Области могут пересекаться;
- Возможно несколько вариантов накрытия.
Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):
Видео:Лекция 80. Карта КарноСкачать

Порядок работы с картой Карно
Лекция №11
Упрощение логических выражений методом карт Карно
2. Принцип минимизации.
3. Порядок работы с картой Карно.
Куб Карно
Куб Карно́ — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом
Принцип минимизации
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2 N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Таблица не верна. Верной будет: 1 1 0 0 1 1 0 0. Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:
В общем случае можно сказать, что 2 K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом, появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Аналогичным образом можно работать с функциями пяти, семи (обязательно простое число) и т.д., используя не визуализируемые многомерные булевы кубы.
Порядок работы с картой Карно
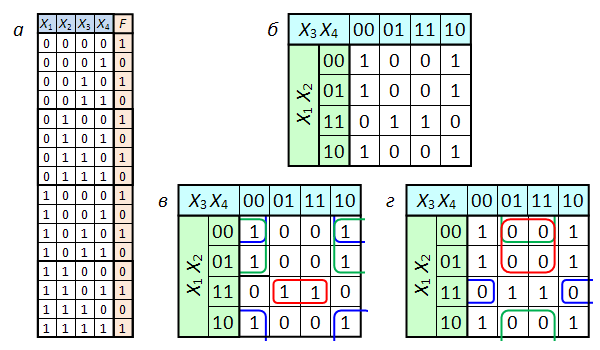
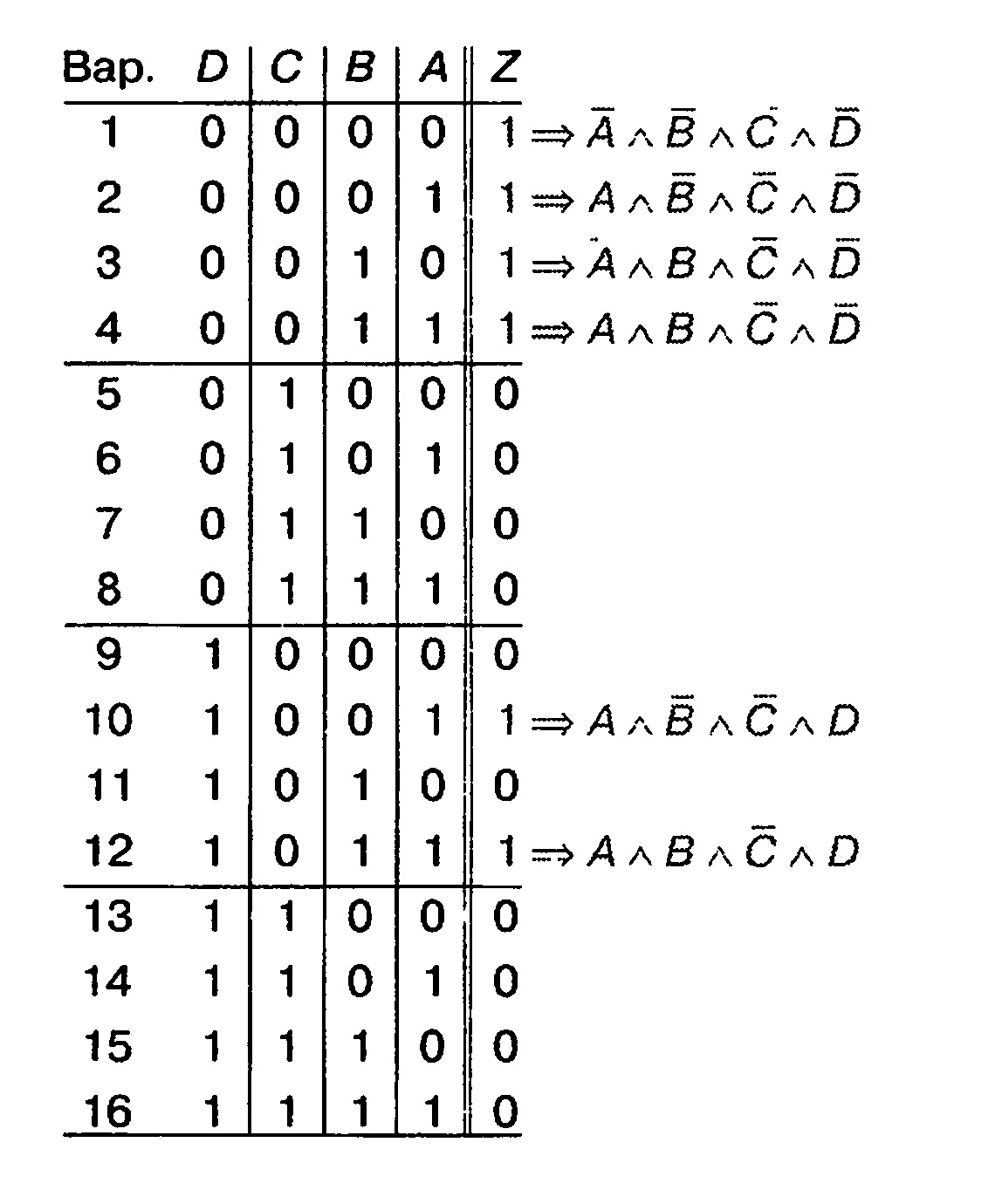
Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2 N наборах входных переменных X1 . XN. Карта Карно также содержит 2 N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 . XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.
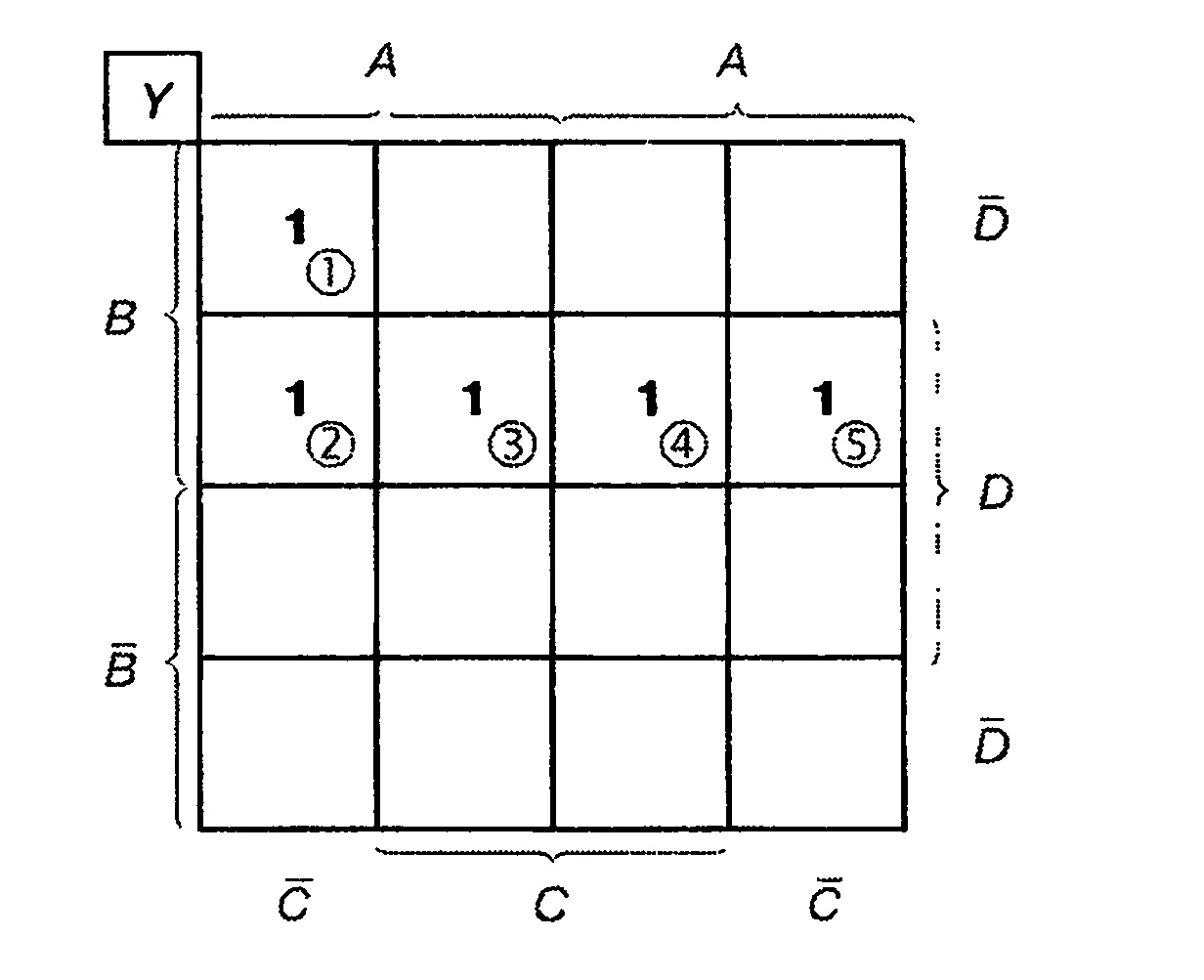
В данном разделе в качестве примера используется функция четырёх переменных, заданная таблицей истинности, изображённой на рис. 2а. Карта Карно для той же функции изображена на рис. 2б.
Рис. 2. Пример работы с картой Карно
Принципы склейки
· Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить ДНФ) или по нулям (если требуется КНФ).
· Склеивать можно только прямоугольные области с числом единиц (нулей) 2 n , где n — целое число. Для карт Карно с числом переменных более четырёх могут получаться более сложные области, о чём будет сказано в следующих разделах.
· Область, которая подвергается склейке должна содержать только единицы (нули).
· Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой (топологически карта Карно для четырёх переменных представляет собой тор) и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули) они могут быть объединены в квадрат, как показано на рис. 2в.
· Все единицы (нули) должны попасть в какую-либо область.
· С точки зрения минимальности ДНФ (КНФ) число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм. Терм размером 2 n ячеек содержит N–n переменных).
· Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:
· В отличие от СДНФ (СКНФ), ДНФ (КНФ) не единственны. Возможно несколько эквивалентных друг другу ДНФ (КНФ), которые соответствуют разным способам покрытия карты Карно прямоугольными областями.
Описание
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути, Карта Карно — это таблица истинности, составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.е. вся Карта Карно сворачивается в фигуру тор (бублик) (рис.4.1).
Рис. 4.1. Метод скручивания карты Карно
На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала 


2. Область должна располагаться симметрично оси (ей) (оси располагаются через каждые четыре клетки);
3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну;
4. Область должна быть как можно больше, а количество областей как можно меньше;
5. Области могут пересекаться;
6. Возможно несколько вариантов покрытия.
Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например (для Карт на 2 переменные):
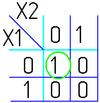 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
 |  |  |  |  |  | ||
 |  |  |  |  |  | ||
 | 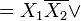 |  |  |  |  | ||
 |  |
Для КНФ всё то же самое, только рассматриваем клетки с нулями, неменяющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид:
Так же из ДНФ в КНФ и обратно можно перейти использовав Законы де Моргана.
Пример 1.
Упростить полученную СДНФ, используя склеивание, а так же применить карту Карно для получения ДНФ.


Дизъюнкции в скобках получены по парам наборов переменных (0,0,0), (0,0,1) и (0,0,0), (0,1,0). Наборы в каждой паре отличаются только в одной позиции и называются соседними. После упрощения остаются совпадающие в паре переменные. Карты Карно представляют собой таблицу истинности, в которой соседние наборы переменных расположены рядом (метод скользящей единицы при этом нарушается).
Для нашей функции имеем
Карты Карно позволяют получить ДНФ минимальную по числу переменных или их отрицаний. Для этого необходимо заключить в круги рядом стоящие значения функции равные 1, причём
1) Каждый руг может содержать только 2 K (к = 0, 1, 2,…) единиц, например16, 8, 4, 2, 1.
2) Круги должны быть наибольшего размера.
3) Число кругов наименьшее, покрывающее все единицы.
4) Так как наборы (0,0) и (1,0) соседние. То края карты соединяются друг с другом.
5) По каждому из кругов составляется простая конъюнкция, входящая в ДНФ. При этом оставляются только те переменные, которые сохраняют свое значение во всем круге и как обычно, если хi = 1, то пишем хi , если хi = 0, то 
Построим круги для нашего примера.
yz  x x | |
| 1 1 | 1 2 |
Имеем две конъюнкции. Для первого круга 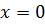


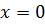



Пример 2
У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять на улицу, если ему разрешат хотя бы двое родственников.
Для краткости обозначим родственников Коли через буквы:
мама — х1
папа — х2
дедушка — х3
бабушка — х4
Условимся обозначать согласие родственников единицей, несогласие — нулём. Возможность пойти погулять обозначим буквой f, Коля идёт гулять — f = 1, Коля гулять не идёт — f = 0.
Составим таблицу истинности:
Перерисуем таблицу истинности в 2-х мерный вид:
Переставим в ней строки и столбцы в соответствии с кодом Грея. Получили Карту Карно:
Заполним её значениями из таблицы истинности:
Минимизируем в соответствии с правилами:
1. 1. Все области содержат 2^n клеток;
2. 2. Так как Карта Карно на четыре переменные, оси располагаются на границах Карты и их не видно (подробнее смотри пример Карты на 5 переменных);
3. 3. Так как Карта Карно на четыре переменные, все области симметрично осей — смежные между собой (подробнее смотри пример Карты на 5 переменных);
4. 4. Области S3, S4, S5, S6 максимально большие;
5. 5. Все области пересекаются (необязательное условие);
6. 6. В данном случае рациональный вариант только один.
Теперь по полученной минимальной ДНФ можно построить логическую схему:
Из-за отсутствия в наличии шести — входового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы (D7, D8).
Составим мин. КНФ:
Для минимизации логических функций возможно использовать разные методы:
- карта Карно (Вейча)
- Квайна
- Квайна- Мак-Класки
- Петрика
Отличие метода карт Карно от карт Вейча заключается в способе обозначения строк и столбцов карт. У карт Карно строки и столбцы обозначаются с помощью кода Грея. Однако, принципиальной разницы между ними нет.
Метод минимизационных карт Карно (или карт Вейча) хорошо работает при числе аргументов 3,4 и даже 5 и обеспечивает простоту получения результата. Этот метод основан на зрительном анализе таблиц (карт) и не может быть применен для обработки вычислительной техникой.
1. Минимизировать нижеприведённые функции, представленные картами Карно.
Не заполненные клетки соответствуют нулю. Переменные, обозначенные буквами, соответствуют прямому значению, а не обозначенные — инверсному.
1. Определение куба Карно.
2. Кем и в каком году были изобретены карты Карно?
3. Основной метод минимизации логических функций?
4. Принципы склейки карты Карно.
5. В какую фигуру сворачивается карта Карно?
Видео:Построение минимальной ДНФ. Карты КарноСкачать

Электростанции
Видео:Минимизация функций. Карты Карно. Цифровая техникаСкачать

Навигация
- Меню сайта
- Организация эксплуатации
- Электрические схемы
- Турбогенераторы
- Трансформаторы и автотрансформаторы
- Распределительные устройства
- Электродвигатели
- Автоматика
- Тепловая изоляция
- Регулирование энергоблоков
- Тяговые подстанции
- Выпрямители и зарядные устройства
- Проектирование электрических сетей и систем
- Электрооборудование электротермических установок
- Электрооборудование земснарядов
- Цифровая электроника
Видео:Карты Карно. Как они работают. Большой выпуск.Скачать

Меню раздела
Видео:Что такое карты Карно? Душкин объяснитСкачать

Метод карт Карно
Метод карт Карно служит для наглядного представления и упрощения нормальной формы ИЛИ. Он был придуман математиком Карно, и его еще называют методом диаграмм Карно.
Карта Карно для двух переменных
Карты Карно могут быть представлены в виде таблиц истинности для полных конъюнкций.
3—2114
Карты Карно всегда имеют количество полей, равное количеству возможных полных конъюнкций.
При двух переменных возможны 4 полные конъюнкции. Таким образом, карта Карно для двух переменных должна иметь 4 поля (см. рис. 5.12). По краям карты записываются переменные. Каждая переменная величина должна быть представлена в инвертированной и в неинвертированной форме (рис. 5.12).
Переменные по краям являются координатной сеткой. Они определяют, какая полная конъюнкция какому полю принадлежит. На рис. 5.13 по своим полям расписаны 4 полных конъюнкции.
Поле полной конъюнкции А а В обозначено координатами А и В
(рис. 5.13). Соответственно поле полной конъюнкции А а В находится по
координатам А и В. Так как полные конъюнкции определяются координатами, то нет необходимости записывать их в полной форме, как на рис. 5.13. Наличие полной конъюнкции может обозначаться 1 в соответствующем поле.
1 в поле карты Карно означает наличие полной конъюнкции.
На карте Карно (рис. 5.14) отмечены полные конъюнкции А а В и А а В. Карта Карно отражает следующую нормальную форму ИЛИ:
Z = (AaB)v(AaB).
Символ Z в верхнем левом углу карты на рис. 5.14 показывает, что полные конъюнкции относятся к Z.
Отсутствующие полные конъюнкции обозначены нулем в соответствующем поле, или поле не заполняется.
Присваивание переменных координатам карты Карно производится произвольным образом.
Также возможно менять местами А и В на карте (рис. 5.15). Разумеется, переменные могут иметь совершенно другие обозначения, например Ег и Ег Прямое и инверсное значения переменной должны обязательно находиться на одной стороне карты.
Другое распределение координатных переменных ведет, естественно, к другому распределению полных конъюнкций по полям карты.
Желательно придерживаться определенной схемы распределения переменных и не менять ее без причины. Для облегчения работы рекомендуется первую переменную, например А, и ее инверсию все время ставить на верхнюю часть карты. Вторую переменную (например В) и ее инверсию ставить на левую часть карты.
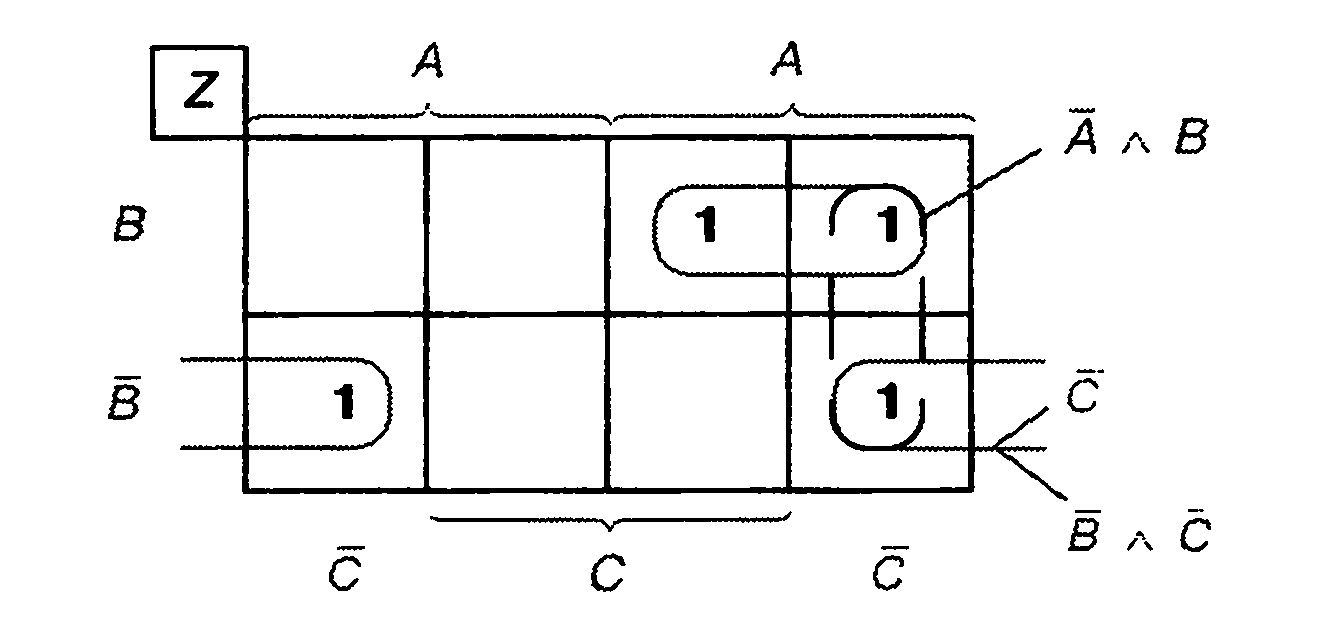
Покажем на примере заполнение карты Карно нормальной формой ИЛИ и восстановление нормальной формы ИЛИ по карте Карно.
Пример 1
Занесите в карту Карно нормальную форму ИЛИ:
Z = (Л л В) v (А л В) v (Л а В).
Сначала нужно нарисовать карту Карно с данными координатами. Затем найти поля с полными конъюнкциями, присутствующими в нормальной форме и обозначить их 1. Результат показан на рис. 5.16.
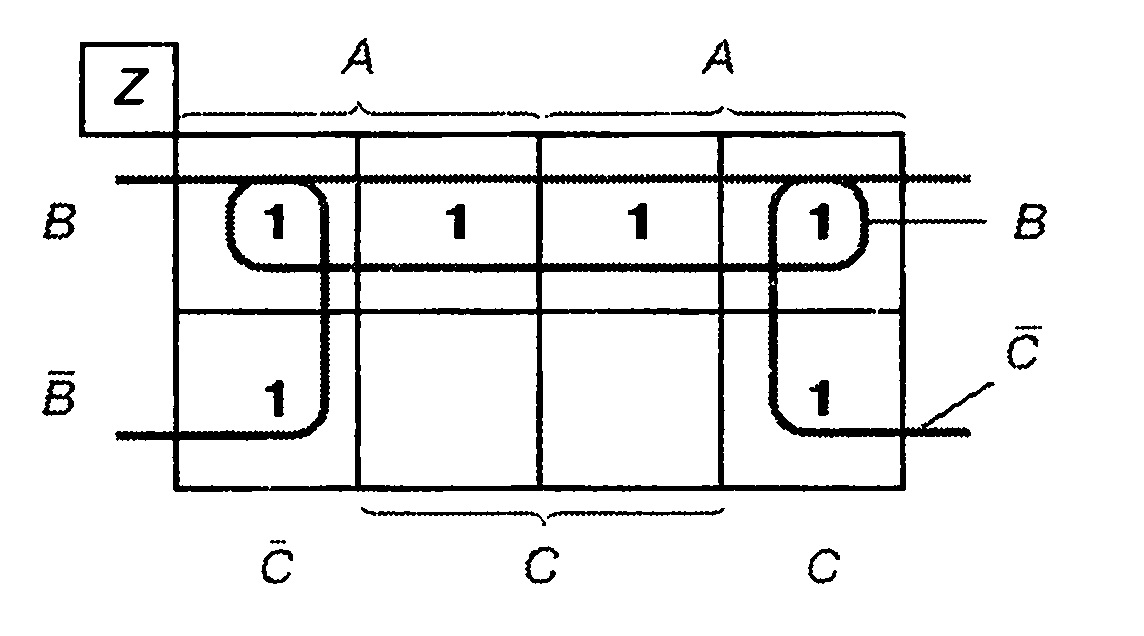
Пример 2—————————————————————
Запишите нормальную форму ИЛИ, представленную на карте Карно (рис. 5.17).
Нормальная форма ИЛИ содержит 2 полные конъюнкции: одна А д В, вторая АлВ. Следовательно, нормальная форма:
W = (АлВ)ч(АлВ).
Представленная на карте Карно нормальная форма ИЛИ может быть упрощена при наличии определенных условий.
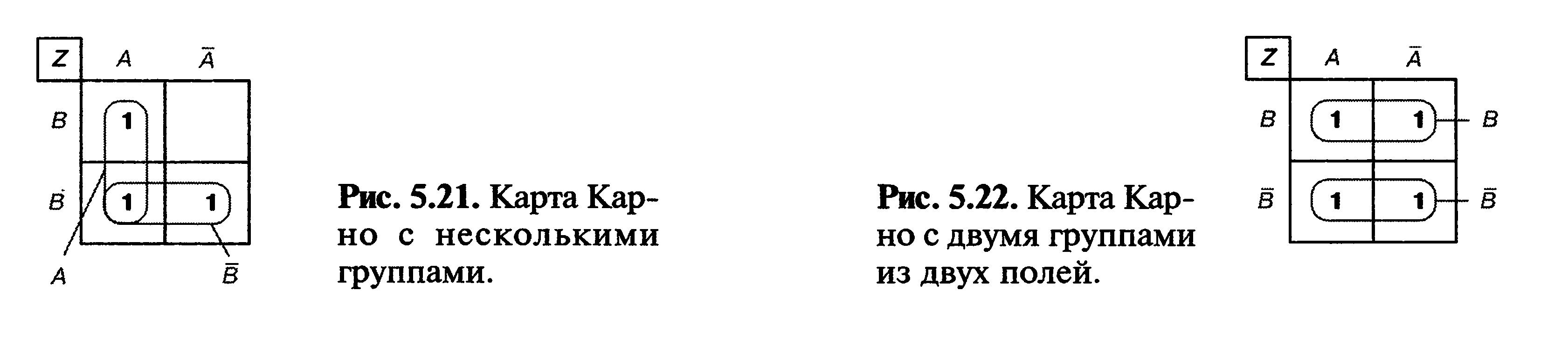
«Соседние» полные конъюнкции можно объединять в «группы».
Соседними считаются полные конъюнкции, клетки которых имеют общие стороны (рис. 5.18). Если клетки с полными конъюнкциями имеют только общий угол, то они не являются соседними.
Рис. 5.18. Соединение и несоединение конъюнкции
В одной группе могут быть объединены 2 или 4 соседние полные конъюнкции.
Каждая группа имеет определенные координаты. Группа слева наверху на карте Карно (рис. 5.18) имеет по одной стороне координату Д по другой —
координату А и А.
Содержание группы характеризуется ее координатами. Переменные, чьи координаты присутствуют в прямой и инверсной форме одновременно, исключаются.
Представленная на рис. 5.19 группа имеет координаты А, В ж В. Переменная В имеет как прямую, так и инверсную формы. Следовательно, она исключается. Значение группы будет А. Нормальная форма ИЛИ
Это упрощение может быть проверено с помощью алгебры логики.
Особый случай представляет группа из 4 полных конъюнкций (рис. 5.20).
Она имеет координаты А, А, В, В. Значит, переменные Аж В исключаются. Значение группы равно 1. Справедливость этого можно доказать с помощью таблицы истинности. Алгебра логики также приведет к этому результату:
Z = (А а В) v (А а В^ v (А а В> v [А а В^;
Z = [А а (В v 5)] v _А а (В v 5)];
Z = (AaI)v(AaI);
Z = Av А;
Z = l.
На одной карте можно образовать несколько групп (рис. 5.21). Одна полная конъюнкция может присутствовать в нескольких группах.
При наличии нескольких групп упрощенное уравнение получается в результате логического сложения значений отдельных групп.
Для карты (рис. 5.21) значения групп получаются равными А и В.
Упрощенное уравнение:
Z = AvB.
На карте Карно (рис. 5.20) можно образовать также две группы из двух полей. Тогда получится упрощенное уравнение, но не в самом простом виде. Покажем это. На рис. 5.22 показана карта Карно с такой группировкой. Значения групп равны В ж В. Упрощенное уравнение, следовательно:
Z = Bv В.
Сложение переменной величины с ее инверсией дает в итоге по правилам алгебры логики 1. Поэтому самой простой формой уравнения является Z = 1.
Для максимального упрощения уравнения необходимо образовывать группы как можно большего размера.
Чтобы закрепить полученные знания, решим следующий пример.
Пример 3——————————————————-
Максимально упростите при помощи карты Карно нормальную форму ИЛИ. Запишите упрощенное уравнение:
X = (AaB)v(AaB)v(AaB).
Сначала полные конъюнкции заносятся в карту (рис. 5.23).
Рис. 5.23. Карта Карно
Затем образуются две группы по два поля. Они имеют значения А и В. Упрощенное уравнение:
X = А а В.
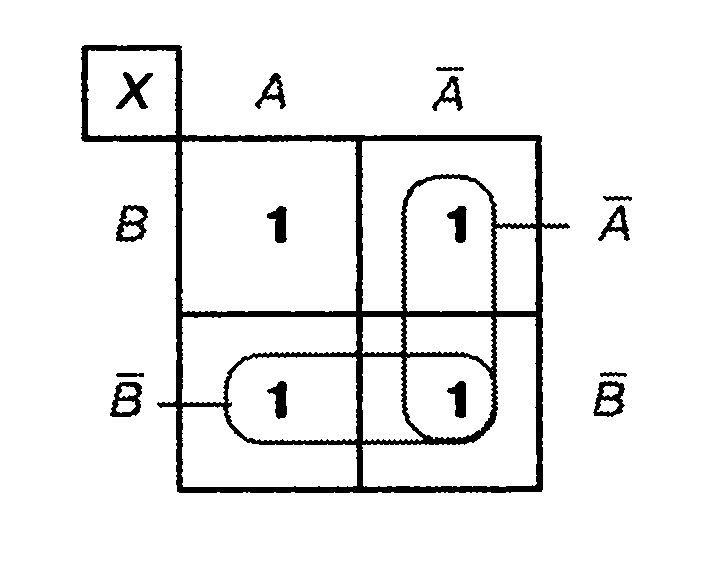
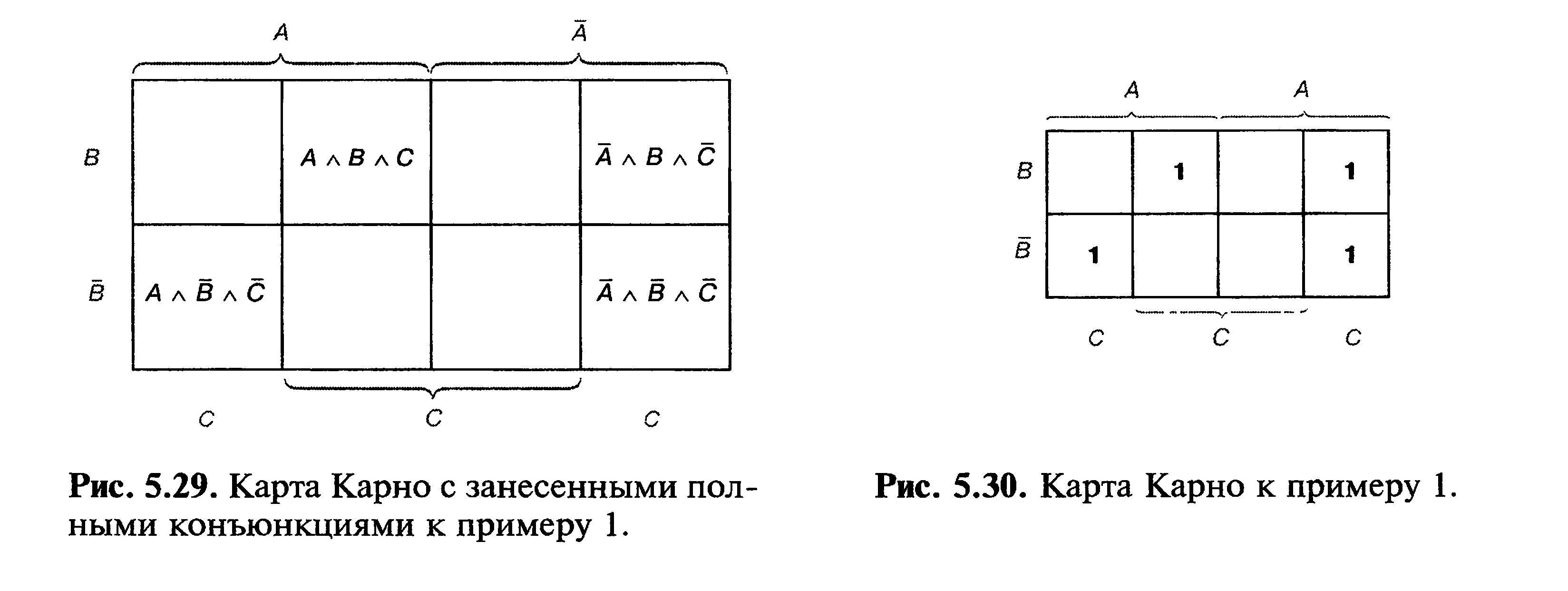
Карта Карно для трех переменных
Для трех переменных возможны 8 различных полных конъюнкций (рис. 5.24). Следовательно, карта Карно для трех переменных должна иметь 8 клеток.
Распределение переменных по координатам может происходить, как и в карте для двух переменных любым образом. Однако целесообразно первые переменные поместить на верхнюю сторону диаграммы, а вторые величины — на левую сторону диаграммы. Третья переменная величина размещается на нижней стороне диаграммы. Для переменных величин А, В и С карта Карно изображена на рис. 5.25.
Третья переменная С должна быть размещена, как указано на рис. 5.25.
Если обозначить обе левые стороны клетки как С, а обе правые как С, то для некоторых полных конъюнкций будет двойное место, а для некоторых — ни одного. На рис. 5.26 полные конъюнкции расписаны по ячейкам.
Для карт Карно с тремя переменными действуют правила, установленные для карт Карно с двумя переменными, со следующими дополнениями:
В одной группе могут быть объединены 2, 4 или 8 соседних полных конъюнкций .
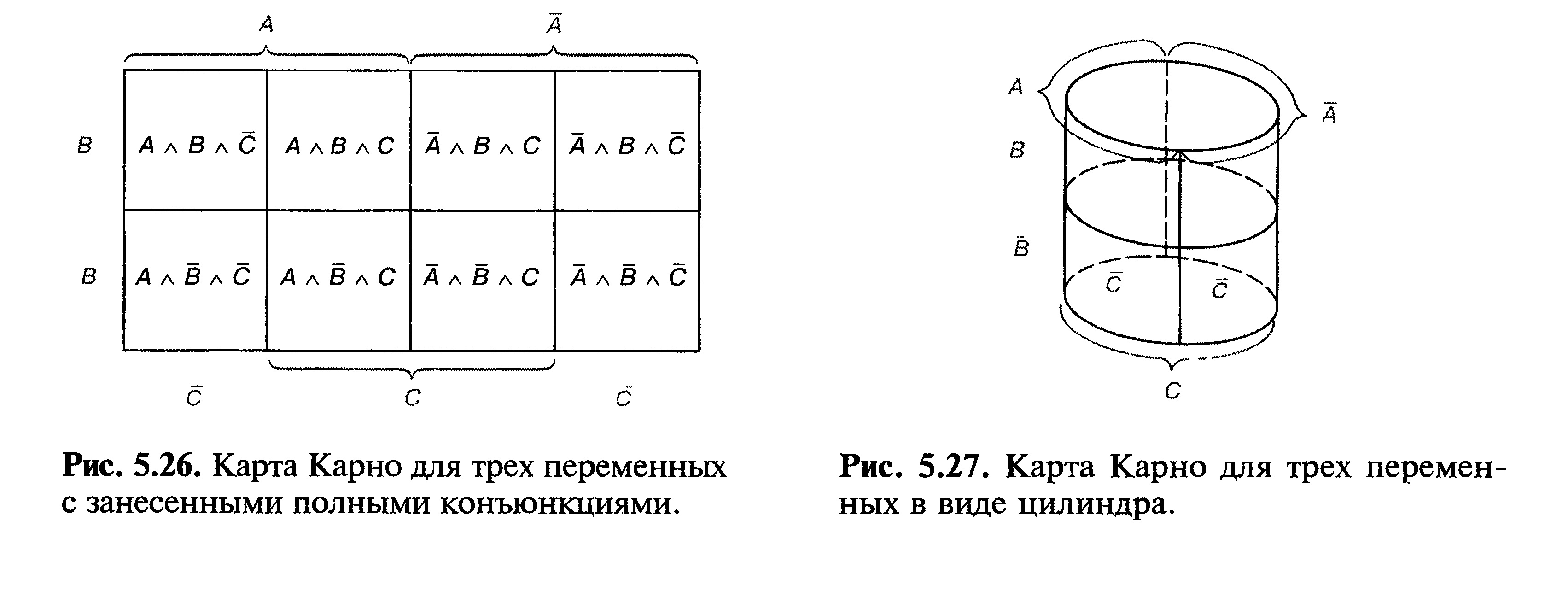
Если быть совсем точными, карта Карно для трех переменных имеет цилиндрическую форму (рис. 5.27). Поэтому клетки, находящиеся в противоположных концах одной строки, являются соседними.
Рис. 5.28. Группировка по принципу расширенного соседства
Карту Карно сложно представлять в виде цилиндра. Поэтому предпочитают форму на рис. 5.25, соблюдая принцип расширенного соседства. На рис. 5.28 представлены соседние полные конъюнкции и их группировки.
Группа из двух клеток на верхней диаграмме имеет в итоге значение В и С.
Группа из четырех клеток на нижней диаграмме имеет значение С. Группа должна быть прямоугольной или квадратной. Группа, изображенная на рис. 5.28а, недопустима.
Рис. 5.28а. Недопустимая группа карты Карно
Рассмотрим несколько примеров работы с картами Карно для трех переменных.
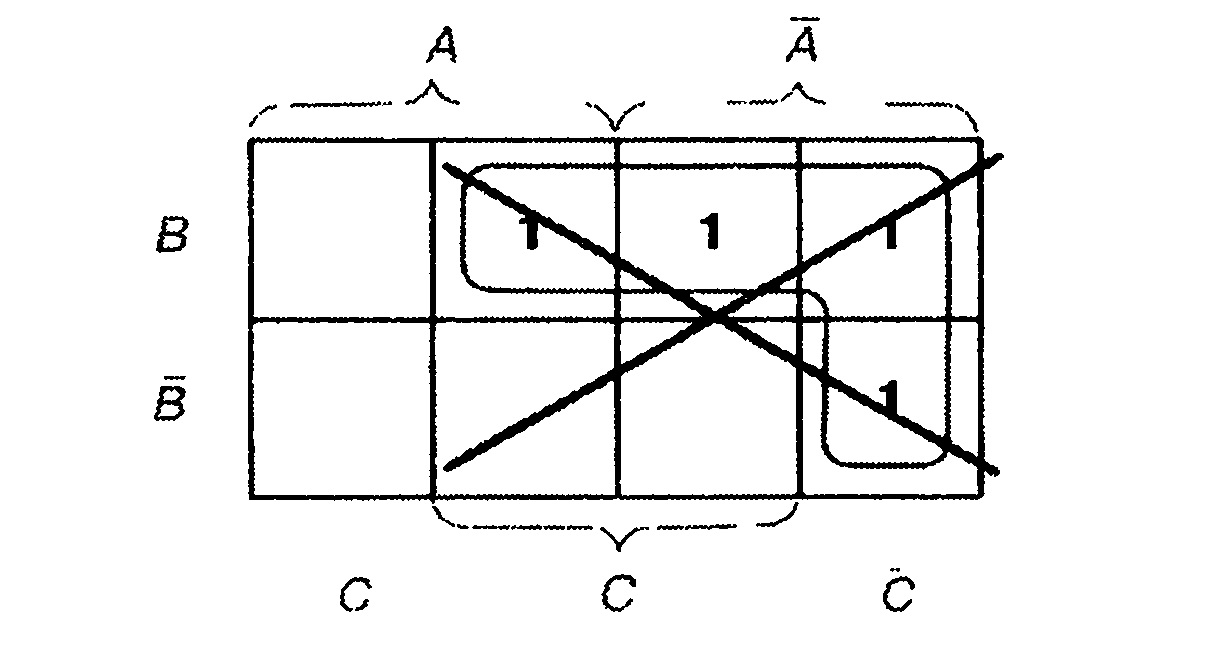
Пример 1——————————————————————-
Заполните карту Карно полными конъюнкциями следующего уравнения:
Y — <^А а В а v а В а v а В а v [А а В а С).
Сначала надо правильно разместить полные конъюнкции по ячейкам (рис. 5.29). Запись лучше производить в алгебраической форме, тогда можно легко контролировать правильность выбора ячейки.
Каждую полную конъюнкцию обозначим 1 (рис. 5.30). При отсутствии затруднений можно сразу же рисовать обычную карту Карно.
Пример 2———————————————————————
Занесите данную нормальную форму ИЛИ в карту Карно и максимально упростите:
Z — (А а В а С) v <А а В л С) v <А а В л С) v а В л С1).
Имеющиеся полные конъюнкции обозначаются 1 (рис. 5.31). Затем производится группировка. Группу из четырех элементов образовать невозможно. Зато можно образовать 3 группы из двух клеток. Однако выделенная пунктиром группа является избыточной, так как двумя основными серыми группами все 1 уже охвачены. Если бы мы выбрали пунктирную группу в качестве основной, найденное уравнение не было бы максимально простым.
Рис. 5.31. Карта Карно к примеру 2
Верхняя серая группа (рис. 5.31) имеет значение А а В. Значение нижней серой группы — В а С. (Переменная А выпадает, так как встречается в координатах этой группы как в прямой, так и в инверсной формах.) Значения групп логически складываются. При этом получается упрощенное уравнение:
Z = (AaB)v(B аС).
Пример 3————————————————————-
Запишите нормальную форму ИЛИ, заключенную в карте Карно (рис. 5.32).
Рис. 5.32. Карта Карно к примеру 3
Максимально упростите нормальную форму ИЛИ.
Нормальная форма ИЛИ по карте Карно:
Z = [А аВ aC^v (А а В aC)v <А аВ aC^v v (А аВ aC^v А аВ аС.
Могут быть образованы 2 группы из четырех клеток. Одна имеет значение В, другая С. Упрощенное уравнение:
Z = BvC.
Так как возможно образование двух больших групп из четырех клеток, то получается значительное упрощение нормальной формы.
Карта Карно для четырех переменных
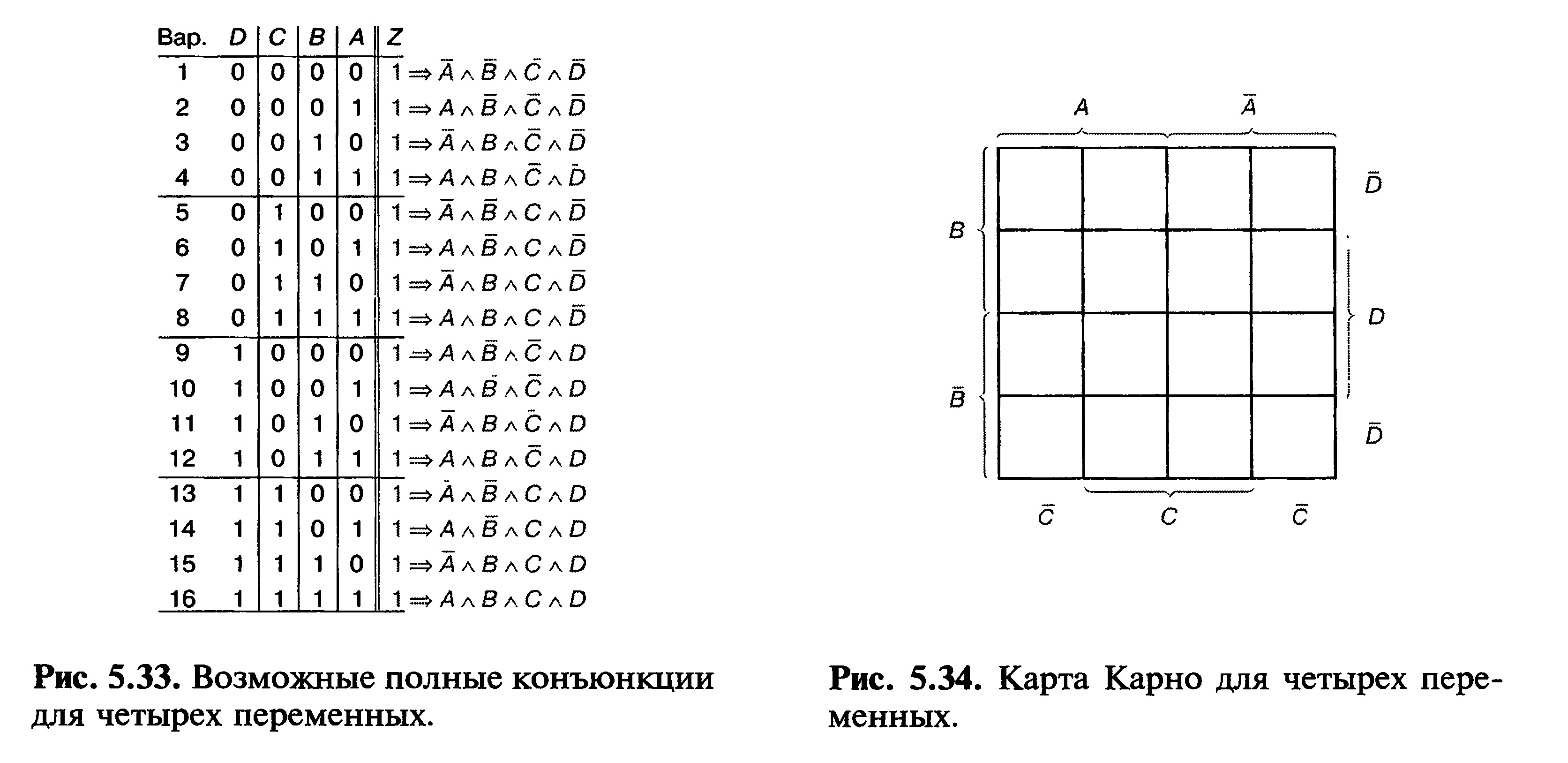
Карта Карно для четырех переменных должна иметь 16 клеток, так как возможны 16 различных полных конъюнкций (рис. 5.33). Карта Карно для четырех переменных изображена на рис. 5.34.
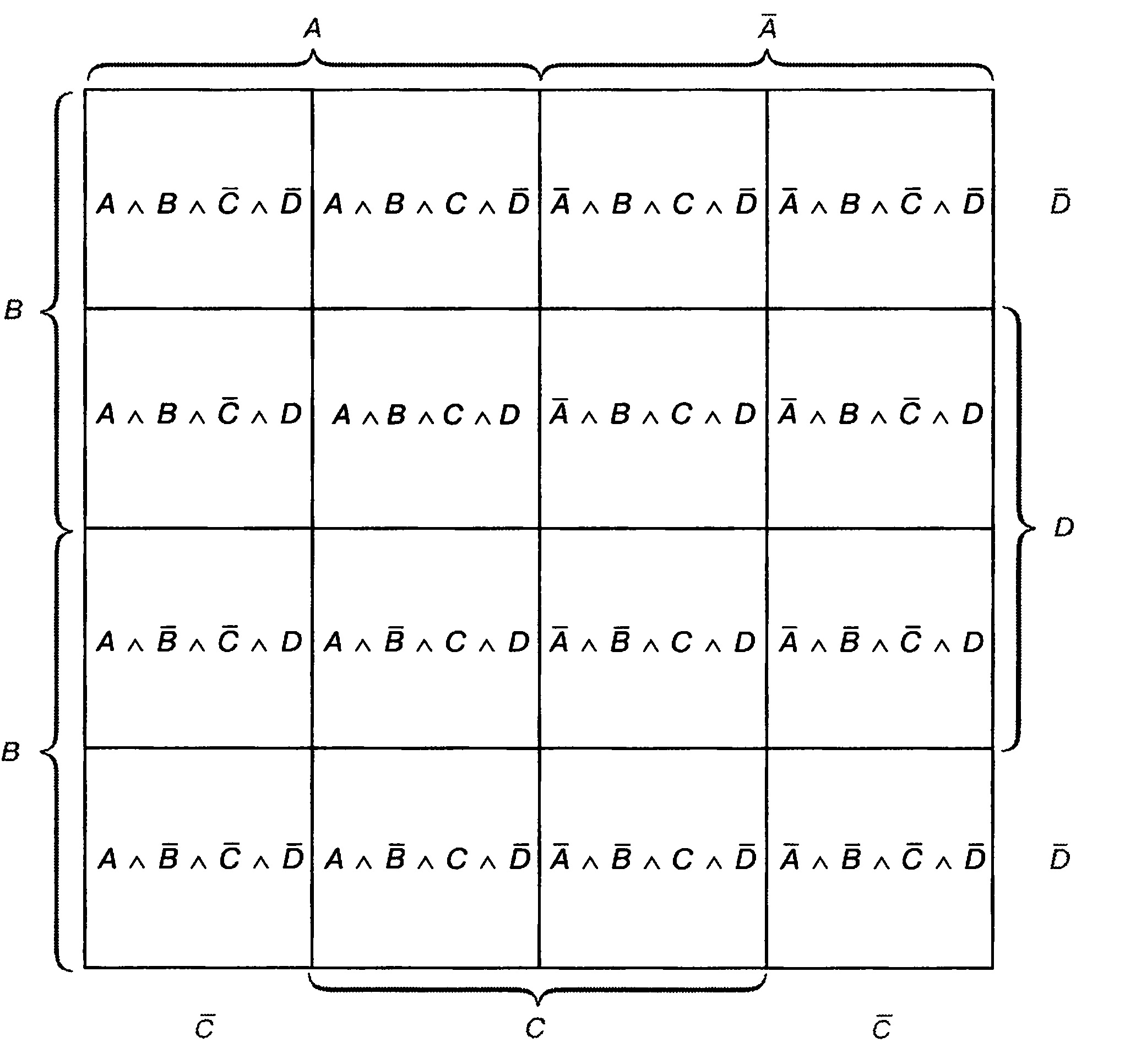
Переменные обозначены, как и раньше, А, В и С. Плюс добавлена переменная величина D. Разумеется, переменные могут быть обозначены иначе, например Ev Е2, Е3, Ег 16 полных конъюнкций показаны на рис. 5.35.
Для карт Карно с четырьмя переменными действуют правила, ранее установленные для карт Карно, со следующими дополнениями:
Рис. 5.35. Карта карно для четырех переменных с занесенными полными конъюнкциями
В одной группе могут быть объединены 2, 4, 8 или 16 соседних полных конъюнкций.
Карта Карно для четырех переменных имеет форму шара. Поэтому клетки, находящиеся в противоположных концах одной строки или столбца, являются соседними.
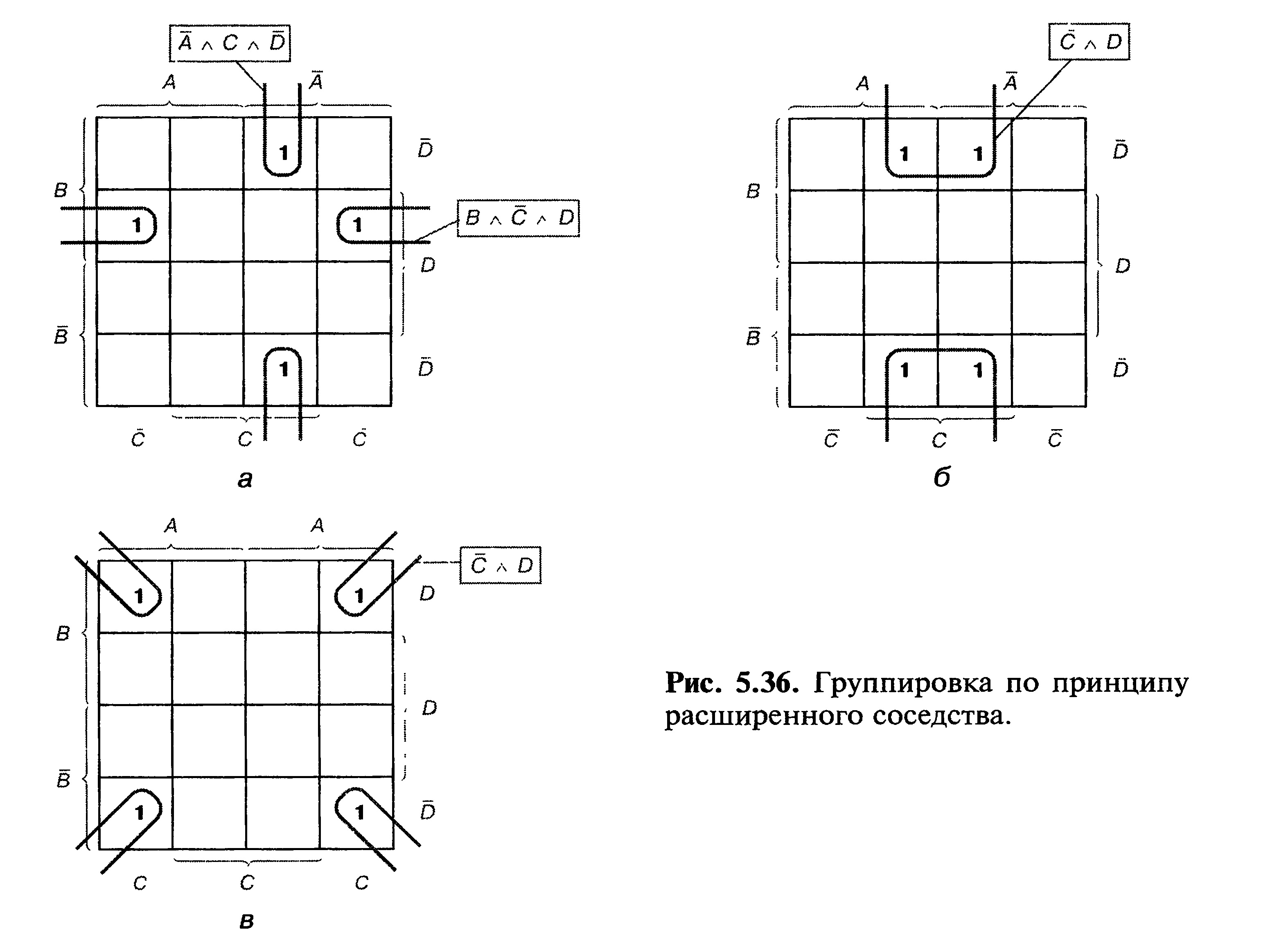
Разъясним подробнее принцип расширенного соседства. Рассмотрим рис. 5.36. Карта (а) показывает, что группы из двух клеток можно образовать не только из полных конъюнкций, которые находятся на концах одной строки, но и из полных конъюнкций, находящихся на концах одного столбца.
Рис. 5.36. Группировка по принципу расширенного соседства
Диаграмма (б) показывает образование группы из четырех клеток.
Диаграмма (в) также показывает образование счетверенной группы. Единицы по У У I К углам являются соседними, так как при
форме шара поля прилегают друг к другу
смежными сторонами.
Другое дело карта на рис. 5.37. Только две единицы по углам не могут образовать сдвоенную группу, так как они не являются смежными — как показано на виде снизу. Рассмотрим ряд примеров с картами Карно для четырех переменных.
Пример 1 ——————————————————
Составьте карту Карно по следующей нормальной форме ИЛИ:
Y = [А л В лС л D^v л В лС л D^v (А л В лС л D)
‘ <А / В аС a (А л В лС л Z)).
Для большей наглядности полные конъюнкции отмечены серыми номерами. Они обозначают соответствующие клетки. На рис. 5.38 показана искомая диаграмма.
Рис. 5.38. Карта Карно к примеру 1
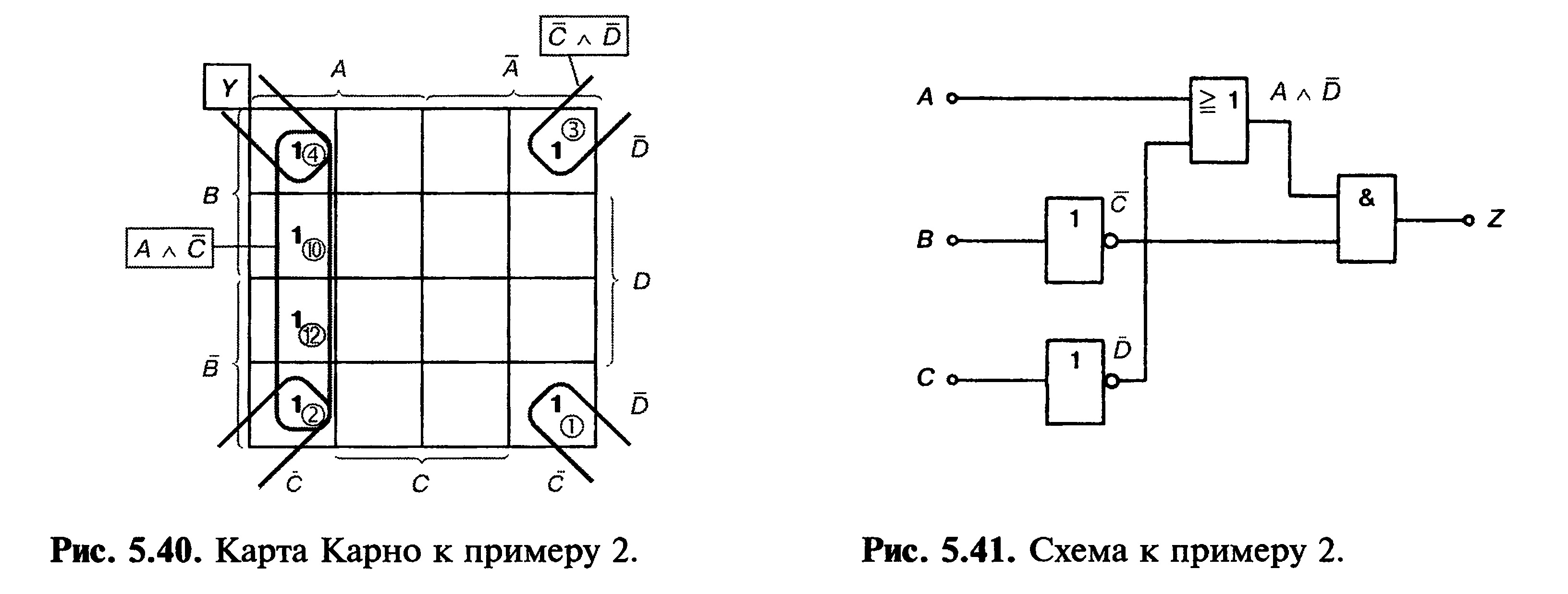
Пример 2—————————————————————-
Для задач управления требуется схема, удовлетворяющая таблице истинности (рис. 5.39). Эта схема должна быть максимально простой.
Рис. 5.39. Таблица истинности к примеру 2
Из таблицы истинности может быть определена нормальная форма ИЛИ Z = [А а В а С a D^jv <А а В а С a D^v [А а В а С a Z))'
v <A А В аС A (А А В аС A (А А В аС A D).
Номера полных конъюнкций совпадают с номерами вариантов таблицы истинности. Полные конъюнкции далее заносятся в диаграмму (рис. 5.40).
Следующим шагом является упрощение нормальной формы ИЛИ с помощью группировки соседних полных конъюнкций. Возможно образование двух групп из 4 клеток со значениями С лВи АлС. Упрощенное уравнение выглядит так:
Z = (с aD)v(AaC).
Переменная С может быть вынесена за скобку:
Z = (С л D)v (А аС) = С а(А v/>).
Получившаяся схема представлена на рис. 5.41.
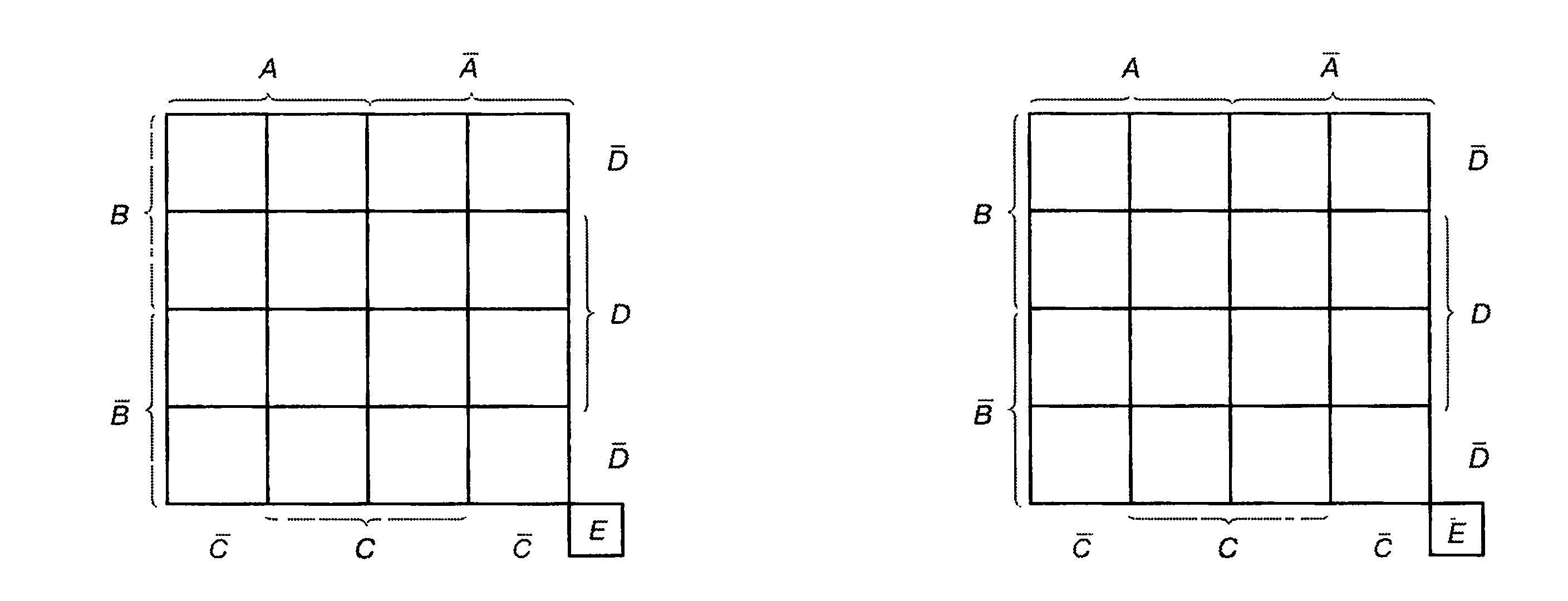
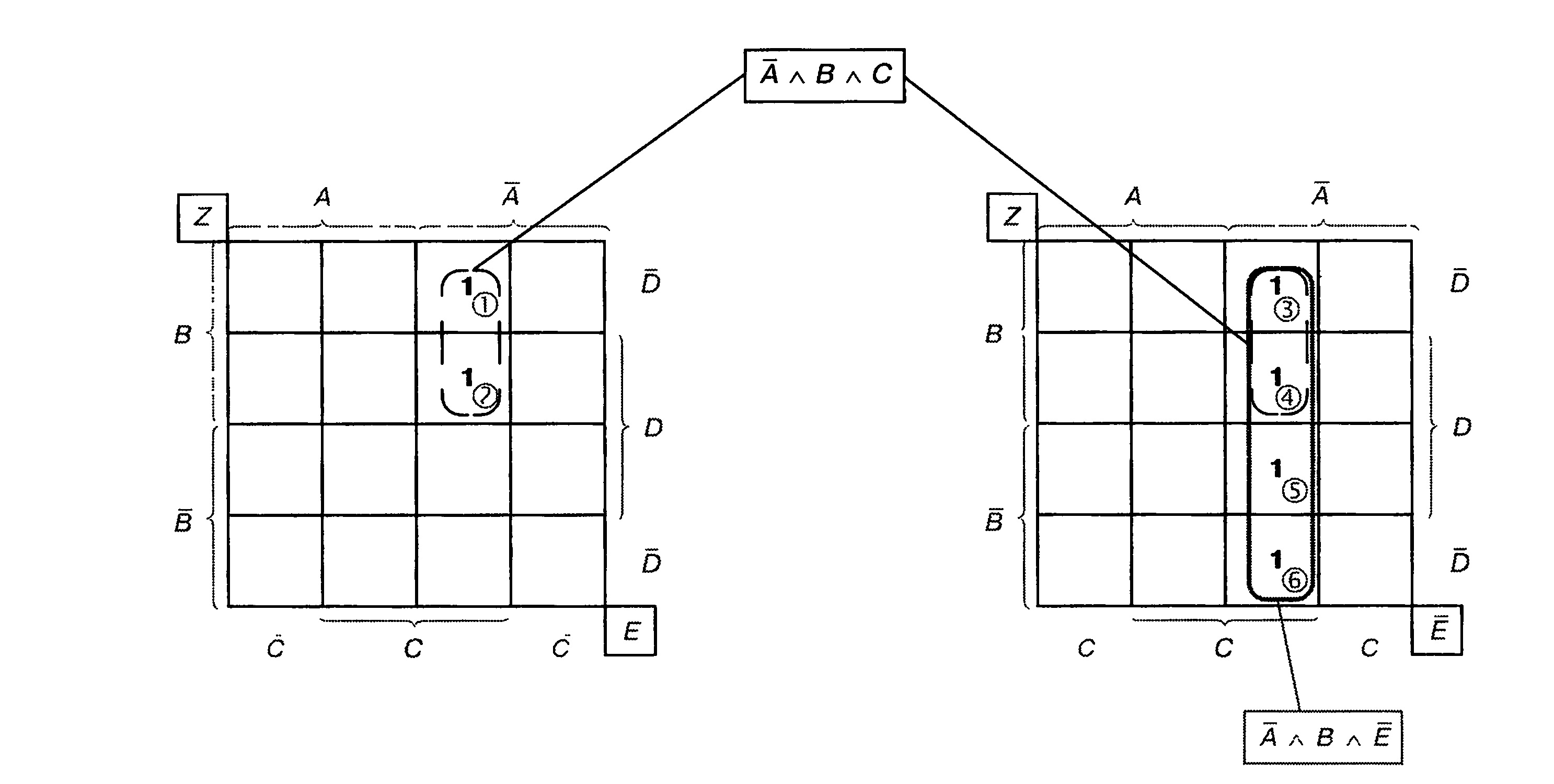
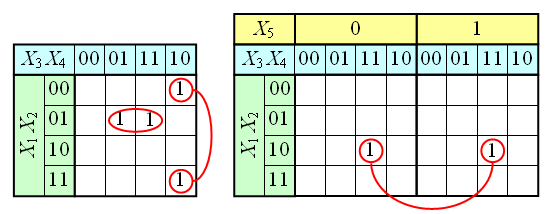
Карта Карно для пяти переменных
Для пяти переменных возможны 32 различные полные конъюнкции. Следовательно, карта Карно для пяти переменных должна иметь 32 поля. Но на одном уровне в диаграмму для четырех переменных новые переменные уже добавить не получится.
Диаграмме надо добавить второй уровень. На рис. 5.42 показано, что имеется в виду. Переменные величины будут, как раньше, обозначены А, В, С и D. К ним добавляется переменная Е.
К нижнему уровню диаграммы присоединяется координата Е, к верхнему — координата Ё. Нарисовать такую двухуровневую карту сложно, поэтому уровни рисуют рядом.
Диаграмма для пяти переменных состоит из двух таблиц, расположенных одна над другой (рис. 5.42а). Такая диаграмма имеет 32 ячейки для 32 полных конъюнкций.
Для карт Карно с пятью переменными действуют правила, ранее установленные для карт Карно, со следующими дополнениями:
Рис. 5.42. Карта Карно для пяти переменных
Рис. 5.42а. Карта Карно для пяти переменных, состоящая из двух таблиц
В одной группе могут быть объединены 2, 4, 8, 16 или 32 соседних полных конъюнкций.
Сгруппированы могут быть также те полные конъюнкции, чьи поля находят-ся друг под другом в таблицах (рис. 5.42).
Рассмотрим эти правила на примерах.
Пример 1————————————————————
Занесите данную нормальную форму ИЛИ в карту Карно и максимально упростите:
Для большей наглядности полные конъюнкции отмечены серыми номерами. Они обозначают соответствующие клетки диаграммы. Возможно образование двух групп из 4 клеток. Серая группа на правой таблице имеет значение АлСлЕ. Переменные В и D в этой группе исключаются.
Рис. 5.43. Карта Карно к примеру 1.
Выделенная пунктиром группа из 4 клеток проходит сквозь оба уровня. Для этого следует мысленно положить друг на друга уровни (рис. 5.43).
Значение этой группы АлВ лС. Так как группа проходит сквозь два уровня, переменная Е выпадает. Переменная D также выпадает. В итоге получается упрощенное уравнение:
Z ^ <А а В aC|v [А а С а Еу
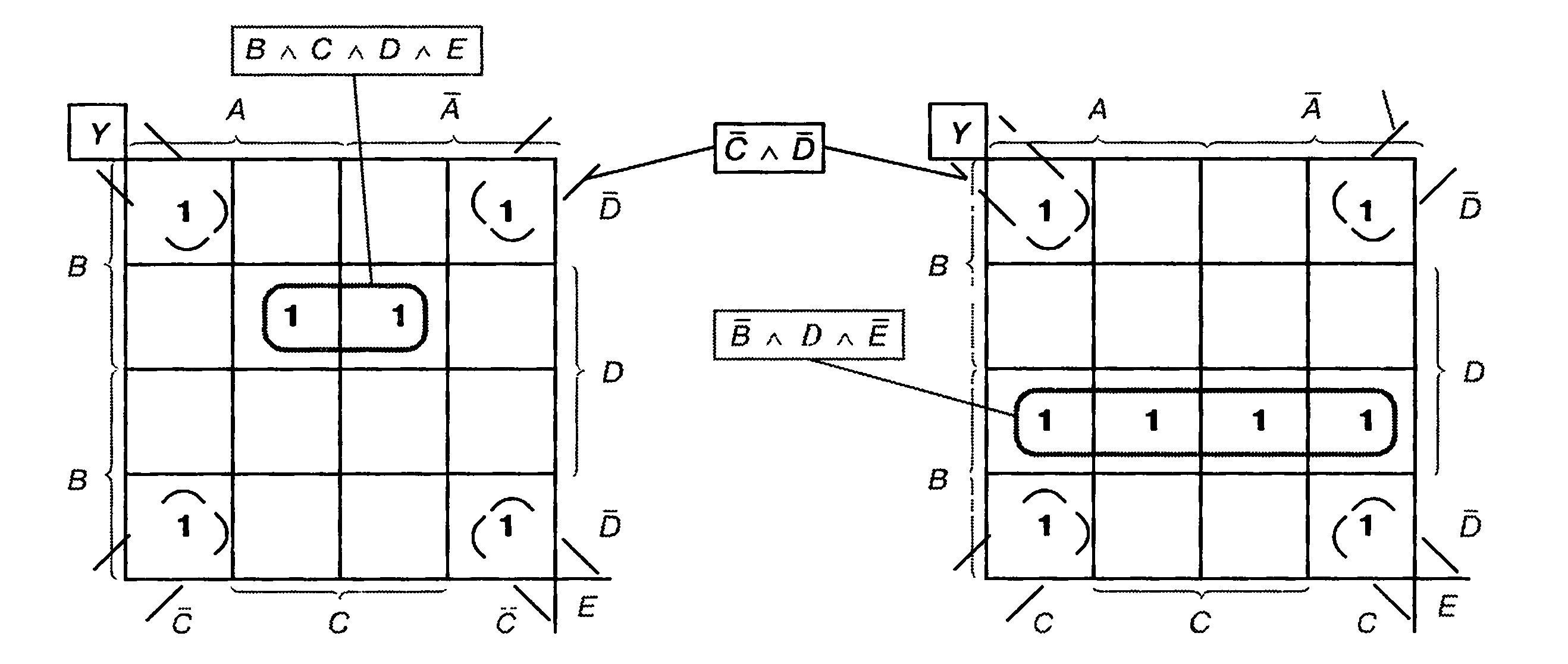
Пример 2————————————————————-
В диаграмме на рис. 5.44 задана нормальная форма ИЛИ. Максимально упростите ее.
Рис. 5.44. Карта Карно к примеру 2
Единицы по углам обоих уровней образуют восьмерную группу (группа
из восьми ячеек). Эта группа проходит через два уровня. Ее значение С л D. Далее можно сформировать группы из 2 и 4 клеток. Группа из 4 клеток
имеет значение В aD л Е. Значение сдвоенной группы В л С л D л Е. Получается упрощенное уравнение:
Y = (CaD)v(BaDaE)v(BaCaDaE).
Упрощение значительно. Это видно, если записать содержащуюся в диаграмме на рис. 5.44 нормальную форму ИЛИ.
Пример 3——————————————————-
Запишите содержащуюся в диаграмме на рис. 5.44 нормальную форму ИЛИ.
Левая таблица диаграммы содержит 6 полных конъюнкций, правая таблица — 8. Таким образом, получается нормальная форма ИЛИ с 14 полными конъюнкциями:
Y = (А А В аС A D A <А А В аС A D A (А А В аС A D A E)v
v(v4 л В аС aD а Е) v (A aBaCaDaE)v (A aBaCaDaE)v
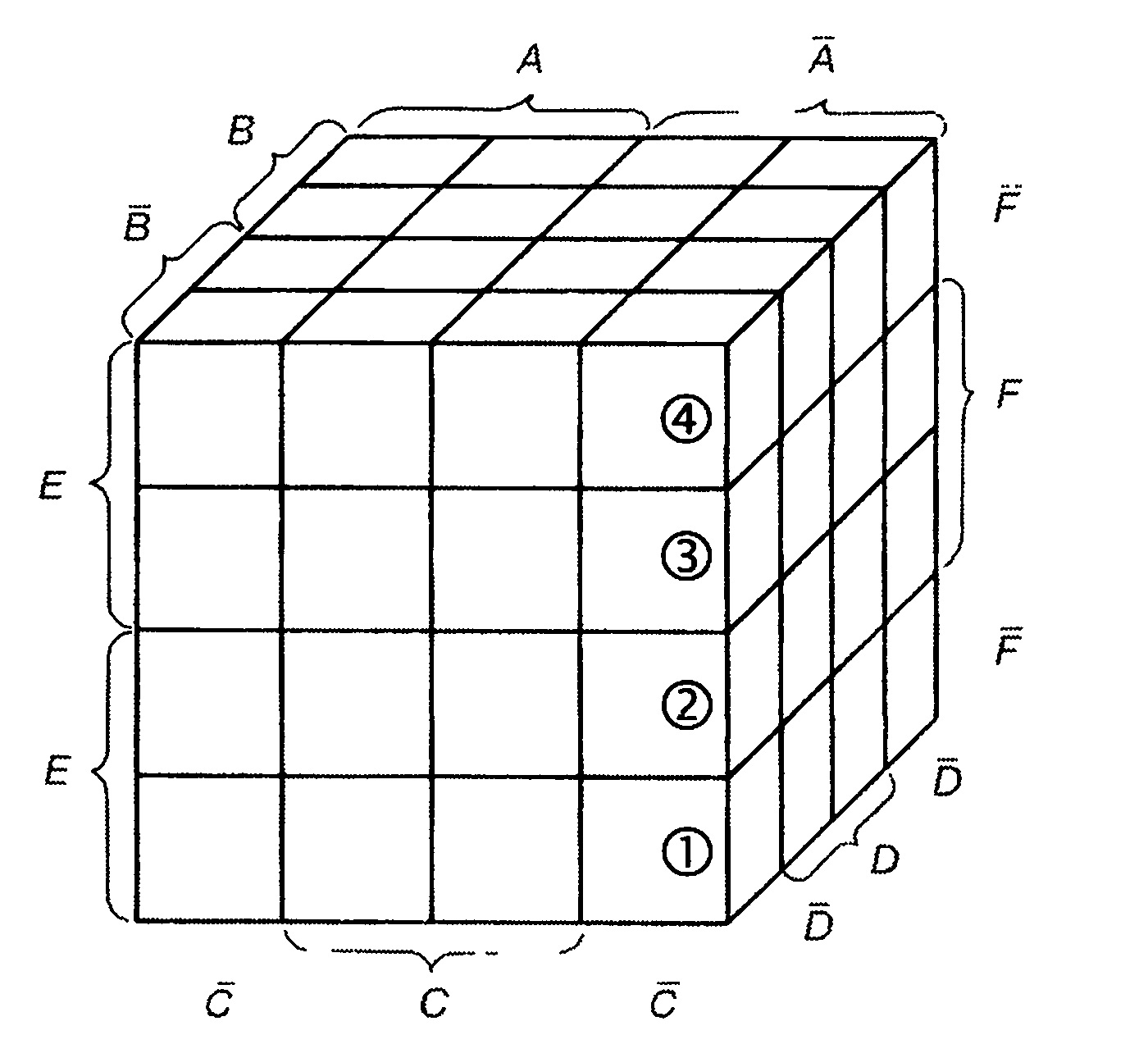
Карта Карно для более чем пяти переменных
На практике нормальные формы ИЛИ с более чем пятью переменными встречаются редко. Поэтому редко возникает необходимость и в диаграммах Карно для более чем пяти переменных. Однако такие диаграммы реальны. Диаграммы для шести переменных еще можно наглядно представить.
При семи и более переменных наглядное представление диаграммы затруднительно.
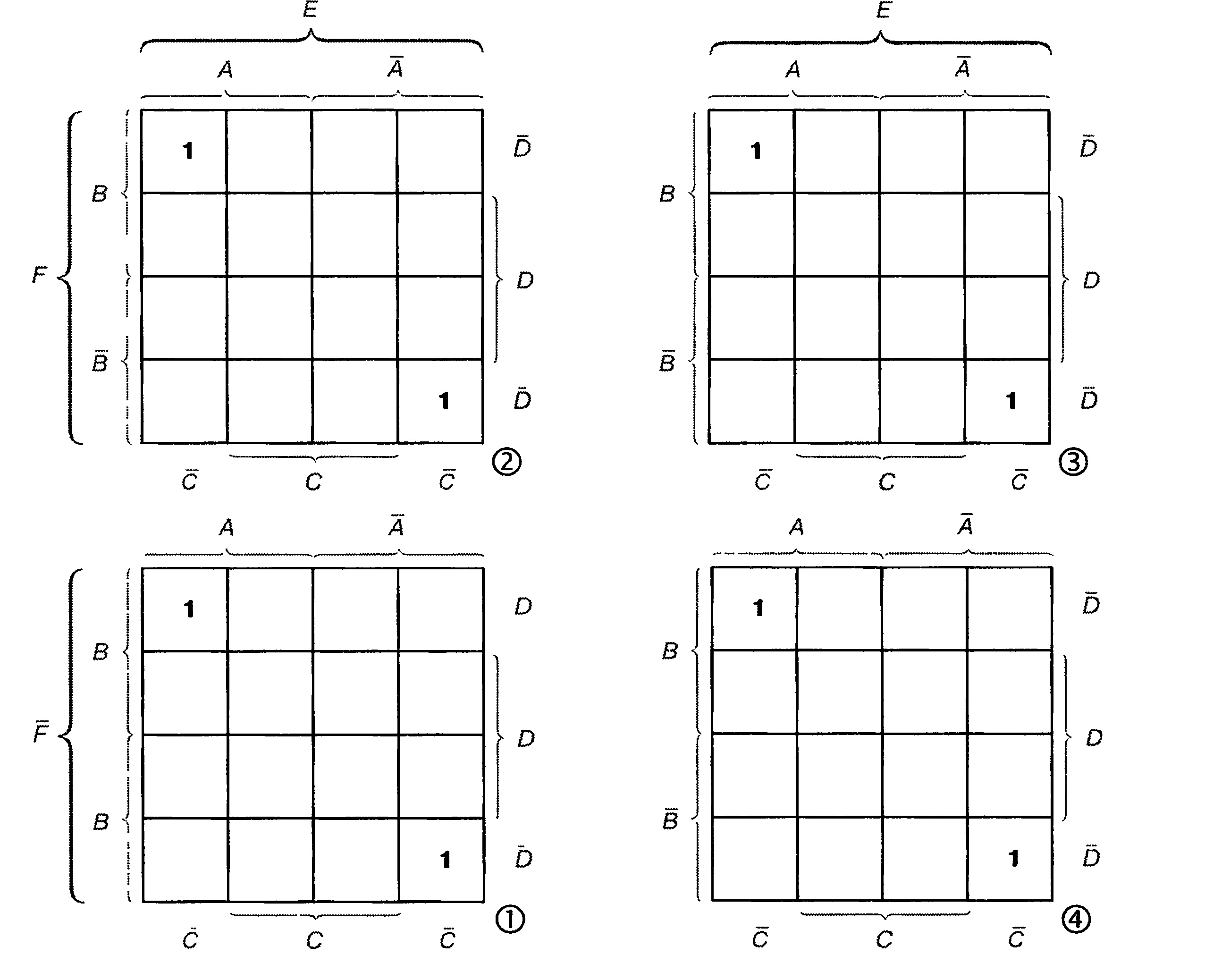
Для шести переменных возможны 64 различные полные конъюнкции. Следовательно, карта Карно для шести переменных должна иметь 64 поля. Если в качестве исходной брать диаграммы ДЛЯ пяти переменных величин, то к ней надо добавить еще третий и четвертый уровни-этажи (рис. 5.45).
Рис. 5.45. Карта Карно для шести переменных
Четыре уровня можно расположить в одной плоскости (рис. 5.46). При группировке нужно постоянно помнить, как реально расположены уровни относительно друг друга.
Рис. 5.45. Карта Карно для шести переменных, развернутая на одной плоскости
Для нормальной формы ИЛИ с шестью и более переменными целесообразно заменять две или три переменных новой переменной. Упрощение может происходить в несколько этапов:
Z = [А а В а С a D л Е л Fjv (л а В а С a D а Е л F’jv v ^А aBaCaDaEa v (A aBaCaDaEa F).
Пример ————————————————————
Все четыре полные конъюнкции содержат переменные А и Е в одинаковом, в данном случае, неинвертируемом виде. Будем рассматривать А а Е как одну переменную.
А а Е = Р.
При таком условии получается нормальная форма ИЛИ только с пятью переменными:
Z = <р А В аС A D A F^<p А В аС A D A F^v
v^PaBaCaDaF^v^PaBaCaDaF).
После упрощения снова заменим Р на А а Е.
💡 Видео
Минимизация логических функций с помощью карт КарноСкачать

Минимизация логических функций. Карты Карно.Скачать

Минимизация логических выражений методом "карты Карно".Скачать

Получение сокращенной ДНФ с помощью минимизирующей карты карты КарноСкачать

A.2.18 Карта КарноСкачать

Минимизация булевых функций. Карты Карно №3Скачать

Лекция 11. Карта КарноСкачать

Диаграмма Карно. Минимизация булевых (логических) функцийСкачать

Карты КарноСкачать

BCD to 7 segment декодер (используя карту Карно)Скачать

Компьютерная логика s01e06: Диаграммы ВейчаСкачать

Карты Карно для функции трёх переменныхСкачать

Метод Диаграмма Вейча / Минимизация логических выражений Veitch Diagram / Подготовка к МЭСКУСкачать

Дискретная математика. Видео 2.2. Метод Карно.Скачать

A.2.15 Построение совершенных дизъюнктивной и конъюнктивной нормальных форм (СДНФ и СКНФ)Скачать

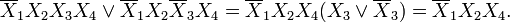

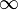 ) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;