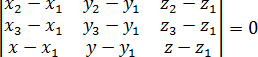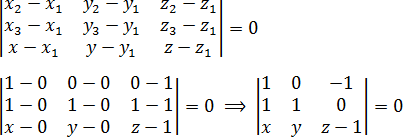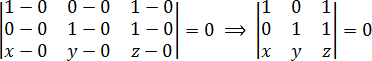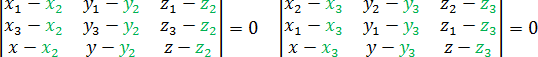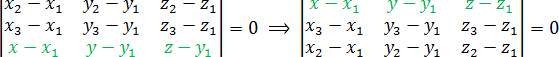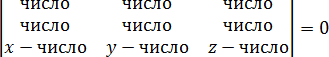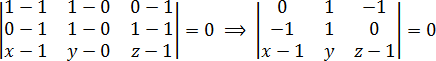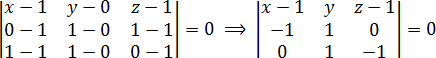Как составить уравнение плоскости пирамиды

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

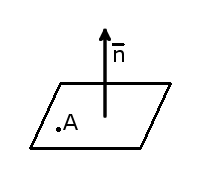
Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Задача C2: уравнение плоскости через определитель

В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Уравнение плоскости по трем точкам

Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:

Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:

Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:

Ax + By + Cz + D = 0

где числа A , B , C и D — коэффициенты, которые, собственно, и требуется найти.

Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Получится система из трех уравнений, которая легко решается.

Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.

Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием обоснований и доказательств.

Видео:Уравнение высоты пирамиды (устар.)Скачать

Уравнение плоскости через определитель

Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.

Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: Тогда уравнение этой плоскости можно записать через определитель:

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:

Задача. Составьте уравнение плоскости, проходящей через точки:

Составляем определитель и приравниваем его к нулю:

a = 1 · 1 · ( z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · ( z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (− x ) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные шли в правильной последовательности. Вот и все! Уравнение плоскости готово!

Задача. Составьте уравнение плоскости, проходящей через точки:

Сразу подставляем координаты точек в определитель:

Снова раскрываем определитель:

a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − ( x + y ) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, рекомендуется — чтобы упростить дальнейшее решение задачи.

Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.

На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит а в какой — Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Откуда берется формула с определителем?

Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.

Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:

Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:

Берем любую точку из первой тройки (например, и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:

Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:

Эта формула означает, что объем параллелепипеда, построенного на векторах равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка как раз то, что мы искали.

Видео:Уравнение плоскости через 3 точкиСкачать

Замена точек и строк определителя

У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:

Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки в самом верху. Пожалуйста, если вам так удобно:

Некоторых смущает, что в одной из строчек присутствуют переменные которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:

Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:

Ax + By + Cz + D = 0

Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.

Задача. Составьте уравнение плоскости, проходящей через точки:

Итак, рассматриваем 4 точки:

Для начала составим стандартный определитель и приравниваем его к нулю:

a = 0 · 1 · ( z − 1) + 1 · 0 · ( x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · ( x − 1) + 1 · (−1) · ( z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z ) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;

Все, мы получили ответ: .

Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными не внизу, а вверху:

Вновь раскрываем полученный определитель:

a = ( x − 1) · 1 · (−1) + ( z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = ( z − 1) · 1 · 0 + y · (−1) · (−1) + ( x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

Мы получили точно такое же уравнение плоскости: Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.

Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.

В рассмотренной выше задаче мы использовали точку но вполне можно было взять В общем, любую точку с известными координатами, лежащую на искомой плоскости.

🔍 Видео

Уравнения стороны треугольника и медианыСкачать

Русские vs американцы. Как решаем мы, а как они | МатематикаСкачать

Уравнение плоскости. 11 класс.Скачать

Математика это не ИсламСкачать

10 класс, 22 урок, Двугранный уголСкачать

Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

Задача про пирамидуСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

2. Уравнение плоскости примеры решения задач #1Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкамСкачать