Как составить уравнение кирхгофа для цепи онлайн (2 видео)

Расчет электрической цепи по закону Кирхгофа

Содержание:

Содержание

Законы Кирхгофа
Порядок составления уравнений но законам Кирхгофа
Пример задачи с решением 3.2.
Расчёт электрических цепей онлайн
Методы расчёта
Расчёт по закону Ома
Расчёт по законам Кирхгофа
Рекомендуемые записи
Как составить уравнение кирхгофа для цепи онлайн
📺 Видео

Законы Кирхгофа

Уравнения, описывающие поведение электрической цепи, составляют на основе законов Кирхгофа. Они определяют связь между токами и напряжениями элементов, образующих цепь. Уравнения, составленные согласно этим законам, называют уравнениями Кирхгофа.

Первый закон Кирхгофа определяет баланс токов в узлах электрической цепи.

Он формулируется следующим образом:

Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

В уравнении (3.1) токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус.

Система уравнений по первому закону Кирхгофа, записанная для всех узлов цепи, линейно зависима. В этом легко убедиться, сложив все уравнения. Поскольку ток каждой ветви входит в два уравнения с разными знаками, сумма тождественно равна нулю. Поэтому число независимых уравнений по первому закону Кирхгофа равно , где — число узлов цепи.

Второй закон Кирхгофа устанавливает баланс напряжений в контуре цепи:

Алгебраическая сумма напряжений ветвей в контуре равна нулю:

Если напряжение ветви совпадает с направлением обхода контура, то напряжению приписывают знак плюс, если же нет — знак минус. Перенесем напряжения источников напряжения, равные ЭДС этих источников, в правую часть. Уравнение (3.2) примет вид

В соответствии с последним равенством алгебраическая сумма напряжений ветвей в контуре электрической цепи равна алгебраической сумме ЭДС источников.

Число независимых уравнений, записанных по второму закону Кирхгофа, равно числу независимых контуров. Число таких контуров определяется формулой , где — число ветвей.

Возможно вам будут полезны данные страницы:

Порядок составления уравнений но законам Кирхгофа

1. Необходимо сначала выбрать положительные направления токов и напряжений ветвей. Положительное направление тока показывают стрелкой на выводе элемента. Положительное направление напряжения показывают стрелкой, расположенной рядом с элементом. Полярности напряжений резисторов выбирают согласованными с направлениями токов. Направления токов источников напряжения выбирают совпадающими с направлениями ЭДС.

2. Записываем уравнения по первому закону Кирхгофа для узлов.

3. Выбираем направления обхода контуров и записываем уравнения по законам Кирхгофа. Сопротивление проводника, соединяющего элементы, очень мало по сравнению с сопротивлением резистора и игнорируется. Ячейки внутренней цепи удобно выбирать в качестве независимых цепей. Можно воспользоваться и другим способом: выбрать по порядку контуры, так, чтобы каждый следующий контур содержал, по меньшей мере, одну ветвь, не входящую в предыдущие контуры.

4. Решаем полученную систему уравнений и определяем токи и напряжения цепи.

5. После определения токов и напряжений необходимо выполнить проверку. Для этого вычисленные значения переменных подставляют в одно из уравнений, составленных по законам Кирхгофа.

При составлении уравнений в качестве неизвестных рассматривают либо токи, либо напряжения резистивных элементов.

В первом случае уравнения цепи составляют относительно неизвестных токов резистивных элементов и напряжений на источниках тока. Напряжения на резистивных элементах, входящие в уравнения по второму закону Кирхгофа, выражают через токи по закону Ома. Такой способ составления уравнений называют токов ветвей.

Число совместно решаемых уравнений в методе токов ветвей можно сократить, если контуры выбирать так, чтобы они не включали источники тока. В этом случае неизвестными будут только токи резистивных элементов, и по второму закону Кирхгофа достаточно составить уравнений, где — количество источников тока.

Во втором случае уравнения цепи составляются относительно напряжений резистивных элементов и токов источников напряжения. Токи резисторов представляют произведением проводимости на напряжение на резисторе. Этот способ составления уравнений называют методом напряжений ветвей.

В дальнейшем для решения задач мы будем использовать в основном метод токов ветвей.

Пример 3.1. Записать уравнения Кирхгофа для цепи, показанной на рис. 3.1.

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. Неизвестными являются токи резистивных элементов . Поэтому необходимо составить пять уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Число уравнений по второму закону Кирхгофа равно двум.

Запишем уравнения по первому закону Кирхгофа для узлов 1, 2, 3. Контуры I и II выберем так, чтобы они не включали источник тока, иначе в системе уравнений появится дополнительная переменная — напряжение источника тока. Направления обхода контуров выберем совпадающими с направлением движения часовой стрелки. В результате получим систему из пяти уравнений с пятью неизвестными токами:

Узел 1: ;

Узел 2: ;

Узел З: ;

Контур I:

Контур II:

Для решения системы уравнений целесообразно использовать математические пакеты, например MathCAD или Matlab.

Напряжение на зажимах источника тока можно затем найти, записав уравнения для контуров, включающих или

Пример задачи с решением 3.2.

Рассчитать токи в цепи, изображенной на рис. 3.2. Номиналы элементов: ,

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. В рассматриваемой схеме шесть неизвестных токов , следовательно, необходимо составить шесть независимых уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Еще три уравнения составим по второму закону Кирхгофа. Наличие источника тока учитывалось при определении числа уравнений по второму закону Кирхгофа.

Составим уравнения по первому закону Кирхгофа для узлов 1, 2 и 3. Уравнения по второму закону Кирхгофа запишем для контуров I, II, III. Направление обхода контуров выбираем по часовой стрелке.

В результате получим систему из шести уравнений с шестью неизвестными токами:

В матричной форме записи:

Решением системы уравнений являются следующие значения токов:

Знак минус в численных значениях токов означает, что направление токов при заданных условиях выбрано навстречу истинному.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Расчёт электрических цепей онлайн

На сайте появилась программа для расчёта установившихся режимов электрических цепей по законам ТОЭ. На настоящий момент реализованы методы расчёта по законам Ома, по законам Кирхгофа, по методу узловых потенциалов, методу контурных токов, методу эквивалентного генератора. Также программа позволяет рассчитать эквивалентное сопротивление цепи относительно источника питания. Программа позволяет нарисовать схему, задать параметры её элементов и рассчитать схему. В результате формируется текстовое описание порядка расчёта, рассчитывается баланс мощностей и строятся векторные диаграммы.

Рисование схемы производится путём перетаскивания элементов методом drag-and-drop из боковой панели и последующим соединением выбранных элементов.

В боковой панели доступны следующие элементы с задаваемыми параметрами:

резистор :
- номер элемента;
- сопротивление, Ом;
конденсатор :
- номер элемента;
- сопротивление, Ом;
катушка индуктивности :
- номер элемента;
- сопротивление, Ом;
источник ЭДС :
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °;
источник тока :
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °.

Инструкция по применению программы приведена здесь.

Методы расчёта

После завершения рисования схемы при нажатии кнопки «Расчёт» запускается расчёт электрической цепи. Программа анализирует исходную схему и при выявлении каких-либо ошибок сообщает об этом. При успешном анализе схемы запускается расчёт по методам ТОЭ.

Расчёт по закону Ома

Расчёт по закону Ома осуществляется для одноконтурных схем. Используемая методика расчёта приведена здесь.

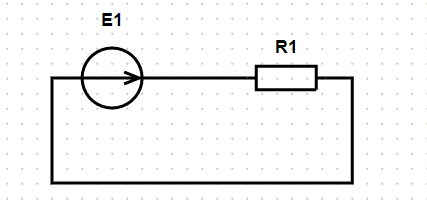
Пример схемы и расчёт:

Исходные данные и схема:

E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
R1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» формируется решение:

В исходной схеме только один контур. Рассчитаем её по закону Ома.

Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ underline $ направление источника ЭДС $ underline_ $:

$$ R_cdot underline = underline_ $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

Отсюда искомый ток в цепи равен

$$ underline = 100space textrm$$

Расчёт по законам Кирхгофа

Для многоконтурных схем расчёт осуществляется по законам Кирхгофа. Используемая методика расчёта приведена здесь.

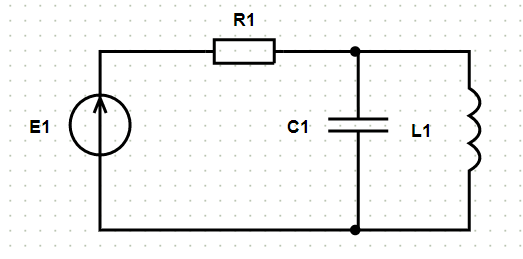
Пример схемы и расчёт:

Исходные данные и схема:

E1:
Номер элемента: 1
Амплитудное значение: 100 В
Начальная фаза: 0
R1:
Номер элемента: 1
Сопротивление, Ом: 1
L1:
Номер элемента: 1
Сопротивление, Ом: 1
C1:
Номер элемента: 1
Сопротивление, Ом: 1

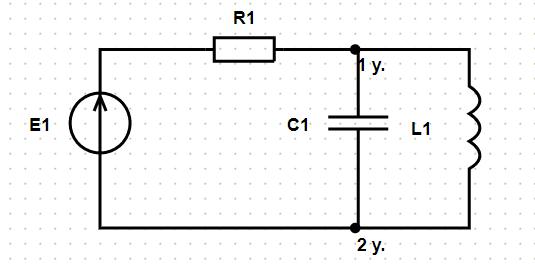
После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:

Рассчитаем схему по законам Кирхгофа.

В данной схеме: узлов − 2 , ветвей − 3, независимых контуров − 2.

Произвольно зададим направления токов в ветвях и направления обхода контуров.

Принятые направления токов:
Ток $ underline_ $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ underline_ $, $ R_ $.
Ток $ underline_ $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_ $.
Ток $ underline_ $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_ $.

Принятые направления обхода контуров:
Контур №1 обходится через элементы $ underline_ $, $ R_ $, $ L_ $ в указанном порядке.
Контур №2 обходится через элементы $ L_ $, $ C_ $ в указанном порядке.

Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».

Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_textrm − 1 $, где $ N_textrm $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.

Составим уравнение для узла №1:

$$ underline_ − underline_ − underline_ = 0 $$

Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.

Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_textrm − N_textrm + 1 $, где $ N_textrm $ — число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.

Составим уравнение для контура №1:

$$ R_cdot underline_ + jX_cdot underline_=underline_ $$

Составим уравнение для контура №2:

$$ jX_cdot underline_ − (−jX_)cdot underline_=0 $$

Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:

$$ beginunderline_ − underline_ − underline_ = 0 \ R_cdot underline_+jX_cdot underline_ = underline_ \ jX_cdot underline_−(−jX_)cdot underline_ = 0 \ end $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

$$ beginunderline_ − underline_ − underline_=0 \ underline_+ j cdot underline_=100 \ j cdot underline_+ j cdot underline_=0 \ end $$

Решим систему уравнений и получим искомые токи: