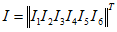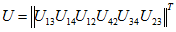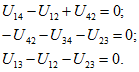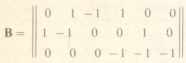Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Трансформаторные подстанции высочайшего качества
Видео:Как составить уравнения по законам Кирхгофа?Скачать
с нами приходит энергия
develop@websor.ru
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать
Законы Кирхгофа в матричной форме
Для записи законов Кирхгофа в матричной форме необходимо составить топологические матрицы схемы.
Матрица соединений , или узловая А ,- это таблица коэффициентов независимых уравнений, составленных по первому закону Кирхгофа для У — 1 узлов. Строки (i) соответствуют узлам (их число равно У- 1), столбцы ( j ) — ветвям (их число равно В). Элемент матрицы aij = + 1, если ветвь j графа соединена с узлом i и направлена от узла i (положительное направление тока в ветви j выбрано от узла i). Элемент матрицы aij = — 1, если ветвь j графа соединена с узлом i и направлена к узлу i . Элемент матрицы aij = 0, если ветвь j не присоединена к узлу i .
Например, для схемы и графа по рис. 1.14 с У= 4 узлами и В = 6 ветвями для первых трех узлов
что соответствует первым трем уравнениям ( 1.21а).
Так как -матрица А определяет, какие ветви присоединены к каждому узлу и как направлены токи в этих ветвях, то произведение матрицы соединений на матрицу-столбец токов ветвей I дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа, и, следовательно, равно нулю:
А I = 0 (1.26а)
— это первый закон Кирхгофа в матричной форме. Для схемы и графа по рис. 1.14
и после выполнения умножения матриц получаем первые три уравнения (1.21а).
Под матрицей соединений иногда понимают матрицу А , записанную для всех узлов схемы.
Матрица сечений Q — это таблица коэффициентов, составленных по первому закону Кирхгофа для сечений. Строки i матрицы соответствуют сечениям (их число равно У — 1), столбцы j — ветвям (их число равно В). Элемент матрицы q ij = +1, если ветвь j содержится в сечении i и направлена согласно с направлением сечения. Элемент матрицы q ij = -1, если ветвь j содержится в сечении i и направлена противоположно направлению сечения. Элемент матрицы q ij = 0, если ветвь j не содержится в сечении i . Для главных сечений составляется матрица главных сечений .
Например, для графа рис. 1.14, д при показанных трех главных сечениях
В матричной форме первый закон Кирхгофа можно записать и с матрицей сечений
После умножения матрицы Q на матрицу-столбец токов I получаются первое и третье (с обратным знаком) уравнения (1.21а) и уравнение (1.216), т. е. независимая система уравнений по первому закону Кирхгофа.
Матрица контуров В — это таблица коэффициентов независимых уравнений, составленных по второму закону Кирхгофа для К = В — (У- 1) независимых контуров. Строки к соответствуют контурам (их число равно К), столбцы j — ветвям (их число равно В).
Элемент матрицы b kj =+1, если ветвь j входит в состав контура k и ее направление совпадает с направлением обхода контура. Элемент матрицы b kj ,= -1, если ветвь j входит в состав контура k и ее направление противоположно направлению обхода контура. Элемент матрицы b kj = 0, если ветвь j не входит в состав контура k .
Матрица В, составленная для главных контуров, приводит непосредственно к независимой системе уравнений по второму закону Кирхгофа. Например, для графа рис. 1.14, д с контурами, состоящими из ветвей 2-4-3 (а), 5-6-4 (б) и 1-6-3 (в) матрица главных контуров при их обходе по направлению движения часовой стрелки
Умножив матрицу В на матрицу-столбец напряжений ветвей, получим матричное уравнение по второму закону Кирхгофа в формулировке (1.20а)
так как каждая строка матрицы В определяет, какие ветви входят в соответствующий контур и с какими знаками должны быть записаны напряжения ветвей.
Для схемы по рис. 1.14, а и ее графа по рис. 1.14, в после умножения на матрицу-столбец напряжений ветвей
получим систему трех независимых уравнений вида (1.20а):
Эта система с учетом равенства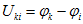 
и соотношений (1.22а) совпадает с ранее полученной системой (1.23), (1.246), (1.24а), т. е. с системой вида (1.206).
Для любой планарной схемы , т. е. схемы, которую можно изобразить на листе без пересекающихся ветвей и проводов, в качестве независимых контуров можно выбирать элементарные контуры-ячейки. Например, для схемы рис. 1.14, а это ячейки I , II , III. Если выбрать направление обхода каждой ячейки по направлению движения стрелки часов, то
После умножения на матрицу-столбец напряжений ветвей U получим другую независимую систему уравнений по второму закону Кирхгофа в форме (1.20 а):
которая после подстановки соотношений (1.22а) приводится к виду (1.206).
Если схема цепи кроме источников ЭДС, как на рис. 1.14, а (и далее рис. 1.20-1.22), содержит и источники тока, то для записи матричных уравнений (1.27) можно рекомендовать преобразование источников тока в источники ЭДС (см. рис. 1.23) или введение понятия обобщенной ветви (см. рис. 1.25).
Видео:Математика без Ху!ни. Метод Гаусса.Скачать
1.6. Первый закон Кирхгофа в матричной форме
Для получения формальной записи первого закона Кирхгофа воспользуемся матрицей инценденций (соединений). Составим эту матрицу.
Пусть задан граф ( рис. 1.10), который содержит 6 ветвей и 4 узла. Матрицу соединений назовем матрицей А . В этой матрице число строк равно числу узлов, а число столбцов равно числу ветвей:
Сформулируем правила заполнения этой матрицы. В месте пересечения строки и столбца ставится +1, если ветвь принадлежит узлу, и ток входит в узел. Если ток выходит из узла, то ставится –1. Если ветвь не принадлежит узлу, то ставится 0.
Как следует из законов Кирхгофа, четвертая строка матрицы А новой информации не несет, поэтому ее можно исключить.
В результате получим редуцированную матрицу А r (с вычеркнутой строкой):
.
Введем матрицу-столбец токов ветвей (разрядность равна количеству ветвей):
Если ввести нуль-матрицу размером, равным числу узлов без одного:
,
то первый закон Кирхгофа может быть записан в матричной форме:
,
или в раскрытом виде:
.
После выполнения действий с матрицами (1.4) получим уравнения, которые соответствуют классическому представлению первого закона Кирхгофа:
Откуда видно, что формула (1.4) составлена правильно.
Видео:Матричный метод решения систем уравненийСкачать
Как составить матрицу из системы уравнений кирхгофа
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где 
— источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:
 . | (1) |
Однако, для дальнейших выкладок будет удобнее представить ток 
как сумму токов k -й ветви и источника тока, т.е.:
 . | (2) |
Подставив (2) в (1), получим:
 . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
 , | (4) |
где Z – диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
 , | (5) |
 , | (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров В , записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c = n — m +1 . Выражение (6) запишем следующим образом:
 . | (7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
 , | (8) |
где 
— столбцовая матрица контурных токов; 
— транспонированная контурная матрица.
С учетом (8) соотношение (7) можно записать, как:
 | (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
 , | (10) |
 . | (11) |
то получим матричную форму записи уравнений, составленных по методу контурных токов:
 , | (12) |
где 
— матрица контурных сопротивлений; 
— матрица контурных ЭДС.
В развернутой форме (12) можно записать, как:
 , | (13) |
то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла ( m =4) и шесть обобщенных ветвей ( n =6). Число независимых контуров, равное числу ветвей связи,
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZB T 
.
Матрицы ЭДС и токов источников
 |  |
 |  |
Тогда матрица контурных ЭДС
.
Матрица контурных токов
 |  . |
Таким образом, окончательно получаем:
,
где 
; 
; 
; 
; 
; 
; 
; 
; 
.
Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
 , | (14) |
где 
— диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.
Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
 , | (15) |
 .. | (16) |
Выражение (16) перепишем, как:
 . | (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А , равным нулю, определим напряжения на зажимах ветвей:
 . | (18) |
Тогда получаем матричное уравнение вида:
 . | (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
 | (20) |
 , | (21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
 | (22) |
где 
— матрица узловых проводимостей; 
— матрица узловых токов.
В развернутом виде соотношение (22) можно записать, как:
 | (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла ( m =3) и 5 ветвей ( n =5) . Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
А 
Диагональная матрица проводимостей ветвей:
Y
где 
.
Матрица узловых проводимостей
.
Матрицы токов и ЭДС источников
 |  |
 |  |
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:
,
где 
; 
; 
; 
; 
.
Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов расчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
🎥 Видео
Лекция по электротехнике 2.5 - Составление уравнений КирхгофаСкачать
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать
Построение матриц электрических цепейСкачать
Решение системы трех уравнений по формулам КрамераСкачать
Решение системы уравнений методом Крамера.Скачать
Решение системы уравнений методом Крамера 2x2Скачать
Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать
Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать
Решение системы уравнений методом обратной матрицы - bezbotvyСкачать
2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать
Решение системы уравнений методом обратной матрицы.Скачать
Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать
Решение матричных уравненийСкачать
решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать
Решение систем линейных алгебраических уравнений методом Крамера.Скачать
