Как составить каноническое уравнение окружности

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение окружности

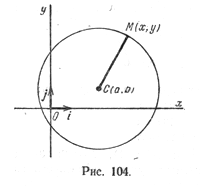
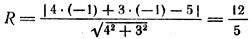Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

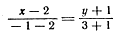
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

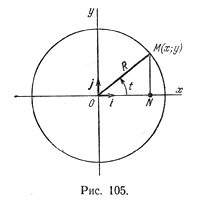
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Видео:Каноническое уравнение окружностиСкачать

ОБЩЕЕ УРАВНЕНИЕ ЛИНИЙ ВТОРОГО ПОРЯДКА

Линии второго порядка

1. Основные понятия.

6. Общее уравнение линий второго порядка.

ОСНОВНЫЕ ПОНЯТИЯ

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

.

Коэффициенты уравнения – действительные числа, но, по крайней мере, одно из чисел отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.

ОКРУЖНОСТЬ

Простейшей кривой второго порядка является окружность.

Определение. Окружностью радиуса R с центром в точке называется множество всех точек плоскости, удовлетворяющих условию .

Каноническое уравнение окружности .

Эллипс

Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.

Каноническое уравнение эллипса .

у

с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.

и называются фокальными радиусами. ,

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

Определение.Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет – величина, определяемая отношением: .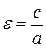

Замечание. Для эллипса .

Определение.Прямые называются директрисами эллипса.

Теорема. Если ­­– расстояние от произвольной точки эллипса до какого-нибудь фокуса, – расстояние от этой же точки до соответствующей этому фокусы директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса: .

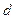
Замечание. Если a = b, то c = 0, а значит, фокусы сливаются, и эллипс превращается в окружность.

Если же 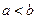, то уравнение определяет эллипс, большая ось которого лежит на оси Оу, а малая ось – на оси Ох. Фокусы такого эллипса находятся в точках F₁ (0;с); F₂(0;-с), где b 2 = a 2 + c 2 .

Пример. Составьте уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), а большая ось равна 2.

Уравнение эллипса имеет вид: .

Расстояние между фокусами: 2c = , таким образом,

a 2 – b 2 = c 2 = .

По условию большая ось равна 2, то есть 2а = 2, откуда получаем, что

а = 1, b = .

Тогда искомое уравнение эллипса имеет вид: .

Гипербола

Определение. Гиперболойназывается линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы .

y

Теорема. Фокусное расстояние и полуоси гиперболы связаны соотношением:

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Прямоугольник со сторонами 2а и2b называется основным прямоугольником гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Замечание.Для гиперболы эксцентриситет .

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/ε от него, называются директрисами гиперболы. Их уравнения: .

Определение. Гипербола называется равносторонней, если ее полуоси равны ( ).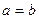

Ее каноническое уравнение .

Определение. Эксцентриситетом гиперболы называется отношение расстояние между фокусами к величине действительной оси гиперболы, обозначается : .

Кривая, определяемая уравнением , также есть гипербола, действительная ось которой расположена на оси , а мнимая ось – на оси .

Гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Пример. Составьте уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса, заданного уравнением

Найдем фокусное расстояние для эллипса:

Тогда искомое уравнение гиперболы .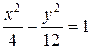

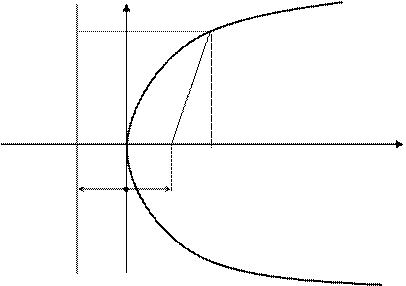
Парабола

Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы y 2 = 2px .

у

Видео:Уравнение окружности (1)Скачать

Конспекты :»Кривые второго порядка»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

1. Окружность и ее уравнение

Кривая второго порядка – линия на плоскости, задаваемая уравнением: Ах 2 +2Вху+Су 2 +2Dx+2Ey+F=0 , где коэффициенты А, В, С, D, E, F – любые действительные числа при условии, что А, В, С одновременно не равны нулю.

Выделяют следующие кривые второго порядка:

Окружностью называется множество точек плоскости, равноудаленных от одной точки, называемой центром.

Пусть центром окружности является точка О ( a;b ), а расстояние до любой точки М ( x;y ) окружности равно R (рис.1). Составим уравнение окружности.

Расстояние от точки М до центра окружности можно найти, пользуясь формулой расстояния между точками:

Подставив в это выражение координаты точек М и О ,получим:

Поскольку расстояние ОМ равно радиусу R , следовательно, R = .

Возведём обе части уравнения в квадрат:

Это уравнение называется каноническим уравнением окружности с центром О ( a ; b ) и радиусом R .

Если центр окружности совпадает с началом координат, то уравнение окружности имеет вид: x 2 + y 2 = R 2 .

Пример 1 Составьте уравнение окружности с центром О (3; -2) и радиусом r = 5.

Решение: Подставив a =3, b =-2 и r = 5 в каноническое уравнение окружности , получим: .

Пример 2 Запишите уравнение окружности с центром в точке М(-3;1), которая проходит через точку К(-1;5)

Подставим значения в уравнение окружности

Составьте уравнение окружности

А. О(-2;1) R =4 Б. М ( 1; -4) , R = 2; В. М ( 0; -5) , R = 3; Г. О (-3;2), R =4.

Составьте уравнение окружности с центром в точке М (1; -4), проходящей через точку А(0; 3).

Определите по уравнению окружности координаты ее центра и радиус :

А) (Х+2)² + ( У – 5)² = 49 Б) (Х+7)² + ( У + 1)² = 36

В) (Х- 6)² + ( У + 15)² = 81 Г) Х ² + ( У -9)² = 2

Эллипс и его уравнение

Эллипсом называется множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами ) есть величина постоянная, большая, чем расстояние между фокусами.

Фокусы эллипса принято обозначат буквами F 1 и F 2 , расстояние между фокусами – через 2с , сумму расстояний от любой точки эллипса до фокусов- через 2а (2а).

Каноническое уравнение эллипса имеет вид:

Где a , b , c – связаннымежду собой равенством или .

Рассмотрим два основных случая расположения эллипса относительно осей координат. Эти случаи представлены в следующей таблице:

Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большей оси. Эксцентриситет обозначается буквой .

Так как по определению 2 a , то эксцентриситет всегда выражается правильной дробью, те 0

Если то эллипс сильно вытянут;

если же то эллипс имеет более круглую форму.

если то эллипс вырождается в окружность.

№ 1Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением

Находим фокусы эллипса: а 2 =16 b 2 =32

Откуда а=4; b =или 4.

Так как b , то фокусы эллипса расположены на оси ординат

Находим длины осей:

Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением:

Гипербола и ее уравнение

Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.

Эта постоянная величина положительна и меньше расстояния меду фокусами.

Фокусы гиперболы принято обозначат буквами F 1 и F 2 , расстояние между фокусами – через 2с , постоянную разность между расстояниями от любой точки гиперболы до ее фокусов — через 2а (2а).

Каноническое уравнение гиперболы имеет вид:

Где a , b , c – связанны между собой равенством .

Рассмотрим два основных случая расположения гиперболы относительно осей координат. Эти случаи представлены в следующей таблице:

Эксцентриситетом гиперболы называется отношение расстояние между фокусами к длине действительной оси.

Так как по определению 2а

Прямые называются асимптотами ; их уравнения имеет вид

№ 1 Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот, если гипербола задана уравнением

Приведем уравнение к каноническому виду, т.е. разделим обе его части на 400

Самостоятельно: Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот, если гипербола задана уравнением .

Парабола и ее уравнение

Параболой называется множество точек на плоскости, равноудаленных от заданной точки ( называемой фокусом ) и данной прямой ( называемой директрисой ).

Фокус параболы принято обозначать буквой F , директрису буквой d , расстояние от фокуса до директрисы — буквой p ( p ). Рассмотрим основные случаи расположения параболы относительно осей координат.

Каноническое уравнение параболы, фокус которой расположен на оси абсцисс (рис.61,62), имеет вид

Эти два случая представлены в следующей таблице:

Каноническое уравнение параболы, фокус которой расположен на оси ординат (рис.63,64), имеет вид

Эти два случая представлены в следующей таблице:

№1 Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением

№ 2 Найти каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0;-3).

Фокус параболы отрицателен, т.к. его координаты (0;-3) следовательно, уравнение параболы имеет вид (ветви параболы направлены вниз ).

Составляем уравнение параболы:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 939 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 587 722 материала в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 17.12.2018
• 254
• 0

• 17.12.2018
• 215
• 0

• 17.12.2018
• 216
• 0

• 17.12.2018
• 882
• 19

• 17.12.2018
• 387
• 6

• 17.12.2018
• 305
• 9

• 17.12.2018
• 686
• 13

• 17.12.2018
• 457
• 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 17.12.2018 5692
• DOCX 162.3 кбайт
• 89 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Фадина Кристина Валерьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 7 месяцев
• Подписчики: 1
• Всего просмотров: 60991
• Всего материалов: 63

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

В Швеции запретят использовать мобильные телефоны на уроках

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только 23 февраля!
Получите новую
специальность
по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

💥 Видео

Написать канонические и параметрические уравнения прямой в пространствеСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Уравнение окружностиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Видеоурок "Гипербола"Скачать

§2 Различные уравнения окружностиСкачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать