Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
Видео:Все графики функций за 20 секундСкачать

1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим (9a) вместо (b):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение (a):
Получается квадратичная функция: (y=-x^2-9x-15).
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).
То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
Видео:Как построить график функции без таблицыСкачать

Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Видео:Квадратичная функция и ее график. 8 класс.Скачать

Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Видео:Занятие 1. График линейной функции y=kx+bСкачать

Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
| x | y |
| 0 | -1 |
| 1 | 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Элементарные функции и их графики
Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.
Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
1. Степенные
К этому типу относятся линейные, квадратичные, кубические, 


2. Показательные
Это функции вида y = a x
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x 2 · e x — произведение квадратичной и показательной функций; y = sin(a x ) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
Графики и свойства основных элементарных функций следует знать наизусть.


n — натуральное, n > 1
n — чётное
n = 2, 4, 6.

n = 3, 5, 7.




| a > 1 |  |
| 0 1 |  |
| 0 2 + 5? Об этом — статья «Преобразования графиков функций». Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций. Почему в уравнении 3 x = 3 5 мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3 x возрастает и каждое значение принимает только один раз. Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически. Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки». 🎦 ВидеоГрафик функции y=x² (y=аx).Скачать  Линейная функция и ее график. 7 класс.Скачать  Как легко составить уравнение параболы из графикаСкачать  Как получить легкий балл на ОГЭ? / Подробный разбор заданий с графиками функций по математикеСкачать  огэ математика сопоставить графики и коэффициенты фукцииСкачать 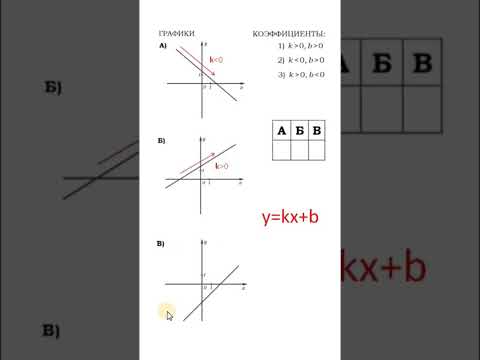 Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать  ОГЭ 2022. Задание 11. Сопоставить функции и графики. Обратная пропорциональность. ГиперболаСкачать  Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать  Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать  Подготовка к ОГЭ №22-графики функции | МатематикаСкачать  Уравнения с модулем. Разбор 22 задания из ОГЭ | Математика 9 класс | TutorOnlineСкачать  Функция у=к/х и её график. Алгебра, 8 классСкачать  |




















 при х ≠ -1.
при х ≠ -1.






 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0. , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
























 , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.
, где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.