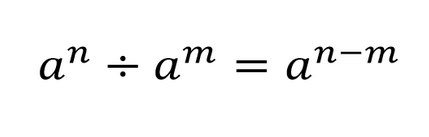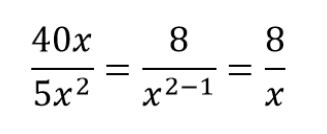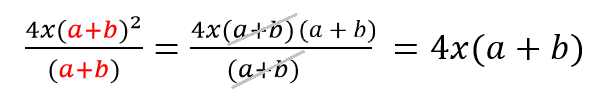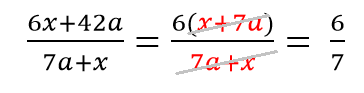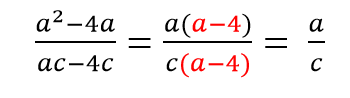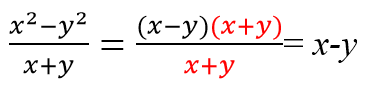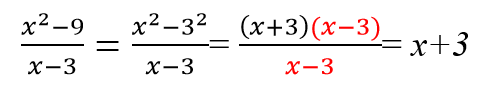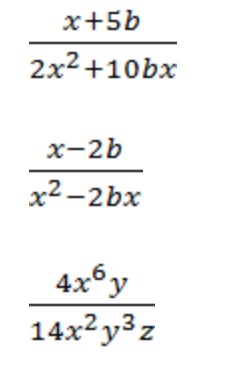- Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
- Квадрат суммы
- Квадрат суммы: ((a+b)^2=a^2+2ab+b^2)
- Квадрат разности
- Квадрат разности: ((a-b)^2=a^2-2ab+b^2)
- Разность квадратов
- Разность квадратов (a^2-b^2=(a+b)(a-b))
- Формулы сокращенного умножения: таблица, примеры использования
- Формулы сокращенного умножения. Таблица
- Дополнительные формулы сокращенного умножения
- Как читать формулы сокращенного умножения?
- Доказательство ФСУ
- Примеры применения ФСУ
- Как сокращать алгебраические дроби?
- Определение
- Сокращение алгебраических дробей
- Сокращение алгебраических дробей с многочленами
- Вынесение общего множителя при сокращении дробей
- Сокращение дробей. Формулы сокращенного умножения
- 📹 Видео
Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
ФСУ используются при упрощении алгебраических выражений (в том числе в работе с алгебраическими дробями ), решении уравнений и неравенств , при разложении на множители и т.д. Ниже мы рассмотрим наиболее популярные формулы и разберем как они получаются.
Видео:Ставим правильно знаки при раскрытии скобок.Скачать

Квадрат суммы
Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: ((a+b)^2). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, ((a+b)^2=(a+b)(a+b)). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь , и привести подобные слагаемые. Получаем:
А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:
Квадрат суммы: ((a+b)^2=a^2+2ab+b^2)
Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.
Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ. Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.
На всякий случай отметим, что в качестве (a) и (b) могут быть любые выражения – принцип остается тем же. Например:
Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду .
Пример. Преобразуйте выражение ((1+5x)^2-12x-1 ) в многочлен стандартного вида.
Раскроем скобки, воспользовавшись формулой квадрата суммы.
…и приведем подобные слагаемые.
Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.
Пример. Вычислите значение выражения ((368)^2+2·368·132+(132)^2) без калькулятора.
Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего. Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: (a^2+2ab+b^2=(a+b)^2)
Вот теперь вычислять гораздо приятнее!
Видео:Раскрытие скобок. 6 класс.Скачать

Квадрат разности
Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для ((a-b)^2):
В более краткой записи имеем:
Квадрат разности: ((a-b)^2=a^2-2ab+b^2)
Применяется она также, как и предыдущая.
Пример. Упростите выражение ((2a-3)^2-4(a^2-a)) и найдите его значение при (a=frac).
Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки .
Теперь приведем подобные слагаемые.
Вот теперь подставляем и наслаждаемся простотой вычислений.
Видео:КАК РАСКРЫТЬ СКОБКИ?Скачать

Разность квадратов
Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:
Разность квадратов (a^2-b^2=(a+b)(a-b))
Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями .
Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус!
Попробуем воспользоваться формулой.
Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
Воспользуемся формулами степеней: ((a^n )^m=a^) и (a^n b^n=(ab)^n).
Ну, а теперь пользуемся формулой (a^2-b^2=(a+b)(a-b)), где (a=5x^2) и (b=m^5 t^3).
Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.
На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем).
Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
Теперь немного преобразуем слагаемые в скобке:
(4xy) запишем как (2·x·2y),
а (4y^2) как ((2y)^2).
Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой (a=x), (b=2y). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как (3) в квадрате.
Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой (a=(x-2y)), (b=3). Раскладываем по ней к произведению двух скобок.
И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
Видео:Как раскрывать скобки.Правило раскрытия скобок.Скачать

Формулы сокращенного умножения: таблица, примеры использования
Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Видео:РАСКРЫТИЕ СКОБОК 7 класс правила раскрытия скобок АЛГЕБРАСкачать

Формулы сокращенного умножения. Таблица
Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения
- формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
- формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
- формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
- формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
- формула разности квадратов: a 2 — b 2 = a — b a + b
- формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
- формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.
Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.
Видео:Видеоурок по теме РАСКРЫТИЕ СКОБОКСкачать

Дополнительные формулы сокращенного умножения
Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.
Во-первых, рассмотрим формулу бинома Ньютона.
a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n
Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:
C n k = n ! k ! · ( n — k ) ! = n ( n — 1 ) ( n — 2 ) . . ( n — ( k — 1 ) ) k !
Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.
Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.
a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n
Как читать эту формулу? Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.
a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1
Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.
Для четных показателей 2m:
a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2
Для нечетных показателей 2m+1:
a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m
Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .
Видео:Уравнения со скобками - 5 класс (примеры)Скачать

Как читать формулы сокращенного умножения?
Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.
a + b 2 = a 2 + 2 a b + b 2 .
Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.
Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:
квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.
Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.
Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.
Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.
Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.
С учетом этого, формулы суммы и разности кубов прочитаются так:
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
Видео:Как быстро раскрывать скобкиСкачать

Доказательство ФСУ
Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.
Для примера рассмотрим формулу квадрата разности.
a — b 2 = a 2 — 2 a b + b 2 .
Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.
a — b 2 = a — b a — b .
a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .
Формула доказана. Остальные ФСУ доказываются аналогично.
Видео:КАК РАСКРЫТЬ СКОБКИ ПРИ УМНОЖЕНИИ, ДЕЛЕНИИ, ВЫЧИТАНИИ? Примеры | МАТЕМАТИКА 5 классСкачать

Примеры применения ФСУ
Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.
Упростим выражение 9 y — ( 1 + 3 y ) 2 .
Применим формулу суммы квадратов и получим:
9 y — ( 1 + 3 y ) 2 = 9 y — ( 1 + 6 y + 9 y 2 ) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2
Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .
Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.
8 x 3 — z 6 4 x 2 — z 4 = 2 x — z ( 4 x 2 + 2 x z + z 4 ) 2 x — z 2 x + z .
Сокращаем и получаем:
8 x 3 — z 6 4 x 2 — z 4 = ( 4 x 2 + 2 x z + z 4 ) 2 x + z
Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.
Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:
79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .
Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.
Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.
Видео:КАК РАСКРЫТЬ СКОБКИ?🙈Скачать

Как сокращать алгебраические дроби?
О чем эта статья:
Видео:6 класс, 39 урок, Раскрытие скобокСкачать

Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Видео:7 класс, 28 урок, Вынесение общего множителя за скобкиСкачать

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Сокращение дробей с буквами и степенями проходит в три этапа:
Определите общий множитель.
Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
Всегда делим на наименьшее значение в степени
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
Общий множитель для числителя и знаменателя — 8.
Х и x 2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
Общий множитель для числителя и знаменателя — 7.
b 3 и b делим на b.
Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Раскрытие скобок - математика 6 классСкачать

Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
сокращайте многочлен в скобках только с таким же многочленом в скобках;
сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
| ❌ Так нельзя | ✅ Так можно |
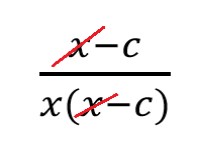 | 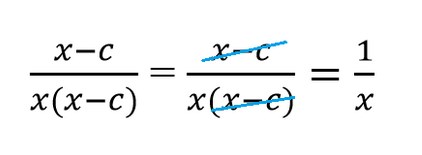 |
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3).
Видео:Правило раскрытия скобок. Сохраняй✅Скачать

Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
Найдите число, на которое делятся числа каждого одночлена.
Найдите повторяющиеся буквенные множители в каждом одночлене.
Вынесите найденные буквенные множители за скобку.
Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
Выносим общий множитель 6
Сокращаем получившиеся одинаковые многочлены.
Пример 2.
Как решаем: в числителе выносим общий множитель a за скобки, в знаменателе выносим общий множитель c за скобки и сокращаем оставшиеся в скобках многочлены.
Видео:Упрощение выражений. 5 класс.Скачать

Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b) 2 = a 2 + 2ab + b 2 |
| Квадрат разности | (a-b) 2 = a 2 — 2ab — b 2 |
| Разность квадратов | a 2 – b 2 = (a – b)(a+b) |
| Куб суммы | (a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 |
| Куб разности | (a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 |
| Сумма кубов | a 3 + b 3 = (a + b)(a 2 — ab+b 2 ) |
| Разность кубов | a 3 — b 3 = (a — b)(a 2 + ab+b 2 ) |
Примеры сокращения дробей с помощью формул сокращенного умножения:
Применяем формулу разности квадратов a 2 − b 2 = (a − b) (a + b) и сокращаем одинаковые многочлены.
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
Поделите числитель и знаменатель на общий множитель.
Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
📹 Видео
Формулы сокращенного умножения | Математика | TutorOnlineСкачать

Сократить дробь алгебра 8 классСкачать

Как решать уравнения с дробью? #shortsСкачать

№2 Квадратное уравнение со скобками (х-1)(x-2)=-6х Как избавиться от скобок в уравнении Как решить уСкачать

КАК РЕШАТЬ ПРОПОРЦИИ?Скачать