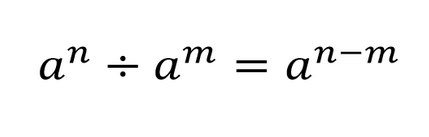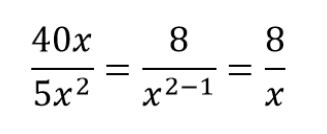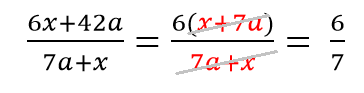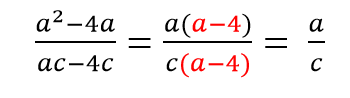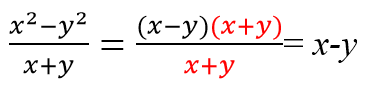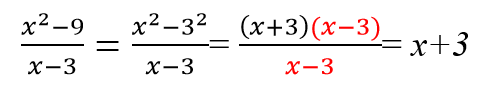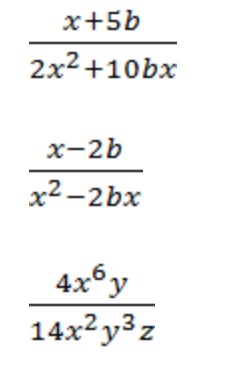О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Определение
- Сокращение алгебраических дробей
- Сокращение алгебраических дробей с многочленами
- Вынесение общего множителя при сокращении дробей
- Сокращение дробей. Формулы сокращенного умножения
- Степенные выражения (выражения со степенями) и их преобразование
- Что представляют собой степенные выражения?
- Основные виды преобразований степенных выражений
- Работа с основанием и показателем степени
- Использование свойств степеней
- Преобразование дробей, содержащих степени
- Преобразование выражений с корнями и степенями
- Преобразование степеней с переменными в показателе
- Преобразование выражений со степенями и логарифмами
- Формулы степеней и корней.
- Формулы степеней.
- 💡 Видео
Видео:СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ | алгебра 7 | ПОКАЗАТЕЛЬ СТЕПЕНИ | свойства степенейСкачать

Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Видео:Сокращаем дроби со степенями №2. Алгебра 8 класс.Скачать

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
- Определите общий множитель.
- Сократите коэффициенты.
- Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
- Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
- Всегда делим на наименьшее значение в степени
- Вычитаем: 3 — 1
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
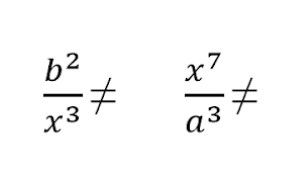 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
- Общий множитель для числителя и знаменателя — 8.
- Х и x 2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
- Общий множитель для числителя и знаменателя — 7.
- b 3 и b делим на b.
- Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:8 класс, 35 урок, Уравнения высших степенейСкачать

Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
- сокращайте многочлен в скобках только с таким же многочленом в скобках;
- сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
| ❌ Так нельзя | ✅ Так можно |
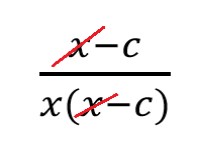 | 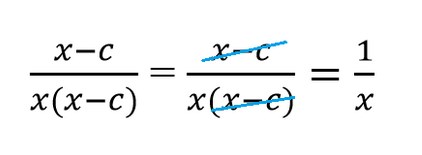 |
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Видео:Алгебра 8. Урок 2 - Сокращение дробейСкачать

Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
- Найдите число, на которое делятся числа каждого одночлена.
- Найдите повторяющиеся буквенные множители в каждом одночлене.
- Вынесите найденные буквенные множители за скобку.
- Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
- Выносим общий множитель 6
- Делим 42/6
- Сокращаем получившиеся одинаковые многочлены.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Видео:Математика| СтепениСкачать

Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b) 2 = a 2 + 2ab + b 2 |
| Квадрат разности | (a-b) 2 = a 2 — 2ab — b 2 |
| Разность квадратов | a 2 – b 2 = (a – b)(a+b) |
| Куб суммы | (a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 |
| Куб разности | (a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 |
| Сумма кубов | a 3 + b 3 = (a + b)(a 2 — ab+b 2 ) |
| Разность кубов | a 3 — b 3 = (a — b)(a 2 + ab+b 2 ) |
Примеры сокращения дробей с помощью формул сокращенного умножения:
Применяем формулу квадрата разности (a-b) 2 = a 2 — 2ab — b 2 и сокращаем одинаковые многочлены.
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
- Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
- Поделите числитель и знаменатель на общий множитель.
- Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
- Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
- Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
- Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
- Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)
Видео:Уравнение четвертой степениСкачать

Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .
Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.
Ответ: 2 3 · ( 4 2 − 12 ) = 32 .
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.
Решение
Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:
9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1
Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .
Видео:Сократить дробь алгебра 8 классСкачать

Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
- a r · a s = a r + s ;
- a r : a s = a r − s ;
- ( a · b ) r = a r · b r ;
- ( a : b ) r = a r : b r ;
- ( a r ) s = a r · s .
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .
Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение
Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .
Решение
Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Ответ: t 3 − t − 6 .
Видео:Степень с натуральным показателем. Свойства степеней. 7 класс.Скачать

Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2
Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3 :
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4
Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 — 1 · x 1 2 + 1
x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .
Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение
Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) — 0 , 2 3 · x — 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .
Видео:8 класс, 6 урок, Степень с целым отрицательным показателемСкачать

Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ: x 1 9 · x · x 3 6 = x 1 3 .
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Видео:Показательные уравнения. 11 класс.Скачать

Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 ( 1 — log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Формулы степеней и корней.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n-ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
5. Возводя степень в степень, показатели степеней перемножают:
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n-ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n-ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m 4 :a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n, нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n, необходимо извлечь корень n–ой степени из m-ой степени этого числа а:
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Формулы степеней.
6. a — n = 
7. 
8. a 1/n = 
💡 Видео
Алгебра 7 класс №1 Контрольная работа В-1 К-4 сократите дробьСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Преобразование выражений, содержащих кв. корни. Сокращение дробей. Практическая часть. 8 класс.Скачать

Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать