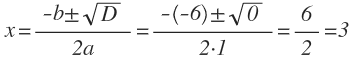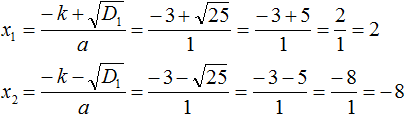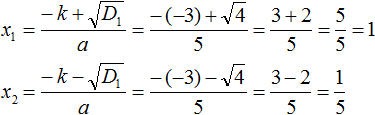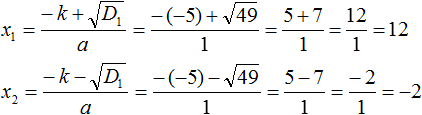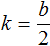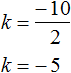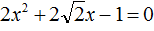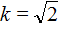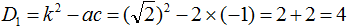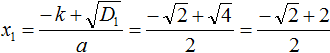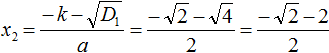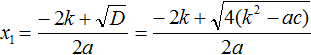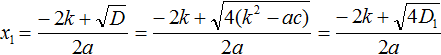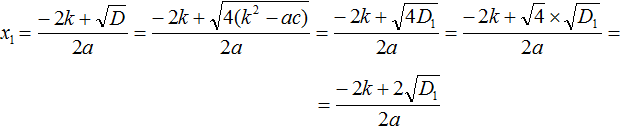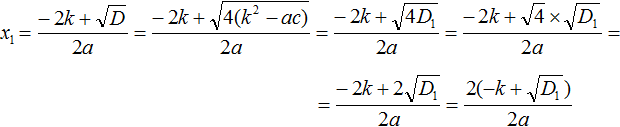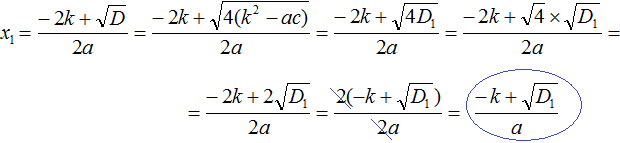Как сокращать уравнение для дискриминанта

О чем эта статья:

Видео:Как решать квадратные уравнения через дискриминант. Простое объяснениеСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:Квадратный трехчлен . Сократить дробь.Скачать

Об отдельных случаях вычисления дискриминанта

Сложно встретить старшеклассника, НЕ умеющего находить корни квадратного уравнения через дискриминант.

Но, к сожалению, в отдельных случаях, получая громоздкий дискриминант, многие начинают паниковать (без калькулятора).

А на ЕГЭ по математике, например, в задачах №11, вам вполне может встретиться причудливый дискриминант.

Нет безвыходных ситуаций!

На чем можно сэкономить силы при вычислении дискриминанта

Прежде чем разбирать примеры, вспомним все же формулу дикриминанта для вычисления корней квадратного уравнения

Тогда корни уравнения находим по формуле

Надеюсь, вы помните, что удобно искать корни уравнения через дискриминант в случае, если имеем дело с полным квадратным уравнением ( и – ненулевые).

I. Используем формулу «разность квадратов» + показать

Допустим, нам нужно решить уравнение

Ясно, что дискриминант следующий:

Не спешим возводить 53 в квадрат! Замечаем, что , поэтому

Корни данного уравнения, думаю, теперь каждый из вас найдет без труда…

II. Используем прием вынесения общего множителя за скобки + показать

Допустим, нам нужно решить уравнение (кстати, оно взято из реальной текстовой задачи из открытого банка заданий ЕГЭ по математике).

Ясно, что дискриминант следующий:

Нет, мы не пойдем напролом!

Замечаем, что , а .

Мы можем вынести за скобку общий множитель

Корни найти – уже не проблема…

III. Формула сокращенного дискриимнанта + показать

Допустим, нам нужно решить уравнение

Вы знаете, что такое ?

Его очень удобно применять в случае четности второго коэффициента (при ).

Вот формулы дискриминанта и корней в этом случае:

для уравнения , где – четное

Тогда корни следующие: , то есть или

Хоть на чуть-чуть, но упростили вычисления. Считаете, что неоправданно, – лишней формулой забивать голову… Выбор за вами.

IV. Вместо дискриминанта – т. Виета + показать

Допустим, нам нужно решить уравнение

Вспоминаем теорему Виета:

Для приведенного квадратного уравнения (т.е. такого, коэффициент при в котором равен единице) сумма корней равна коэффициенту , взятому с обратным знаком, а произведение корней равно свободному члену , то есть ,

Так вот, очевидно, на роль корней уравнения претендуют числа и , так как и

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k 2 − ac , а корни по формулам и .

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Примеры

Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .

Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .

Например, число 10 можно представить как 2 × 5 .

В этом произведении k = 5 .

Число 12 можно представить как 2 × 6 .

В этом произведении k = 6 .

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7 .

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .

В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k 2 − ac

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .

В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D₁ = k 2 − ac не нужно выполнять умножение числа 4 на ac .

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

Пример 5. Решить квадратное уравнение

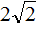
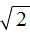
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что

Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .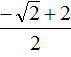

Вычислим второй корень уравнения:

Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k

Теперь вычислим дискриминант по ранее известной формуле:

Вынесем в получившемся выражении за скобки общий множитель 4

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .

В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)

Но ранее было сказано, что выражение k 2 − ac обозначается через D₁ . Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

📹 Видео

ТОП-5 ОШИБОК в математике | Математика | TutorOnlineСкачать

КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать

Как получить легкий балл на ОГЭ? / Подробный разбор заданий с графиками функций по математикеСкачать

Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать

Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Алгебра 8. Урок 2 - Сокращение дробейСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Сократить дробь алгебра 8 классСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать