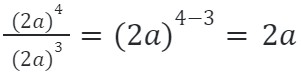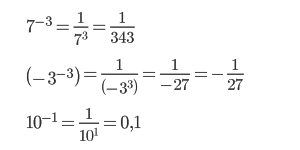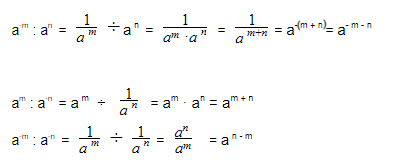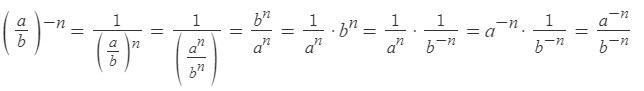- Сложение и вычитание степеней
- Умножение степеней
- Деление степеней
- Примеры решения примеров с дробями, содержащими числа со степенями
- Урок№15. Свойства степени с натуральным показателем. (2 часть)
- Сложение и вычитание степеней
- Сложение степеней с разными показателями
- Сложение степеней с разными основаниями
- Как складывать числа с одинаковыми степенями
- Вычитание степеней с одинаковым основанием
- Вычитание степеней с разными основаниями
- Вычитание степеней с одинаковыми показателями
- Умножение и деление степеней
- Умножение степеней с одинаковыми показателями
- Умножение степеней с одинаковыми основаниями
- Умножение степеней с разными основаниями и показателями
- Деление степеней с одинаковыми основаниями и одинаковыми показателями
- Деление чисел с одинаковыми показателями степени
- Деление степеней с разными основаниями и показателями
- Степень с отрицательным показателем и её свойства
- Умножение отрицательных степеней
- Деление отрицательных степеней
- Возведение дроби в отрицательную степень
- Возведение произведения в отрицательную степень
- Как представить число в виде степени
- Сложение и вычитание степеней
- Что такое степень числа
- Таблица степеней
- Свойства степеней: когда складывать, а когда вычитать
- Свойство 1: произведение степеней
- Свойство 2: частное степеней
- Свойство 3: возведение степени в квадрат
- Свойство 4: степень возведения
- Свойство 5: степень частного
- Сложение и вычитание степеней
- Сложение степеней с разными показателями
- Сложение степеней с разными основаниями
- Как складывать числа с одинаковыми степенями
- Вычитание степеней с одинаковым основанием
- Вычитание степеней с разными основаниями
- Вычитание чисел с одинаковыми степенями
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
| Из | 2a 4 | 3h 2 b 6 | 5(a — h) 6 |
| Вычитаем | -6a 4 | 4h 2 b 6 | 2(a — h) 6 |
| Результат | 8a 4 | -h 2 b 6 | 3(a — h) 6 |
Или:
2a 4 — (-6a 4 ) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
| Первый множитель | x -3 | 3a 6 y 2 | a 2 b 3 y 2 |
| Второй множитель | a m | -2x | a 3 b 2 y |
| Результат | a m x -3 | -6a 6 xy 2 | a 2 b 3 y 2 a 3 b 2 y |
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
| Первый множитель | 4a n | b 2 y 3 | (b + h — y) n |
| Второй множитель | 2a n | b 4 y | (b + h — y) |
| Результат | 8a 2n | b 6 y 4 | (b + h — y) n+1 |
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3 ) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные.
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2 : то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2 )⋅(a 2 + y 2 ) = a 4 — y 4 .
(a 4 — y 4 )⋅(a 4 + y 4 ) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
| Делимое | 9a 3 y 4 | a 2 b + 3a 2 | d⋅(a — h + y) 3 |
| Делитель | -3a 3 | a 2 | (a — h + y) 3 |
| Результат | -3y 4 | b + 3 | d |
Запись a 5 , делённого на a 3 , выглядит как $frac$. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел.
При делении степеней с одинаковым основанием их показатели вычитаются..
Так, y 3 :y 2 = y 3-2 = y 1 . То есть, $frac = y$.
И a n+1 :a = a n+1-1 = a n . То есть $frac = a^n$.
| Делимое | y 2m | 8a n+m | 12(b + y) n |
| Делитель | y m | 4a m | 3(b + y) 3 |
| Результат | y m | 2a n | 4(b +y) n-3 |
Или:
y 2m : y m = y m
8a n+m : 4a m = 2a n
12(b + y) n : 3(b + y) 3 = 4(b +y) n-3
Правило также справедливо и для чисел с отрицательными значениями степеней.
Результат деления a -5 на a -3 , равен a -2 .
Также, $frac : frac = frac.frac = frac = frac$.
h 2 :h -1 = h 2+1 = h 3 или $h^2:frac = h^2.frac = h^3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $frac$ Ответ: $frac$.
2. Уменьшите показатели степеней в $frac$. Ответ: $frac$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Урок№15. Свойства степени с натуральным показателем. (2 часть)
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.
2 3 + 3 4 = 8 + 81= 89
6 3 — 3 3 = 216 — 27 = 189
|
Видео:Математика| СтепениСкачать

Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 2 3 + 2 4 = 8 + 16= 24
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Сложение степеней с разными основаниями
В целом это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые показатели. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 3 4 + 5 4 =81 + 625 = 706
- 1 4 + 7 2 = 1+ 49 = 50
Как складывать числа с одинаковыми степенями
Точно так же, как и в предыдущем примере. Если показатели степени одинаковые, а основания разные — нельзя сложить основания и затем эту сумму возводить в степень.
- 6 3 + 3 3 = 216 + 27 = 243
В уравнениях с этим все проще. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a2.
2,3, 5 — коэффициенты
a 2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Видео:Вспоминаем схему Горнера и уравнения высших степенейСкачать

Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
- 6 3 — 3 3 = 216 — 27 = 189
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые показатели степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 5 4 — 4 4 = 625 — 256 = 369
- 7 4 — 3 2 = 2401 — 9 = 2392
Вычитание степеней с одинаковыми показателями
Все точно так же, как и со сложением. Если показатели степени одинаковые, а основания разные — нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
- 6 3 — 3 3 = 216 — 27 = 189
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a 2 ) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a 2 .
5, 3, 2 — коэффициенты
a 2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Видео:СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ | алгебра 7 | ПОКАЗАТЕЛЬ СТЕПЕНИ | свойства степенейСкачать

Умножение и деление степеней
Здесь всё не так однозначно, как со сложением и вычитанием — общие правила для всех случаев выделить не получится. Все зависит от оснований и показателей степеней, с которыми нужно выполнить манипуляции.
Например, действия со степенями с разными основаниями будут отличаться от действий с числами, у которых основания одинаковые. Работа с показателями — одинаковыми и разными — тоже отличается. Давайте разбираться.
Умножение степеней с одинаковыми показателями
Чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:
- a n · b n = (a · b) n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a 5 · b 5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab) 5
- 3 5 · 4 5 = (3·4) 5 = 12 5 = 248 832
- 16a 2 = 4 2 ·a 2 = (4a) 2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
a m · a n = a m+n , где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 3 5 · 3 2 = 3 5 + 2 = 3 7 = 2 187
- 2 8 · 8 1 = 2 8 · 2 3 = 2 8 + 3 = 2 11 = 2048
Умножение степеней с разными основаниями и показателями
Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 2 8 · 8 1 = 2 8 · 2 3 = 2 11 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
Видео:Сокращаем дроби со степенями №2. Алгебра 8 класс.Скачать

Деление степеней с одинаковыми основаниями и одинаковыми показателями
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми показателями степени
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
- a n : b n = (a : b) n , где
a, b — основание степени, любые числа, b ≠ 0,
n — показатель степени, натуральное число
Пример:
Деление степеней с разными основаниями и показателями
Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:
Видео:Показательные и логарифмические уравнения | Подготовка к ЕГЭ по математике 2024Скачать

Степень с отрицательным показателем и её свойства
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
|
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Видео:КАК РЕШАТЬ УРАВНЕНИЯ СО СТЕПЕНЯМИ? Примеры | АЛГЕБРА 7 классСкачать

Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать  Деление отрицательных степенейПри делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
|
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Видео:8 класс, 35 урок, Уравнения высших степенейСкачать

Как представить число в виде степени
Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.
Например, представим в виде степени число 243:
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Сложение и вычитание степеней
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Умножение и деление степеней. Алгебра, 7 классСкачать

Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
- a n — степень,
a — основание степени
n — показатель степени
Соответственно, a n = a·a·a·a. ·a
Читается такое выражение, как a в степени n.
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то решается она довольно просто:
- 2 3 = 2·2·2, где
2 — основание степени
3 — показатель степени
Действия, конечно, можно выполнять и в онлайн калькуляторе — вот несколько подходящих:
Видео:Уравнения высших степеней. Решение уравнений с помощью деления в столбикСкачать

Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Число
Вторая степень
Третья степень
Видео:Показательные уравнения. 11 класс.Скачать

Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — давайте их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
- a m· a n = a m+n
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
- (a n ) m = a n · m
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
- (a · b) n = a n · b n
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Записывайтесь на курсы обучения математике для школьников с 1 по 11 классы!
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
- (a : b) n = a n : b n
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания. Примеры:
- 2 3 + 3 4 = 8 + 81= 89
- 6 3 — 3 3 = 216 — 27 = 189
Видео:Уравнение четвертой степениСкачать

Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Сложение степеней с разными основаниями
В целом, это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 3 4 + 5 4 =81 + 625 = 706
- 1 4 + 7 2 = 1+ 49 = 50
Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Как складывать числа с одинаковыми степенями
Точно также, как и в предыдущем примере. Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень.
Сначала возводим каждое число в степень и затем выполняем сложение.
- 6 3 +3 3 = 216 + 27 = 243
В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a 2 , например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a 2 .
2, 3, 5 — коэффициенты
a 2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
- 6 3 — 3 3 = 216 — 27 = 189
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 5 4 — 4 4 = 625 — 256 = 369
- 7 4 — 3 2 = 2401 — 9 = 2392
Вычитание чисел с одинаковыми степенями
Все точно также, как и со сложением. Если степени одинаковые, а основания разные, то нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
- 6 3 — 3 3 = 216 — 27 = 189
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a 2 ) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a 2 .
6 и 3 — коэффициенты
a 2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.