Состав растворов обычно выражают в весовых процентах, в молях растворенного вещества на литр раствора (молярность) или на килограмм растворителя (моляльность), а также в мольных долях.
Согласно закону Рауля, давление пара растворителя P1 над раствором пропорционально мольной доле растворителя X1 в растворе:
где 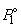
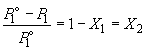
то есть относительное понижение давления пара растворителя над раствором равно мольной доле X2 растворенного вещества.
Если оба компонента раствора летучи, то закон Рауля выполняется для каждого из компонентов:
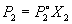
Общее давление пара над раствором равно сумме парциальных давлений P1 и P2:
P = P1 + P2 = 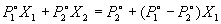
то есть давление пара линейно зависит от состава раствора.
В идеальных растворах закон Рауля выполняется для обоих компонентов во всем интервале составов.
В реальных предельно разбавленных растворах для растворителя выполняется закон Рауля, а для растворенного вещества выполняется закон Генри:
где K2 – константа Генри. В идеальных растворах закон Генри совпадает с законом Рауля (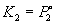
Для описания свойств реальных растворов вводится понятие активности. Активность ai выражается в виде произведения мольной доли Xi компонента на его коэффициент активности
i:
ai = iXi.
Коэффициенты активности растворителя можно рассчитать на основании отклонений от закона Рауля:
i = 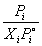
При Xi 1 i 1, то есть ai Xi.
Коэффициенты активности растворенного вещества можно рассчитать на основании отклонений от закона Генри:
i = 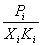
При Xi 0 i 1, то есть ai Xi.
Вклад компонента в любое экстенсивное свойство Z раствора определяется его парциальной мольной величиной. Парциальная мольная величина i-го компонента отражает изменение свойства Z при изменении количества i-го компонента на dni при постоянных P, T и составе в расчете на 1 моль:
Общее значение свойства Z выражается суммой вкладов всех компонентов:
Парциальная мольная энергия Гиббса называется химическим потенциалом :
Парциальные мольные величины компонентов при постоянных P и T связаны уравнением Гиббса-Дюгема:
ПРИМЕРЫ
Пример 7-1. Рассчитать состав раствора бензол – толуол, который при нормальном давлении кипит при температуре 100 o C, а также состав образующегося пара. Раствор считать идеальным. Давления пара чистых бензола и толуола при 100 o C равны 1350 Торр и 556 Торр соответственно.
Решение. Мольную долю бензола в растворе находим по закону Рауля:
Мольная доля толуола в растворе равна X2 = 1 – X1 = 0.743.
Мольная доля бензола в паре равна
Y1 = 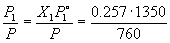
Соответственно, мольная доля толуола в паре равна Y 2 = 1 – Y1 = 0.544.
Пример 7-2. Мольные объемы CCl4 и C6H6 равны 0.09719 и 0.08927 л . моль –1 соответственно, а их парциальные мольные объемы в эквимолярном растворе равны 0.10010 и 0.10640 л . моль –1 . Рассчитать мольный объем эквимолярного раствора и изменение объема при смешении.
Решение. Объем раствора равен
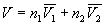
Общий объем до смешения V0 = 0.5 . 0.09719 + 0.5 . 0.08927 = 0.09323 (л . моль –1 ).
Vсмеш. = V – V0 = 0.10325 – 0.09323 = 0.01002 (л . моль –1 ).
ЗАДАЧИ
- Давления пара чистых CHCl3 и CCl4 при 25 o C равны 26.54 и 15.27 кПа. Полагая, что они образуют идеальный раствор, рассчитать давление пара и состав (в мольных долях) пара над раствором, состоящим из 1 моль CHCl3 и 1 моль CCl4.
- Дибромэтилен и дибромпропилен при смешении образуют почти идеальные растворы. При 80 o C давление пара дибромэтилена равно 22.9 кПа, а дибромпропилена 16.9 кПа. Рассчитать состав пара, находящегося в равновесии с раствором, мольная доля дибромэтилена в котором равна 0.75. Рассчитать состав раствора, находящегося в равновесии с паром, мольная доля дибромэтилена в котором равна 0.50.
- Этанол и метанол при смешении образуют почти идеальные растворы. При 20 o C давление пара этанола равно 5.93 кПа, а метанола 11.83 кПа. Рассчитать давление пара раствора, состоящего из 100 г этанола и 100 г метанола, а также состав (в мольных долях) пара над этим раствором при 20 o C.
- Давления пара чистых бензола и толуола при 60 o C равны 51.3 и 18.5 кПа. При каком давлении закипит при 60 o C раствор, состоящий из 1 моля бензола и 2 молей толуола? Каков будет состав пара?
- Давления пара чистых C6H5Cl и C6H5Br при 140 o C равны 1.237 бар и 0.658 бар. Рассчитать состав раствора C6H5Cl – C6H5Br, который при давлении 1 бар кипит при температуре 140 o C, а также состав образующегося пара. Каково будет давление пара над раствором, полученным конденсацией образующегося пара?
- Константа Генри для CO2 в воде при 25 o C равна 1.25 10 6 Торр. Рассчитать растворимость (в единицах моляльности) CO2 в воде при 25 o C, если парциальное давление CO2 над водой равно 0.1 атм.
- Константы Генри для кислорода и азота в воде при 25 o C равны 4.40 10 9 Па и 8.68 10 9 Па соответственно. Рассчитать состав (в %) воздуха, растворенного в воде при 25 o C, если воздух над водой состоит из 80% N2 и 20% O2 по объему, а его давление равно 1 бар.
- Константы Генри для кислорода и азота в воде при 0 o C равны 2.54
10 4 бар и 5.45 10 4 бар соответственно. Рассчитать понижение температуры замерзания воды, вызванное растворением воздуха, состоящего из 80% N2 и 20% O2 по объему при давлении 1.0 бар. Криоскопическая константа воды равна 1.86 К . кг . моль –1 .
- При 25 o C давление пара хлорметана над его раствором в углеводороде при разных мольных долях следующее:
XCH3Cl (р-р) 0.024
PCH3Cl, Торр Показать, что в этом интервале мольных долей раствор подчиняется закону Генри и рассчитать константу Генри.
Содержание- Мольная доля вещества (Ni) в растворе
- Определение мольной доли каждого из веществ раствора
- Коллигативные свойства растворов
- Понижение давления паров
- Первый закон Рауля
- Изотонический коэффициент Вант-Гоффа
- Повышение температуры кипения или понижение температуры затвердевания (кристаллизации). Второй закон Рауля
- Осмотическое давление раствора
- 📸 Видео
Видео:Молярная концентрация. 10 класс.Скачать
Мольная доля вещества (Ni) в растворе
Мольная доля вещества в растворе определяется отношением количества этого вещества к общему количеству вещества в растворе:
,
, (6.6)
где N1 – мольная доля растворенного вещества; N2 – мольная доля растворителя в растворе.
При условии, что раствор состоит из растворителя и одного растворенного вещества, справедливо равенство
Пример 5. Рассчитать мольные доли глюкозы С6H12O6 и воды в растворе с массовой долей глюкозы 36 %.
Решение. Пусть масса раствора m = 100 г. Тогда масса глюкозы в растворе m1 = 36 г, масса воды m2 = 64 г. Определим молярные массы глюкозы и воды:
Определим количество глюкозы и воды в растворе:
Определим мольную долю растворенного вещества – глюкозы:
Определим мольную долю растворителя – воды:
6.1.6. Титр раствора (Т)
Титр раствора определяет массу растворенного вещества в граммах (г), которая содержится в 1 мл раствора. Титр раствора, г/мл, можно рассчитать по уравнению
. (6.8)
Пример 6. Определить титр раствора KOH, эквивалентная концентрация которого Сн = 0,01 н., (моль/л).
Решение. Относительный эквивалент KOH – Э1 = 1. Определим молярную массу KOH:
М1 = (1×39 + 1×16 + 1×1) г/моль = 56 г/моль.
По уравнению (6.8) рассчитаем титр раствора:
Вычисления, связанные с пересчетом концентраций
Растворов из одних единиц в другие
Пример 7. Массовая доля CuSO4 в водном растворе составляет 10 %. Плотность раствора 1,107 г/см 3 . Вычислить молярную, эквивалентную, моляльную концентрацию и мольную долю сульфата меди.
Решение. Молярная масса растворителя (воды) М2 = 18 г/моль. Относительный эквивалент CuSO4 – Э1 = 1/2. Рассчитаем молярную и эквивалентную массу сульфата меди:
М1 = (64 + 32 + 4×16) г/моль = 160 г/моль;
Пусть объем раствора V = 1 л, рассчитаем массу раствора:
m = V×r = 1000 мл × 1,107 г/мл = 1107 г.
Определим массу CuSO4 в одном литре раствора:
Определим массу растворителя (воды) в растворе:
Определим количество растворенного вещества (CuSO4) и растворителя (H2O) в растворе:
Рассчитаем молярную, эквивалентную, моляльную концентрации и мольную долю растворенного вещества:
моль/кг растворителя,
Приготовление разбавленных растворов
Из концентрированных
Разбавлением называется уменьшение концентрации раствора в результате добавления растворителя. Разбавление сопровождается увеличением объема раствора и общей массы раствора. Количество и масса растворенного вещества не изменяются при разбавлении.
Введем обозначения: mx – масса растворителя, добавленного в исходный раствор, г; Vx – объем растворителя, добавленного в исходный раствор, дм 3 ; nx – количество растворителя, добавленного в исходный раствор, моль.
Тогда концентрации разбавленного раствора: С * , С * М, С * н, С * m, N * (1) можно рассчитать на основании следующих уравнений:
; (6.9)
; (6.10)
; (6.11)
; (6.12)
, (6.13)
где С, СМ, Сн, Сm – процентная, молярная, эквивалентная, моляльная концентрации в исходном растворе.
Пример 8. Какой объем раствора ортофосфорной кислоты с массовой долей H3PO4 36 % (r = 1,219 г/см 3 ) требуется для приготовления 13 л 0,15 н. раствора H3PO4?
Решение. Проведем анализ условия задачи и введем обозначения: раствор № 2 получен в результате разбавления раствора № 1. Объем раствора № 2 V * = 13 л, эквивалентная концентрация этого раствора С * н = 0,15 н. Определим количество эквивалентов растворенного вещества и учтем, что при разбавлении количество растворенного вещества в растворе не изменяется. Тогда в соответствии с уравнением (6.11)
где Сн и V – соответственно эквивалентная концентрация и объем раствора № 1. Однако по условию задачи дана массовая доля (С) раствора № 1, поэтому необходимо перейти от массовой доли исходного раствора к его эквивалентной концентрации (см. пример 7): в 100 г исходного раствора содержится 36 г H3PO4 и 64 г H2O; молярная масса и относительный эквивалент H3PO4 соответственно М1 = 98 г/моль; Э1 = 1/3. Рассчитаем эквивалентную концентрацию исходного раствора по уравнению (6.3):
Определим объем раствора 1, который использовали для приготовления 13 л раствора 2:
Видео:ХИМИЯ С НУЛЯ — Как решать задачи по Химии на Массовую ДолюСкачать
Определение мольной доли каждого из веществ раствора
Мольная доля — способ выражения состава раствора, который показывает вклад количества вещества (n, моль) одного из веществ в сумму количеств всех веществ (n, моль) раствора и определяется по соотношению:
где
— сумма количеств (п, моль) всех веществ, входящих в раствор.
Для раствора одного вещества в растворителе эта формула принимает вид:
Рассмотрим примеры решения нескольких задач на тему: «Мольная доля».
Задача 1.
Определите мольную долю каждого из веществ раствора, образованного из 0,7 моль Н2SО4 и 12 моль Н2О.
Дано:
количество вещества серной кислоты: Z(Н2SО4) = 0,7 моль;
количество вещества воды: Z(Н2О) = 12 моль.
Найти:
мольную долю серной кислоты; мольную долю воды.
Решение:
Воспользуемся соотношением для мольной доли.Сумма мольных долей всех веществ раствора равна 100% .
Поэтому мольную долю воды в данном случае можно было определить и путем вычитания.
Часто мольную долго выражают не в процентах, а в долях от единицы. В этом случае в формуле для ее вычисления исчезает умножение на 100%. Значение мольной доли, выраженной в долях от единицы в 100 раз меньше, чем при выражении в процентах. Так, в последней задаче мольная доля серной кислоты, выраженная в долях от единицы, будет:
Мольная доля воды:
Z (Н2О) = 1 – 0,0551 = 0,9449.
Единиц измерения мольная доля не имеет.
Если в условии после значения мольной доли не стоит знака % и само значение меньше единицы, то мольная доля выражена в долях от единицы.
Задача 2.
В некотором количестве воды растворили две соли КС1 и NаС1. Мольная доля воды оказалась равной 0,96, а мольная доля NаС1 в 3 раза большее мольной доли КС1. Определите количества всех веществ (n, моль) в растворе, если известно, что масса растворенного хлорида натрия 5 г.
Дано:
мольная доля воды: Z(Н2О) = 0,96;
отношение мольных долей КС1 и NаС1:
масса хлорида натрия: m(NаС1) = 5 г.
Найти: количество вещества КС1; количество вещества NаС1; количество вещества Н2О.
Решение:
Растворенные соли не взаимодействуют друг с другом, поэтому раствор состоит из трех веществ: КС1; NаС1 и Н2О.Схематично алгоритм решения будет следующим:
1. Определим количество вещества NaCl:
2. Определим количество вещества КС1:
Запишем соотношения для определения мольной доли NаС1 и КС1.
После деления одного выражения на другое, знаменатель во второй части сокращается, и мы получаем:
По условию
а n(NаС1) мы уже определили в первом действии. Это дает нам возможность найти nКС1).
3. Далее определяем количество вещества (п, моль) воды.
Ответ: n(NаС1) = 0,09 моль; n(КС1) = 0,03 моль; n(Н2О) = 3 моль.
Задача 3.
50,0 л газообразного хлороводорода (НС1) (н.у.) растворили в 2 л воды. Определить мольную долю каждого из веществ в полученном растворе.
Дано:
объем газообразного хлороводорода: V(НСl) = 50 л;
объем воды: V(H2О) = 2 л.
Найти:
мольную долю хлороводорода в растворе;
мольную долю воды в растворе.
Решение:
Схематично алгоритм решения можно представить так:Хлороводород при нормальных условиях представляет собой газообразное вещество 1 . Поэтому при (н.у.) к нему применимо следствие из закона Авагадро о молярном объеме газа.
Вода при тех же нормальных условиях является жидкостью. В этом случае неприменим закон Авагадро 2 . Определим массу воды, используя ее плотность (р(Н2О) = 1 г/мл).
m(Н2О) = V . р = 2000 мл . 1 г/мл = 2000 г.
Теперь через молярную массу воды переходим к количеству вещества.
Используя соотношение для мольной доли, вычислим ее для каждого вещества раствора (в долях от единицы).
Ответ: Z(НС1) = 0,02; Z(Н2О) = 0,98.
Итак, при решении задач на определение мольной доли в первую очередь необходимо найти количества вещества (n, моль) всех участников раствора.
Комментарии:
1 В большинстве опытов, которые вы наблюдали в школе на уроках химии, использовалась жидкость с названием «хлороводородная кислота»., или «соляная кислота». На большинстве склянок с этой кислотой просто указывается формула НС1. На самом деле вы видели раствор хлороводорода в воде. Вещество НС1 в чистом виде при обычных условиях представляет собой газ! Названия «хлороводородная кислота» или «соляная кислота» обозначают жидкий раствор НС1 в воде. Если в задачах количество НС1 выражено в объемных единицах (л, мл, м 3 ) и дана ссылка на нормальные условия или конкретные температуру и давление, то речь однозначно идет о газообразном хлороводороде.
2 Применение молярного объема из следствия закона Авогадро для жидкостей является очень грубой и, к сожалению, распространенной ошибкой, свидетельствующей о непонимании материала.Видео:Как ЛЕГКО понять Химию с нуля — Массовая доля вещества // ХимияСкачать
Коллигативные свойства растворов
Любому раствору характерны те или иные физические свойства, к которым относятся и коллигативные свойства растворов. Это такие свойства, на которые не оказывает влияние природа растворенного вещества, а зависят они исключительно от количества частиц этого растворенного вещества.
К коллигативным свойствам растворов относятся:
- Понижение давление паров
- Повышение температуры кипения
- Понижение температуры затвердевания (кристаллизации)
- Осмотическое давление раствора.
Рассмотрим подробнее каждое из перечисленных свойств.
Видео:Способы выражения концентрации растворов. 8 класс.Скачать
Понижение давления паров
Давление насыщенного пара (т.е. пара, который пребывает в состоянии равновесия с жидкостью) над чистым растворителем называется давлением или упругостью насыщенного пара чистого растворителя.
Если в некотором растворителе растворить нелетучее вещество, то равновесное давление паров растворителя при этом понижается, т.к. присутствие какого – либо вещества, растворенного в этом растворителе, затрудняет переход частиц растворителя в паровую фазу.
Экспериментально доказано, что такое понижение давления паров напрямую зависит от количества растворенного вещества. В 1887 г. Ф.М. Рауль описал количественные закономерности коллигативных свойств растворов.
Первый закон Рауля
Первый закон Рауля заключается в следующем:
Давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально мольной доле растворителя в данном растворе:
p — давление пара над раствором, Па;
p0 — давление пара над чистым растворителем, Па;
χр-ль — мольная доля растворителя.
nв-ва и nр-ля – соответственно количество растворенного вещества и растворителя, моль.
Иногда Первому закону Рауля дают другую формулировку:
относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества:
При этом принимаем, что χв-ва + χр-ль= 1
Изотонический коэффициент Вант-Гоффа
Для растворов электролитов данное уравнение приобретает несколько иной вид, в его состав входит изотонический коэффициент i:
Δp — изменение давления паров раствора по сравнению с чистым растворителем;
i – изотонический коэффициент.
Изотонический коэффициент (или фактор Вант-Гоффа) — это параметр, не имеющий размерности, который характеризует поведение какого – либо вещества в растворе.
То есть, изотонический коэффициент показывает, разницу содержания частиц в растворе электролита по сравнению с раствором неэлектролита такой же концентрации. Он тесно связан связан с процессом диссоциации, точнее, со степенью диссоциации и выражается следующим выражением:
n – количество ионов, на которые диссоциирует вещество.
α – степень диссоциации.
Видео:Определение массовых долей элементов в соединениях. 8 класс.Скачать
Повышение температуры кипения или понижение температуры затвердевания (кристаллизации). Второй закон Рауля
Равновесное давление паров жидкости имеет тенденцию к увеличению с ростом температуры, жидкость начинает кипеть, при уравнивании давления ее паров и внешнего давления.
При наличии нелетучего вещества, давление паров раствора снижается, и раствор будет закипать при более высокой температуре, по сравнению с температурой кипения чистого растворителя.
Температура замерзания жидкости также определяется той температурой, при которой давления паров жидкой и твердой фаз уравниваются.
Ф.М. Рауль доказал, что повышение температуры кипения, так же как и понижение температуры замерзания разбавленных растворов нелетучих веществ, прямо пропорционально моляльной концентрации раствора и не зависит от природы растворённого вещества. Это правило известно как Второй закон Рауля:
K — криоскопическая константа,
mв-ва — моляльность вещества в растворе.
Растворы электролитов не подчиняются Законам Рауля. Но для учёта всех несоответствий Вант-Гофф предложил ввести в приведённые уравнения поправку в виде изотонического коэффициента i, учитывающего процесс распада на ионы молекул растворённого вещества:
Видео:ТИПОВЫЕ ЗАДАЧИ ПО ХИМИИ: Химическое Количество Вещества, Моль, Молярная Масса и Молярный ОбъемСкачать
Осмотическое давление раствора
Некоторые материалы имеют способность к полупроницаемости, т.е. им свойственно пропускать частицы определенного вида и не пропускать частицы другого вида.
Перемещение молекул растворителя (но не растворенного, в нем вещества), через полупроницаемую мембрану в раствор с большей концентрацией из более разбавленного представляет собой такое явление как осмос.
Представим два таких раствора, которые разделены полупроницаемой мембраной, как показано на рисунке выше. Растворы стремятся к выравниванию концентраций, поэтому вода будет проникать в раствор, тем самым уменьшая его концентрацию.
Для того, чтобы осмос приостановить, необходимо приложить внешнее давление к раствору. Такое давление, которое требуется приложить, называется осмотическим давлением.
Осмотическое давление и концентрацию раствора неэлектролита позволяет связать уравнение Вант — Гоффа, которое напоминает уравнение идеального газа Клапейрона – Менделеева:
где C — молярная концентрация раствора, моль/м 3 ,
R — универсальная газовая постоянная (8,314 Дж/моль·К);
T — абсолютная температура раствора.
Преобразуем уравнение следующим образом:
C = n/V = m/(M·V)
π = т·R·T / M·V или
Для растворов электролитов осмотическое давление определяется уравнением, в которое входит изотонический коэффициент:
где i — изотонический коэффициент раствора.
Для растворов электролитов i > 1, а для растворов неэлектролитов i = 1.
Если полупроницаемой перегородкой разделены два раствора, имеющие одинаковое осмотическое давление, то перемещение растворителя через перегородку отсутствует. Такие растворы называются изотоническими.
Раствор, с меньшим осмотическим давлением, по сравнению с более концентрированным раствором, называют гипотоническим, а раствор с большей концентрацией – гипертоническим.
📸 Видео
Закон РАУЛЯСкачать
Твёрдый раствор. Закон РауляСкачать
Молярная масса. 8 класс.Скачать
Способы выражения концентрацииСкачать
Как решать задачи с МАССОВОЙ ДОЛЕЙ | Массовая доля растворенного веществаСкачать
задачи на коллигативные свойстваСкачать
Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать
Фазовые равновесия | ФизхимияСкачать
Способы выражения концентрации растворовСкачать
Моляльная концентрация раствора. Решение задач.Скачать
Задача недели. Химия. №43. Законы РауляСкачать
Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать
Составление уравнений химических реакций. 1 часть. 8 класс.Скачать
способы выражения концентрации раствора. Массовая доля. Молярная концентрацияСкачать
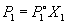
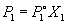
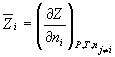
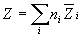
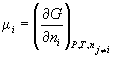
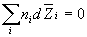
 10 4 бар и 5.45 10 4 бар соответственно. Рассчитать понижение температуры замерзания воды, вызванное растворением воздуха, состоящего из 80% N2 и 20% O2 по объему при давлении 1.0 бар. Криоскопическая константа воды равна 1.86 К . кг . моль –1 .
10 4 бар и 5.45 10 4 бар соответственно. Рассчитать понижение температуры замерзания воды, вызванное растворением воздуха, состоящего из 80% N2 и 20% O2 по объему при давлении 1.0 бар. Криоскопическая константа воды равна 1.86 К . кг . моль –1 .
 ,
, , (6.6)
, (6.6)


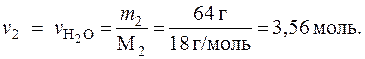


 . (6.8)
. (6.8)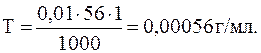
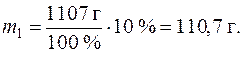



 моль/кг растворителя,
моль/кг растворителя,
 ; (6.9)
; (6.9) ; (6.10)
; (6.10)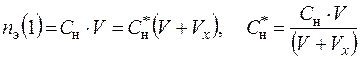 ; (6.11)
; (6.11) ; (6.12)
; (6.12) , (6.13)
, (6.13)



 — сумма количеств (п, моль) всех веществ, входящих в раствор.
— сумма количеств (п, моль) всех веществ, входящих в раствор.