Как решить задачу с уравнением харди вайнберга (4 видео)

Содержание

Расчет частот аллелей в популяции и определение генетической структуры популяции
Расчет частоты аллелей в популяции лисиц
Определение частот генотипов в потомстве группы особей
Как правильно рассчитать структуру популяции по генотипам
Частота встречаемости гомозиготных растений у гречихи
Решение задач по теме «Генетика популяций. Закон Харди-Вайнберга» материал для подготовки к егэ (гиа) по биологии (11 класс) на тему
Скачать:
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Решение задач по теме «Закон Харди-Вайнберга»
Просмотр содержимого документа «Решение задач по теме «Закон Харди-Вайнберга»»
🌟 Видео

Видео:⬆ УЧИМСЯ РЕШАТЬ РАСЧЕТНЫЕ ЗАДАЧИ НА ЗАКОН ХАРДИ-ВАЙНБЕРГАСкачать

Расчет частот аллелей в популяции и определение генетической структуры популяции

Видео:Закон Харди — Вайнберга | НОВАЯ тема ЕГЭ по Биологии | Популяционная генетикаСкачать

Расчет частоты аллелей в популяции лисиц

Задача 380.
Из 14345 лисиц, изученных Ромашовым и Ильиной, 12 лисиц черные, 678 – промежуточной окраски, а 13655 лисиц – рыжие. Найдите частоты аллелей черной и рыжей окраски меха в популяции лисиц. Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга?
Решение:
По условию задачи дается информация об общем количестве фенотипов особей в популяции и по каждому феноипу в отдельности. Промежуточная окраска у лисиц свидетельствует о неполном доминировании рыжей окраски, что указывает на то, что гетерозиготы и являются особями с промежуточной окраской.
Тогда
А — рыжая окраска шерсти;
а — чернафя окраска шерсти;
АА — рыжая лиса;
аа — черная лиса;
Аа — лиса с промежуточной окраской;
Nобщ. = 1445 лисиц;
р 2 (АА) = 1365 лисиц;
2pq(Aa) = 678 лисиц;
q 2 (aa) = 12 лисиц.
Найдем фенотипическую структуру популяции, получим:

p 2 + 2pq + q 2 = 1 = 100%;
р 2 (АА) = 13655/14345 = 0,9519 или 95,19%;
2pq(Aa) = 678/14345 = 0,04726 или 4,726%;
q 2 (aa) = 12/14345 = 0,000836 или 0,0836%.

1. Рассчитаем частоты аллелей черной и рыжей окраски меха в популяции лисиц
По формуле из следствия закона Харди_Вайнберга:

p – частота доминантного аллеля А, q — частота рецессивного аллеля а.

q 2( аа) = 0,000836, q = 0,02898 приблизительно 0,03;
р(А) + q(а) = 1, р(А) = 1 — q(а) = 1 — 0,03 = 0,97.

2. Рассчитаем Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга:

p 2 + 2pq + q 2 = 1 = 100%;
p 2 (АА) + 2pq(Аа) + q 2 (аа) = 1 = 100%;
( 0,97) 2 + 2(0,97 • 0,03 ) + ( 0,03 ) 2 = 1 = 100%;
[0,9519 или 95,19%] + [0,04726 или 4,726%] + [0,000836 или 0,0836%] = 1 = 100%.

Значит, наблюдаемые численности лисиц по фенотипам соответствуют ожидаемым из уравнения Харди-Вайнберга.

Видео:Закон генетического равновесия Харди - Вайнберга. 11 класс.Скачать

Определение частот генотипов в потомстве группы особей

Задача 381.
Определите частоты доминантного и рецессивного аллелей в группе особей, состоящей из 60 гомозигот ВВ и 40 гомозигот bb; в группе, состоящей из 160 особей ВВ и 40 особей bb. Определите частоты генотипов в потомстве этих групп при условии панмиксии.
Решение:
1. Первая группа особей
N_общ. = 60 + 40 = 100
Определим частоты доминантного аллеля, получим:

р 2 (ВВ) = 60/100 = 0,6, значит р = 0,6;
q 2 (bb) = 40/100 = 0,4, значит q = 0,4.

Определите частоты генотипов в потомстве при условии панмиксии, получим:

p 2 + 2pq + q 2 = 1;
p 2 (ВВ) + 2pq(Bb) + q 2 (bb) = 1 = 100%;
(0,6) 2 + 2(0,6 • 9,4) + (0,4) 2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.

р 2 (ВВ) = 0,36 или 36%;
2pq(Bb) = 0,48 или 48%;
q 2 (bb) = 0,16 или 16%.

2. Вторая группа особей
N_общ. = 160 + 40 = 200
Определим частоты доминантного аллеля, получим:

р 2 (ВВ) = 160/200 = 0,8, значит р = 0,8;
q 2 (bb) = 40/200 = 0,2, значит q = 0,2.

Определяем частоты генотипов в потомстве при условии панмиксии, получим:

p 2 + 2pq + q 2 = 1;
p 2 (ВВ) + 2pq(Bb) + q 2 (bb) = 1 = 100%;
(0,8) 2 + 2(0,8 • 0,2) + (0,2) 2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.

р 2 (ВВ) = 0,64 или 64%;
2pq(Bb) = 0,32 или 32%;
q 2 (bb) = 0,04 или 4%.

Как правильно рассчитать структуру популяции по генотипам

Задача 382.
Доля особей, имеющих генотип (аа), в большой естественной популяции равна 0,16. Рассчитайте структуру данной популяции по генотипам.
Решение:
q 2 (aa) = 0,16 = 16%;
p 2 (AA) = ?
2pq(Aa) = ?
Зная частоту встречаемости рецессивных гомозигот (аа), рассчитаем частоту встречаемости рецессивного аллеля (а), получим:

Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту встречаемости аллеля гена (А), получим:

p + q = 1 = 100%, где
р – частота доминантного аллеля в популяции;
q — частота рецессивного аллеля в популяции.

p + q = 1; p(A) + q(a) = 1; p(A) = 1 – q(a);
p(A) = 1 – 0,4 = 0,6.

Используя второе следствие из закона Харди-Вайнберга рассчитаем структуру данной популяции по генотипам, получим:

p 2 + 2pq + q 2 = 1 = 100%, где
p 2 – частота встречаемости доминантных генотипов в популяции;
2pq — частота встречаемости гетерозигот в популяции;
q 2 — частота встречаемости рецессивных генотипов в популяции.

р 2 (АА) + 2pq(Aa) = q 2 (aa) = 1 = 100%;
(0,6) 2 + 2(0,6 • 0,4) + (0,4) 2 = 1 = 100%;
0,36 или 36%(АА) + 0,48 или 48%(Аа) + 0,16 или 16%(аа) = 1 = 100%.

Ответ:
р 2 (АА) = 36%;
q 2 (aa) = 16%;
2pq(Aa) = 48%.

Частота встречаемости гомозиготных растений у гречихи

Задача 383.
У гречихи ярко-красная окраска растений неполно доминирует над зеленой. Гетерозиготы по данным генам имеют розовую краску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?
Решение:
А – ярко-красная окраска растения;
а – зеленая окраска растения;
Аа – розовая окраска растения;
N_общ. = 840 растений;
N(AA) = 42 ярко-красных растения;
р 2 = ?
q 2 = ?
1. Рассчитаем долю (частоту) встречаемости доминантных гомозигот (А) в популяции гречихи из условия задачи, получим:

р 2 (АА) = N(AA)/N_общ. = 42/840 = 0,05 или 5%.

2. Зная частоту встречаемости доминантных гомозигот (АА) в популяции рассчитаем частоту аллели гена (А), получим:

3. Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту рецессивного аллеля (а) в популяции гречихи, получим:

p + q = 1; p(A) + q(a) = 1;
q(a) = 1 – р(А) = 1 – 0,22326 = 0,7764.

4. Используя формулу Харди-Вайнберга: p 2 + 2pq + q 2 = 1 = 100%, рассчитаем частоту встречаемости рецессивных гомозигот (аа) в популяции гречихи, получим:

p 2 (AA) + 2pq(Aa) + q 2 (aa) = 1 = 100%;
q 2 (aa) = (0,7764) 2 = 0,6028 или 60,28%.

Ответ:
р 2 (АА) = 0,05 или 5%;
q 2 (aa) = 0,6028 или 60,28%.

Использование формулы Харди-Вайнберга для расчета фенотипов у кроликов

Задача 384.
У кроликов окраска волосяного покрова “шиншилла” доминирует над альбинизмом. Гетерозиготы имеют светло-серую окраску. На кролиководческой ферме среди молодняка кроликов шиншилл появились альбиносы. Из 8100 крольчат 25 оказались альбиносами. Пользуясь формулой Харди-Вайнберга, определите, сколько было получено гетерозиготных крольчат, имеющих светло-серую окраску и сколько гомозиготных крольчат, имеющих окраску “шиншилла”.
Решение:
А — окраска волосяного покрова “шиншилла”;
а — альбинизм;
Аа — гетерозигота — светло-серая окраса шерсти;
N_общ. = 8100 крольчат;
крольчата-альбиносы = 25 шт.;
p 2 (AA) = ?
2pq(Aa) = ?
q 2 (aa) = 25/8100 = 0,003086.

Зная частоту встречаемостигомозигот (аа) рассчитаем частоту аллеля (а)

q(а) = √0,003086 = 0,056.

Согласно первому следствию закона Харди-Вайнберга рассчитаем частоту встречаемости гена (А), получим:

р + q = 1, р(А) = 1 — q(а) = 1 — 0,0556 = 0,9444.

Используя формулу Харди-Вайнберга: р 2 + 2рq + q 2 = 1, рассчитаем фенотипическую структуру данной популяции кроликов, получим:

р 2 (АА) + 2рq(Аа) + q 2 (аа) = 1 = 100%;
(0,9444) 2 + (2 • 0,9444 • 0,0556) + ( 0,0556) 2 = 1 = 100%;
0,89189 или 89,2%(АА) + 0,1050 или 10,5%(Аа) + 0,00309 или 0,3%(аа) = 1 или 100%.

Рассчитаем число светло-серых крольчат, получим:

N_{(светло-серые крольчата)} = 8100 • 0,105 = 850,5 примерно 850 шт.

Рассчитаем число крольчат с окраской «шиншила», получим:

N_{(«шиншиловые» крольчата)} = 8100 • 0,892 = 7225,2 примерно 7225 шт.

Ответ:
N_{(светло-серые крольчата)} = 850 шт;
N_{(«шиншиловые» крольчата)} = 7225 шт.

Видео:Уравнение Харди-ВайнбергаСкачать

Решение задач по теме «Генетика популяций. Закон Харди-Вайнберга»
материал для подготовки к егэ (гиа) по биологии (11 класс) на тему

В линии 28 на ЕГЭ по биологии учащимся предлагаются различные биологические задачи по генетике, образцов решения которых нет в учебниках, в том числе, и на закон Харди-Вайберга. В работе представлены 3 задачи с анализом ответов и 5 задач для самостоятельного решения.

Видео:Такого на ЕГЭ по биологии еще не было! Закон Харди-Вайнберга | Биология ЕГЭ 2024 | УмскулСкачать

Скачать:

Вложение	Размер
genetika_populyatsiy.docx	27.76 КБ

Видео:ПОЛНЫЙ РАЗБОР ХАРДИ-ВАЙНБЕРГА // РЕШЕНИЕ ЗАДАЧ ОТ BioFamily (ЕГЭ-2024 БИОЛОГИЯ)Скачать

Предварительный просмотр:

МБОУ «Карагайская СОШ № 2»

с. Карагай, Пермский край

по теме «Генетика популяций.

Закон Харди – Вайнберга»

ЕГЭ. Биология, 11 класс.

Решение задач линии 28.

Трефилова Раиса Поликарповна,

МБОУ «Карагайская СОШ № 2»

Цель: Дать рекомендации учащимся по выполнению задания линии 28 при подготовке к ЕГЭ.

1. Информировать учащихся 11 класса о требованиях к выполнению заданий линии 28 по биологии.

2. Познакомить с кодификатором, спецификацией и образцами заданий.

3. Мотивировать учащихся к успешной подготовке к ЕГЭ.

Теоретическое обоснование темы

Начальные этапы эволюционных процессов протекают в популяциях на основе закономерностей наследования. Изучение генетической структуры популяции связано с выяснением генотипического состава. В подобных задачах определяется частоты генотипов и аллелей, которые выражаются в % или в долях от единицы. Данная закономерность была выявлена независимо друг от друга двумя исследователями: математиком Г.Харди и врачом В.Вайнбергом.

«Относительные частоты генов в популяции не изменяются из поколения в поколение во времени при следующих условиях:

Популяция должна быть велика;
Отсутствует давление отбора на данные признаки;
Отсутствуют мутации этих генов;
В популяции особи свободно скрещиваются;
Нет миграции из соседних популяций».

Предположим некую популяцию с одинаковым соотношением генотипов АА и аа. Частоту генов А (A большое-доминантный признак ) обозначим р, а гена а (а малое – рецессивный признак) – q.

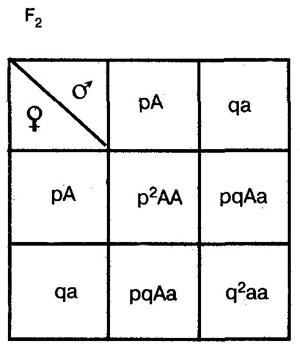
На основании скрещивания составляем решётку Пеннета.

♂

p² (AA) + 2 pq (Aa) + q² (aa) = 1

p + q = 1 (при извлечении квадратного корня)

Сумма частот генов в популяции p + q = 1, следовательно, уравнение можно рассмотреть как: p² + 2 pq + q² = 1

Закон Харди-Вайнберга может быть сформулирован следующим образом:
«В идеальной популяции соотношение частот аллелей генов и генотипов из поколения в поколение является величиной постоянной и соответствует уравнению: p 2 +2pq + q 2 = 1
где p 2 — доля гомозигот по доминантной аллели; p — частота этой аллели; q 2 — доля гомозигот по альтернативной аллели; q — частота соответствующей аллели; 2pq — доля гетерозигот.

Закон Харди-Вайнберга при медико-генетических исследованиях, а также при определении частоты генов, генотипов и фенотипов в популяциях в природе, популяций в животноводстве и селекции. В этом его практическое значение.

Рассмотрим решение нескольких вариантов задач по данной теме.

Задача 1. В популяции человека количество индивидуумов с карим цветом глаз составляет 51%, а с голубым – 49%. Определите процент доминантных гомозигот в данной популяции.

Поскольку известно, что карий цвет глаз доминирует над голубым, обозначим аллель, отвечающую за проявление признака кареглазости А, а аллельный ему ген, ответственный за проявление голубых глаз, соответственно, а. Тогда кареглазыми в исследуемой популяции будут люди как с генотипом АА (доминантные гомозиготы, долю которых и надо найти по условию задачи), так и — Аа гетерозиготы), а голубоглазыми – только аа (рецессивные гомозиготы).
По условию задачи нам известно, что количество людей с генотипами АА и Аа составляет 51%, а количество людей с генотипом аа — 49%. Как можно вычислить процент кареглазых людей только с генотипом АА?
Для этого вычислим частоты встречаемости каждого из аллельных генов А и а в данной популяции людей. Обозначив частоту встречаемости аллели А в данной популяции буквой q, имеем частоту встречаемости аллельного ему гена а = 1 – q. (Можно было бы обозначить частоту встречаемости аллельного гена а отдельной буквой, как в тексте выше – это кому как удобнее). Тогда сама формула Харди-Вайнберга для расчета частот генотипов при моногибридном скрещивании при полном доминировании одного аллельного гена над другим будет выглядеть вот так:
q 2 AA+ 2q(1 – q)Aa + (1 – q) 2 aa = 1.
(1 – q) 2 = 0,49 – это частота встречаемости людей с голубыми глазами.
Находим значение q: 1 – q = корень квадратный из 0,49 = 0,7; q = 1 – 0,7 = 0,3, тогда q ² = 0,09.
Это значит, что частота кареглазых гомозиготных особей АА в данной популяции будет составлять 0,09 или доля их будет равна 9%.

Ответ: частота кареглазых гомозиготных особей АА равна 9 %.

Задача 2. В популяции озёрной лягушки появилось потомство – 420 лягушат с тёмными пятнами (доминантный признак) и 80 лягушат со светлыми пятнами. Определите частоту встречаемости рецессивного гена и число гетерозигот среди лягушек с тёмными пятнами.

Записываем условие задачи. Тёмный цвет пятен обозначаем А, светлый цвет пятен – а. Необходимо определить генотипы родительских форм.

Признак, фенотип Ген, генотип

Светлые пятна а

F: 420 лягушат с темн. Пятнами А_

80 лягушат со светл. пятнами аа

1. Каково количество особей в популяции?

2. Определяем частоту встречаемости лягушат со светлыми пятнами — q²

q²= 80: 500 = 0, 16 (частота встречаемости аллели равна отношению числа данной аллели к общему числу аллелей в популяции)

3. Определяем частоту встречаемости рецессивного гена «светлое пятно» «а малое», который мы обозначили q:

q = √ q² = √ 0,16 = 0,4

4. Определяем частоту встречаемости гена «тёмные пятна»(т.е. ), исходя из уравнения р + q = 1, значит, р = 1 – q, следовательно, р = 1 – 0,4 = 0,6

5. Определяем количество гетерозигот Аа :

2рq = 2х0,4 х 0,6 = 0, 48 или 48 %

Объяснение решения задачи: для решения задачи используется закон Харди-Вайнберга.

1) Число особей в популяции – 500.

2) Частота встречаемости рецессивного гена а «светлое пятно» — 0,4.

3) Количество гетерозигот (Аа) носителей гена «светлые пятна» — 0, 48 или 48%.

Задача 3. Популяция состоит из 49 % особей с генотипом АА и 9 % с генотипом аа. Находится ли эта популяция в равновесии?

Признак, фенотип Ген, генотип

р = 49 % или 0,49 АА

q = 9 % или 0, 09 аа

1. Если популяция находится в равновесии, то для неё справедливо уравнение Харди – Вайнберга:

2. Для данной популяции частота генотипа АА : p² = 0,49,

частота аллеля А : √ 0,49 = 0, 7 ; р = 0,7

3. Определяем частоту генотипа аа : q² = 0,09, тогда

частота аллеля а : q =√ 0,09 = 0,3.

4. Определяем частоту генотипа гетерозиготы Аа: 2 pq = 2 х 0,7 х 0,3 = 0,42

5. Определяем, находится ли популяция в равновесии: если

p² + 2 pq + q² = 1, то 0,49 + 0,42 + 0,09 = 1, следовательно, популяция находится в равновесии.

По уравнению Харди-Вайнберга сумма равна 1, популяция находится в равновесии.

Задачи для самостоятельного решения

1. В Европе на 10 000 человек с нормальным содержанием меланина встречается 1 альбинос. Ген альбинизма наследуется по аутосомно-рецессивному типу. Рассчитать частоту встречаемости носителей гена альбинизма. Носителем называют организм, гетерозиготный по гену, который может вызвать в гомозиготном состоянии нарушение метаболизма.

Ответ: частота встречаемости гетерозигот 2 pq = 0,0198 или почти 2%

2. Предрасположенность к сахарному диабету наследуется по аутосомно-рецессивному типу. Частота встречаемости рецессивного гена предрасположенности к болезни в США приблизительно 22, 5 %. Какова частота встречаемости в США гетерозиготных носителей гена предрасположенности к сахарному диабету.

Ответ: частота встречаемости в США гетерозиготных носителей гена предрасположенности к сахарному диабету равна 0,4982.

3. У человека ген «резус положительный» доминантен по отношению к гену «резус отрицательный». В обследованной по этому показателю популяции 1982 человека были «резус положительными», а 368 – «резус отрицательными». Какова генетическая структура этой популяции?

4. У гречихи ярко-красная окраска растений неполно доминирует над зелёной. Гетерозиготы по данным генам имеют розовую окраску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?

Ответ: частота встречаемости гомозиготных растений = 0,657.

5. Одна из форм глюкозурии наследуется как аутосомно-рецессивный признак и встречается с частотой 7:1000000. Определить частоту встречаемости гетерозигот в популяции.

Ответ: частота встречаемости гетерозиготных особей 2pq в популяции людей = 0,0052775.

1. Гончаров О.В. Генетика.Задачи. – Саратов: Лицей, 2008.

2. Кириленко А.А. Биология. Сборник задач по генетике. Базовый и повышенный уровень ЕГЭ: учебно-методическое пособие/А.А.Кириленко. – Ростов-на-Дону: Легион, 2009.

3. Кириленко А.А., Колесников С.И. Биология. Подготовка к ЕГЭ-2013: учебно-методическое пособие/А.А.Кириленко, С.И.Колесников. – Ростов-на-Дону: Легион, 2012.

Видео:РЕШЕНИЕ ЗАДАЧИ ЛИНИИ 27 НА УРАВНЕНИЕ ХАРДИ-ВАЙНБЕРГАСкачать

По теме: методические разработки, презентации и конспекты

Урок физики в 9 классе: «Решение задач по теме «Импульс. Закон сохранения импульса»

Урок повторения и закрепления знаний по теме «Импульс. Закон сохранения импульса» Учащимся после повторения и самопроверки предлагаются задачи разного типа и уровня сложности, алгоритм решения типовых.

Решение задач по теме «Первый закон термодинамики».

Данный материал создан на основе программы Notebook 10 для интерактивной доски. Содержание включает пять задач разной степени сложности с решениями.Используется на уроках в 10 классе базового уро.

разработка урока «Закон Харди-Вайнберга»

Разработка урока может быть использована при изучении темы «Популяционная генетика» для изучении биологии на углубленном уровне и на дополнительных занятиях при подготовке детей к ЕГЭ на базовом уровн.

Решение задач по теме «Второй закон Ньютона». Составление практического задания к компьютерной модели «Движение тел на легком блоке».

Решение задач по теме «Второй закон Ньютона».Составление практического задания к компьютерной модели «Движение тел на легком блоке».(Использование компьютерных технологий на уроках ф.

Разработка урока: Решение задач по теме «Газовые законы»

В разработке урока присутствует повторение темы «Газовые законы». Рассматривается решение качественных и экспериментальных задач. экспериментальные задачи сопровождаются проведением простых опытов с и.

презентация Закон Харди-Вайнберга

Презентация «Генетическое равновесие в популяциях и его нарушение» знакомит учащихся с понятием «популяционная генетика», законом Харди-Вайнберга. Помогает научиться решать разные типы зад.

Решение задач по теме «Генетика популяций. Закон Харди – Вайнберга»

Видео:Закон Харди-Вайнберга - наглядное объяснение | Закон генетического равновесияСкачать

Решение задач по теме «Закон Харди-Вайнберга»

Для того чтобы описывать генетические свойства популяции, вводится понятие генофонда: совокупности генов, встречающихся в данной популяции. Помимо генофонда важны также частота встречаемости гена или частота встречаемости аллеля.

Знание того, как реализуются законы наследования на уровне популяций, принципиально важно для понимания причин индивидуальной изменчивости. Все закономерности, выявляемые в ходе психогенетических исследований, относятся к конкретным популяциям. В других популяциях, с иным генофондом и другими частотами генов, могут получаться отличающиеся результаты.

Закон Харди-Вайнберга— основа математических построений генетики популяций и современной эволюционной теории.

Данная разработка содержит теоретический материал по теме и примеры решения задач на применение данного закона.

Просмотр содержимого документа
«Решение задач по теме «Закон Харди-Вайнберга»»

Популяционная генетика занимается генетической структурой популяций.

Понятие «популяция» относится к совокупности свободно скрещивающихся особей одного вида, длительно существующей на определенной территории (части ареала) и относительно обособленной от других совокупностей того же вида.

Важнейший признак популяции — это относительно свободное скрещивание. Если возникают какие-либо изоляционные барьеры, препятствующие свободному скрещиванию, то возникают новые популяции.

У человека, например, помимо территориальной изоляции, достаточно изолированные популяции могут возникать на основе социальных, этнических или религиозных барьеров. Поскольку между популяциями не происходит свободного обмена генами, то они могут существенно различаться по генетическим характеристикам. Для того чтобы описывать генетические свойства популяции, вводится понятие генофонда: совокупности генов, встречающихся в данной популяции. Помимо генофонда важны также частота встречаемости гена или частота встречаемости аллеля.

Закон Харди-Вайнберга— основа математических построений генетики популяций и современной эволюционной теории. Сформулирован независимо друг от друга математиком Г. Харди (Англия) и врачом В. Вайнбергом (Германия) в 1908 г. Этот закон утверждает, что частоты аллелей и генотипов в данной популяции будут оставаться постоянными из поколения в поколение при выполнении следующих условий:

1) численность особей популяции достаточно велика (в идеале — бесконечно велика),

2) спаривание происходит случайным образом (т. е. осуществляется панмиксия),

3) мутационный процесс отсутствует,

4) отсутствует обмен генами с другими популяциями,

5) естественный отбор отсутствует, т. е. особи с разными генотипами одинаково плодовиты и жизнеспособны.

Иногда этот закон формулируют иначе: в идеальной популяции частоты аллелей и генотипов постоянны. (Поскольку описанные выше условия выполнения данного закона и есть свойства идеальной популяции.)

Математическая модель закона отвечает формуле:

Она выводится на основе следующих рассуждений. В качестве примера возьмем простейший случай — распределение двух аллелей одного гена. Пусть два организма являются основателями новой популяции. Один из них является доминантной гомозиготой (АА), а другой — рецессивной гомозиготой (аа). Естественно, что все их потомство в F₁ будет единообразным и будет иметь генотип (Аа). Далее особи F₁ будут скрещиваться между собой. Обозначим частоту встречаемости доминантного аллеля (А) буквой p, а рецессивного аллеля (а) — буквой q. Поскольку ген представлен всего двумя аллелями, то сумма их частот равна единице, т. е. р + q = 1. Рассмотрим все яйцеклетки в данной популяции. Доля яйцеклеток, несущих доминантный аллель (А), будет соответствовать частоте этого аллеля в популяции и, следовательно, будет составлять р. Доля яйцеклеток, несущих рецессивный аллель (а), будет соответствовать его частоте и составлять q. Проведя аналогичные рассуждения для всех сперматозоидов популяции, придем к заключению о том, что доля сперматозоидов, несущих аллель (А), будет составлять р, а несущих рецессивный аллель (а) — q. Теперь составим решетку Пеннета, при этом при написании типов гамет будем учитывать не только геномы этих гамет, но и частоты несомых ими аллелей. На пересечении строк и столбцов решетки мы получим генотипы потомков с коэффициентами, соответствующими частотам встречаемости этих генотипов.