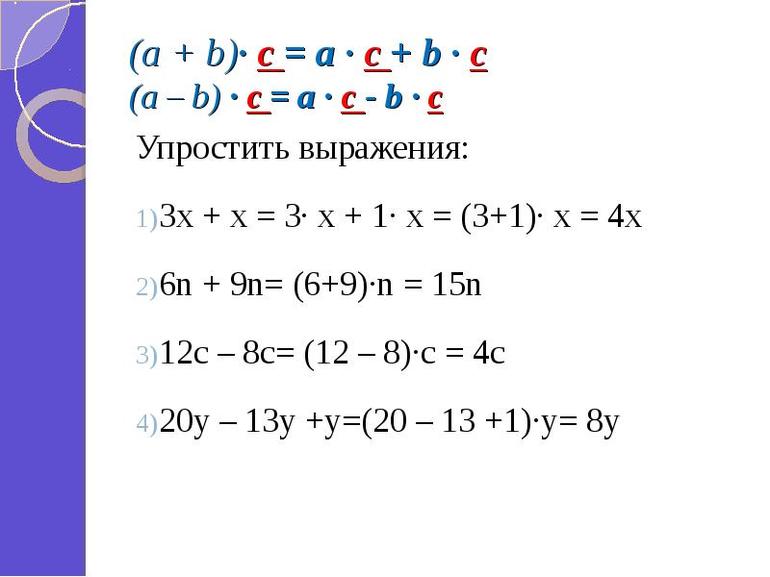Как решить уравнения с упрощением 5 класс (7 видео)

Упрощение выражений

Содержание

Содержание
Правила упрощения
Решение уравнений с применением упрощения выражений
Урок математики «Упрощение выражений. Решение уравнений и текстовых задач». 5-й класс
Упрощения выражений — формулы и примеры для 5 класса
Общие сведения
Базовые знания
Приведение подобных элементов
Раскрытие скобок
Работа со степенями
Оптимизация обыкновенных дробей
Сокращенное умножение
📸 Видео

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Содержание

В математическом мире существует большое количество выражений, которых трудно решить без упрощения. Помимо этого, упрощение математических примеров используется для того, чтобы быстрее и правильнее решить задание.

Давайте рассмотрим пример, и не забывайте, что для этого нам понадобятся знания правил умножения, вычитания и сложения:

В данном случае, сначала мы можем посчитать сумму в скобках, а затем умножить на 3. Но далеко не всегда такой способ будет удобным при решении задач. Если цифры будут слишком большими — это будет попросту неудобно. Для облегчения решения нам нужно будет упростить данное выражение. Теперь рассмотрим пример его упрощения:

Сейчас мы видим, что выражение значительно изменилось. При этом, ответ будет точно таким же, как и в первом случае. Такой вид выражения не только легче и быстрее решать, но и помогает избежать ошибок при вычислении. Итак, как же правильно следует применять правила упрощения выражений и как решать уравнения с их помощью?

Видео:Уравнение. 5 класс.Скачать

Правила упрощения

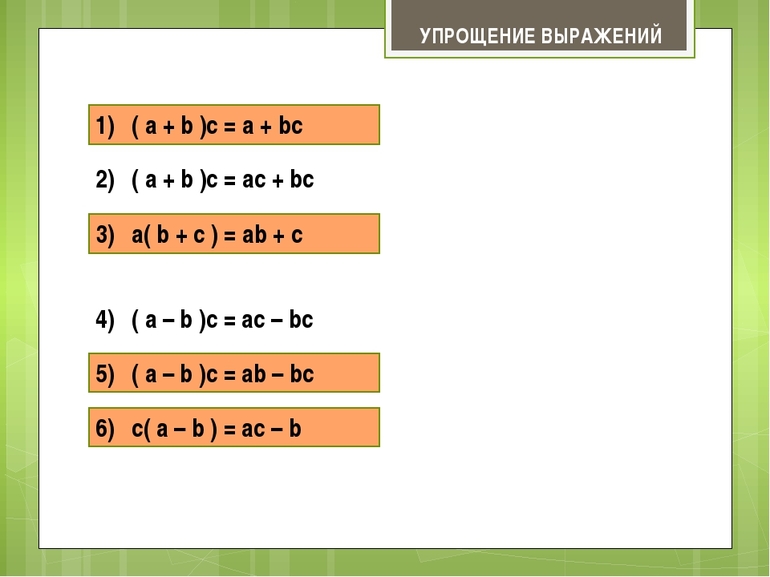
Существует всего два правила по упрощению выражений с умножением. Их называют распределительными свойствами умножения относительно сложения и вычитания. Давайте их разберем:

Для того чтобы умножить сумму на число, нужно умножить на это число первое и второе слагаемое, а затем сложить получившиеся произведения.

С помощью букв данное правило записывают так: $(a+b)cdot c=ac+bc$

Если нам нужно умножить разность на число, то следует умножить на это число уменьшаемое и вычитаемое, а потом из первого произведения вычесть второе.

Буквенное выражение данного свойства выглядит следующим образом: $(a-b)cdot c=ac-bc$

Видео:Упрощение выражений. 5 класс.Скачать

Решение уравнений с применением упрощения выражений

Правила упрощения выражений работают и в обратную сторону, то есть позволяют вынести разность или сумму в скобки, а число, на которое нужно умножить — за скобки. Именно поэтому их используют для решения уравнений. Разберем на примере:

Для того чтобы сложить два числа с $x$, нам нужно применить уже изученное нами распределительное свойство:

Благодаря данному упрощению мы сможем до конца решить наше уравнение:

Видео:Математика 5 класс. Уравнение. Корень уравненияСкачать

Урок математики «Упрощение выражений. Решение уравнений и текстовых задач». 5-й класс

Разделы: Математика

Класс: 5

Цели урока:

Образовательные – совершенствовать умения упрощать выражения, применять их при решении уравнений и текстовых задач;
Развивающие – развивать познавательный интерес к математике, память учащихся, умения организовывать свой труд;
Воспитательные – воспитывать самостоятельность, аккуратность, потребность к приобретению знаний

Тип урока: урок совершенствования знаний, умений и навыков

Формы организации деятельности учащихся: фронтальная, групповая.

Планируемые результаты обучения:

Предметные: уметь в процессе реальной ситуации применять упрощение выражений.
Личностные: упрощают выражения, используют свойства умножения, применяют рациональные приёмы для вычислений, формируют внимательность и аккуратность в вычислениях, требовательное отношение к себе и к своей работе.
Познавательные: закрепляют навыки и умения применять правила упрощений выражений при решении задач на умножение натуральных чисел и применение свойств умножения, систематизируют знания, обобщают и углубляют знания, выбирают и формулируют познавательную цель, выражают смысл ситуации с помощью различных примеров.
Регулятивные:
Планируют собственную деятельность, определяют средства для её осуществления.
Коммуникативные: регулируют собственную деятельность посредством речевых действий, умения слушать и вступать в диалог, воспитывать чувство взаимопомощи. Уважительное отношение к чужому умению, культуру учебного труда, требовательное отношение к себе и своей работе.

I. Организационный момент

Цель: подготовить учащихся к работе на уроке

Посмотрите, все ль в порядке:
Книжка, ручки и тетрадки.
Прозвенел сейчас звонок,
Начинается урок.

II. Мотивация учебной деятельности

Цель: создать условия для формирования у учеников внутренней потребности во включение в учебную деятельность.

Учитель: Здравствуйте, ребята! Начать урок я хочу с вопроса к вам. Как вы думаете, что самое ценное на Земле?

(Выслушиваются варианты ответов учеников)

Учитель: Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный учёный Ал — Бируни: «Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит». Пусть эти слова станут девизом нашего урока.

III. Проверка домашнего задания

Соседи по парте обмениваются тетрадями, проверяют домашнее задание по интерактивной доске и карандашом ставят оценку (Презентация, слайд 1)

IV.Актуализация опорных знаний и умений учащихся

Цель: подготовить учащихся к деятельности на основном этапе урока;-развивать логическое мышление, умения обобщать, классифицировать, строить
умозаключения.

Учитель: Определите, какое слово лишнее в данных заданиях (слайд 2)

а) Километр, метр, сантиметр, длина, миллиметр, дециметр.

Ученики: длина.

б) Тонна, центнер, масса, грамм, пуд.

Ученики: масса.

Учитель: В каком отношении находится лишнее слово в каждом из списков?

Ученики: В случае а) километр, метр, сантиметр, миллиметр, дециметр – единицы измерения длины, а в случае б) тонна, центнер, грамм, пуд – единицы измерения массы.

1. Упростите выражения (слайд 3)

4а + 8а 30р – 12р
6х + 8х + х 8у – 3у – у
9с + 4с + 7с 5у + 2у
8а – а – а

Учитель: Какие свойства умножения применили при упрощении выражений?

Ученики: Распределительное свойство умножения относительно сложения и вычитания.

Учитель: Запишите эти свойства на доске.

Учитель: Общаясь в парах по парте, вспомните правила нахождения неизвестного компонента в уравнении и решите его (слайд 4).

(Уравнения по одному появляются на слайдах. После обсуждения в парах, проверяется правильность решения уравнений)

а) х + 15=40; в х : 20 = 3;
б) у – 10 = 32; г) 25х = 100

Учитель: Как вы думаете, какова тема сегодняшнего урока?

Ученики: Упрощение выражений, решение уравнений.

Учитель: (уточняет тему) Упрощение выражений, решение уравнений и текстовых задач.

Учитель: Каковы цели урока?

Ученики: Научиться безошибочно упрощать выражения, применять эти умения при решении уравнений и текстовых задач.

V. Усвоения новых знаний

Цель: Организовать деятельность учащихся по усвоению новых способов действий.

Учитель: Откройте тетради, запишите дату и тему урока «Упрощение выражений. Решение уравнений и текстовых задач» (слайд 5)

Учитель: Прочитайте выражение.
Ученики: Сумма выражений 7а и 42а и числа 5.
Учитель: Назовите слагаемые этой суммы
Ученики: 7а, 5, 42 а
Учитель: Какие из них можно объединить? По какому признаку?
Ученики: 7а и 42 а, так как у них одинаковая буква.
Учитель: Совершенно верно! Эти слагаемые содержат одинаковую букву, поэтому их называют подобными. Для удобства упрощения подобные слагаемые можно подчеркнуть.

Учитель: Что можно сделать с подчеркнутыми слагаемыми?
Ученики: Применить распределительное свойство умножения относительно сложения.

Учитель: Решим уравнение

Учитель: Каков первый шаг в решении уравнения?
Ученики: Подчеркнуть подобные слагаемые и упростить левую часть уравнения.
Учитель: Какое уравнение получим?
Ученики: 10у + 25 = 85
Учитель: Проговорите названия компонентов действия.
Ученики: 10у – первое слагаемое, 25 – второе слагаемое, 85 – сумма.
Учитель: Дорешайте уравнение ( Один ученик работает у доски, комментируя решение)

10у = 85 – 25
10 у = 60
х = 60 : 10
х = 6
Ответ: 6

Учитель: Откройте страницу 88 учебника и прочитайте задачу № 578 (работа с учебником, разбор решенной задачи).
Учитель: Какие произведения напечатаны в книге?
Ученики: Рассказ и повесть.
Учитель: Сколько в книге страниц?
Ученики: 70 страниц.
Учитель: Сколько страниц занимает повесть?
Ученики: Неизвестно, но в 4 раза больше, чем рассказ.
Учитель: Каков вопрос задачи?
Ученики: Сколько страниц занимает рассказ и сколько повесть?
Учитель: Чем отличается эта задача от тех, что мы решали уравнением?
Ученики: В вопросе два неизвестных числа.
Учитель: Запишем краткое условие задачи
Учитель: Какую величину в задаче удобно обозначить за х?
Ученики: Меньшую величину. Пусть х – количество страниц в рассказе.
Учитель: Сколько страниц занимает повесть?
Ученики: 4х страниц
Учитель: В условии сказано, что рассказ и повесть вместе занимают 70 страниц. Как составить уравнение?
Ученики: х + 4х = 70
Учитель: Решите уравнение

Учитель: Что означает найденный корень уравнения?
Ученики: 14 страниц занимает рассказ
Учитель: Как найти, сколько страниц занимает повесть?
Ученики: 14 • 4 = 56 (с.) – занимает повесть.
Учитель: Запишите ответ задачи.

VI. Пробное применение знаний

Цель: развивать коммуникативные навыки учащихся

Учитель: У доски выполним задание №574 (Два ученика работают у доски по очереди, подробно объясняя ход решения, остальные учащиеся решают в тетрадях, слушая комментарии учеников у доски).

а) 3x + 7x + 18 = 178 б) 6у – 2у + 25 = 65
10х + 18 = 178 4у + 25 = 65
10х = 178 – 18 4у = 65 – 25
10 х = 160 4у = 40
х = 160 : 10 у = 40 : 4
х = 16 у = 10
Ответ: 16 Ответ: 10

VII.Физкультминутка

Поднимает руки класс
Это «раз», (Потягивания под счет учителя.)
Повернулась голова —
Это «два». (Движения головой.)
Руки вниз, вперед смотри –
Это «три». (Приседания.)
Руки в стороны пошире
Развернули на «четыре». (Повороты туловища.)
С силой их к плечам прижать —
Это «пять». (Движения руками.)
Всем ребятам тихо сесть —
Это «шесть».

Учитель: Прочитайте задачу №580 и обсуждая в парах, решите её (слайд 9)

х + 9х = 220
х = 22 ( столов)
22*9 = 198 (стульев)
Ответ: 22 стола и 198 стульев

(Проверяют решение с доски, слайд 7)

Учитель: Выполним творческое задание на составление задачи по уравнению №594(а)

(Учащиеся выполняют самостоятельно, потом желающие прочитывают свою задачу классу)

VI. Проверка знаний

Цель: Проверить уровень усвоения знаний по теме, определить недостатки, ликвидировать пробелы.

Учитель: Выполните тест,ответы запишите в бланках. (Приложение 1)

VII. Рефлексия

Цель: способствовать формированию умения анализировать собственную деятельность по достижению поставленной цели.

Учитель: Наше занятие подходит к концу. Пожалуйста, поделитесь своими мыслями о сегодняшнем уроке (Приложение 2)

1. Я умею упрощать выражения (да, нет).
2. Я умею решать уравнения (да, нет).
3. Сегодня на уроке мне было …
4. Трудности возникли при …
5. Мне помог преодолеть трудности …

VIII. Домашнее задание

1) Для обязательного выполнения №614 (в,г) , 618
2) Для выполнения по желанию учащихся (на карточке, Приложение 3)
Пусть записано подряд семь цифр от 1 до 7: 1234567
Легко соединить их знаками «плюс» и «минус» так, чтобы получилось 40:

12 + 34 – 5 + 6 – 7 = 40

Попробуйте найти другие расстановки знаков между теми же цифрами, при которых получилось бы не 40, а 55.

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Упрощения выражений — формулы и примеры для 5 класса

Видео:Уравнения. 5 классСкачать

Общие сведения

Принцип решения любой математической задачи основан на получении оптимального ответа, который в дальнейшем возможно будет применить для других целей (доказательства теорем, тождеств, получения промежуточных величин). Оптимизация результата состоит из операций, имеющих собственный приоритет. Последний соответствует порядковому номеру элемента в списке:

Раскрытие скобок.
Возведение в степень, которая может быть целой и представленной в виде обыкновенной дроби (корень).
Произведение.
Частное или деление.
Сумма.
Разность.

В первом случае компоненты выражения группируются посредством скобок. В математике принято использовать только круглые, т. е. «()». Однако допускаются квадратные «[]», но некоторые начинающие математики иногда группируют элементы выражения при помощи фигурных скобок «». Это делать не рекомендуется, поскольку последние обозначают в дисциплинах с физико-математическим уклоном общее решение.

Иногда новички не знают, что возведение в степень и извлечение корня являются двумя эквивалентными операциями. Это утверждение легко доказывается. Например, квадратный корень из 36 эквивалентен 6. Знак радикала можно заменить степенью, имеющей вид обыкновенной или десятичной дроби, т. е. (36)^(½)=√36=6.

Произведение не всегда обладает высшим приоритетом, чем деление. Для удобства вычислений можно сначала разделить, а затем умножить. Например, требуется найти значение выражения «3*81:9». Его можно решить, основываясь на приоритетах или удобстве вычислений (оптимизации). Для сравнения расчетов нужно решить равенство двумя способами:

При решении получены одинаковые результаты. Следует отметить, что простой метод — второй. Операции сложения и вычитания имеют одинаковый приоритет. Упростить выражение — означает, что необходимо преобразовать его из сложной формы представления в простую. Иными словами, операция называется оптимизацией результата.

Оптимизация выражений применяется при решении уравнений (равенств с неизвестными величинами) любой сложности и доказательства теорем. Это базовые знания, необходимые для упрощения выражений в 5 классе.

Видео:Упрощение буквенных выражений 5 класс.Скачать

Базовые знания

Для освоения определенного направления в любой дисциплине необходимы определенные знания. Например, невозможно выполнить умножение одного числа на другое, не зная таблицы умножения. Это касается и оптимизации тождеств. Основные элементы теории, которые нужно знать для выполнения операции:

Приведение общих компонентов.
Правила раскрытия скобок.
Работа со степенями.
Действия над знаменателями обыкновенных дробей и их сокращение.
Соотношения сокращенного умножения.

По этим пунктам можно упрощать алгебраические целочисленные и дробные выражения любой сложности. Однако каждый из элементов необходимо разобрать подробно, чтобы не совершать ошибок при расчетах.

Приведение подобных элементов

Практически во всех заданиях нужно складывать общие элементы, полученные при расчетах или раскрытии скобок. Для этой операции необходимо руководствоваться следующими правилами:

Приведению подлежат только эквивалентные компоненты.
Операция выполняется только при арифметическом сложении и вычитании, а не делении и умножении.
Компоненты равные по модулю, но противоположные по знаку, уничтожаются, т. к. в сумме дают нулевое значение.
В любом выражении можно использовать противоположные числа, поскольку их общее значение не влияет на результат.

В первом случае нужно привести пример тождества следующего вида: 2+5t+4+5t^2+2t-4t^2. Чтобы его упростить, необходимо сгруппировать подобные компоненты, т. е. (2+4)+(5t+2t)+(5t^2-4t^2). Далее следует сложить компоненты между собой, т. е. 6+7t+t^2.

Группу «5t^2-4t^2» можно назвать операцией сложения, хотя на самом деле она называется разностью, которую записывают и в виде суммы: 5t^2+(-4t^2). Раскрывая скобки в последнем тождестве, можно получить упрощенную форму: 5t^2-4t^2. Далее необходимо ознакомиться с правилами раскрытия скобок.

Раскрытие скобок

Операция раскрытия скобок для выполнения дальнейших вычислений очень часто применяется в различных дисциплинах с физико-математическим уклоном. Она осуществляется по следующим правилам:

Произведение на сумму или разность: r(s+t)=rs+rt или r(s-t)=rs-rt.
Деление суммы или разности: (s+t)/r=s/r+t/r или (s-t)/r=s/r-t/r.
Сгруппировать любые компоненты и поменять их местами с сохранением логики тождества: 3+4+11+7+19+33+23=(3+4+23)+(19+11)+(7+33)=30+30+40=100.

В первом и втором случаях операции называют вынесением общего множителя за скобки. Последнее правило группировки действует не на все компоненты, т. е невозможно выполнить объединение 2 и 3 элементов (5 и 4) в выражении «4:5+4-1+7». Для доказательства следует решить его двумя способами:

Выражение, решенное первым и вторым способом, имеет различные ответы, поскольку 10,8>6[4/9]. Объяснение этому несоответствию — нарушение логики тождества. Следующим компонентом, составляющим базу для упрощения тождеств, является работа со степенями.

Работа со степенями

В математических тождествах иногда необходимо упростить степенные выражения. Однако большинство математиков-новичков делает много ошибок, поскольку не знают основных правил:

Нулевое значение в такой же степени является пустым множеством, т. е. его не существует. Cтепень может быть представлена в виде обыкновенной или десятичной дроби. В последнем случае для удобства ее необходимо перевести к первому типу. Если указано значение степенного показателя, равное 3/5, нужно величину возвести в куб, а затем изъять корень 5 порядка.

Оптимизация обыкновенных дробей

Практически во всех заданиях или тренажерах большая часть примеров представлена в виде обыкновенной дроби вида s/t, которую нужно сократить. Иногда необходимо произвести операции произведения или деления одной величины на другую (буквенное обозначение — s/t и w/v), а также сложения и вычитания. При последних операциях всегда необходимо приводить дробные тождества к общему знаменателю. Эта операция осуществляется следующим образом:

Если знаменатель одной дроби делится нацело на другой, следует оставить первый, записав множитель над второй величиной. Например, 4/5 + 4/25=(4*5+4*1)/25=24/25.
Когда v и t не делятся друг на друга, не имеют общих множителей, их нужно перемножить между собой, записав множители над числителями.
Если v и t содержат общие множители, единый знаменатель эквивалентен наименьшему общему кратному (НОК).

В последнем случае каждый знаменатель необходимо разложить на множители, затем перемножить между собой все неповторяющиеся компоненты. Следующим элементом, который необходимо для преобразования тождеств, являются формулы сокращенного умножения.

Сокращенное умножение

Для решения задач очень часто применяются формулы сокращенного умножения. В некоторых случаях тождества «собираются» в них или, наоборот, для сокращения нужно расписать элементы по множителям (правая часть равенства). Соотношения имеют следующий вид:

Квадрат суммы и разности двух чисел: (w+v)^2=w^2+2wv+v^2 и (w-v)^2=w^2-2wv+v^2.
Разность квадратов и кубов: w^2-v^2=(w+v)(w-v) w^3-v^3=(w-v)(w^2+wv+v^2).
Куб суммы компонентов и их разности: (w+v)^3=w^3+3wv^2+3vw^2+v^3 и (w-v)^3=w^3-3wv^2+3vw^2-v^3.

Cледует отметить, что в некоторых случаях к формуле сокращенного умножения тождество следует «подвести», воспользовавшись свойством отнимания и прибавления одного и того же значения. Например, необходимо из некоторого выражения (2t^2-60) выделить одну из формул. Это делается следующим образом:

Выносится общий множитель за скобки: 2(t^2-30).
Прибавляется и отнимается 6: 2(t^2-30+6-6).
Группируются элементы и записывается формула: 2(t^2-36+6)=2[(t-6)(t+6)+6].

Иногда в более сложных выражениях приходится применять несколько соотношений. Если тождество является дробью, обязательно следует проверить условие неравенства знаменателя нулевой величине. Для этой цели следует решить соответствующее уравнение, вычислив его корни. Последние должны привести к пустому множеству, т. к. на 0 делить нельзя. Вот именно их и необходимо исключить, записав условие, т. е. t!=-9.

Таким образом, для грамотной оптимизации математических выражений необходимо пользоваться рекомендациями специалистов, правилами и методиками, поскольку их несоблюдение могут существенно повлиять на результаты вычислений.