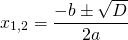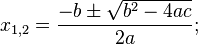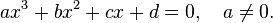Как решить уравнение в си шарп (8 видео)

Программирование на C, C# и Java

Содержание

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Решение квадратного уравнения на С# в Windows Forms.
Решение квадратного уравнения
Поиск по сайту
Решение квадратных уравнений
Решение кубических уравнений
Решение биквадратных уравнений
📺 Видео

Видео:ОПЕРАТОРЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ЧИСЛАМИ В C# | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | Урок # 8Скачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Решение квадратного уравнения на C# для консоли Windows в Visual Studio 2022Скачать

Решение квадратного уравнения на С# в Windows Forms.

Сегодня мы напишем программу, которая выведет нам решение квадратного уравнения на С#. Сделаем мы всё это в Windows Forms. В программе мы найдём дискриминант и оба корня.

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

Видео:Решение уравнений (метод дихотомии) на C#Скачать

Решение квадратного уравнения

Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.

a, b, c — действительные числа, a ≠ 0.

Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.

D = b 2 — 4⋅a⋅c;

если D 0, то уравнение имеет два действительных корня:
- x₁ = (-b + √D) / (2⋅a);
- x₂ = (-b + √D) / (2⋅a).

Видео:Научиться программировать - C# - "решение квадратного уравнения", разбор задачи (часть 1)Скачать

Поиск по сайту

Выражение вида f(x)=0 называется уравнением. Число х называется корнем уравнения, если при его подстановке уравнение обращается в верное равенство. В статье рассмотрим методы решения уравнений — как точных, так и численных (приближенных).

Видео:Решение квадратного уравнения на C# для Windows Forms в Visual Studio 2022Скачать

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

Классическая формула для нахождения его корней (действительных и комплексных):

где выражение D = b 2 − 4ac называется дискриминантом уравнения, от его значения зависит количество и характер решений:

Если D>0, то корней уравнения будет два и оба они будут действительными числами;
Если D=0, то будет лишь один дейсвительный корень уравнения;
Если D 2 +10x+200=0; данное уравнение не имеет действительных корней, но имеет пару сопряженных комплексных корней: x₁ = -1-6,2449979983984i, x₂ = -1+6,2449979983984i;
x 2 -8x+16=0; данное уравнение имеет один двукратный корень x₁=x₂=4;
x 2 -5x+6=0; данное уравнение имеет два различных корня x₁=2, x₂=3.

Напишем программу для решения этих уравнений:

На выходе получим:

5x^2 — 10x + 200 = 0
x0 = (-1, -6,2449979983984)
x1 = (-1, 6,2449979983984)

x^2 — 8x + 16 = 0
x0 = (4, 0)
x1 = (4, 0)

x^2 — 5x + 6 = 0
x0 = (3, 0)
x1 = (2, 0)

Воспользуемся WolframAlpha для проверки значений:

Видео:Задача 411. Квадратное уравнение. acmp.ru C++Скачать

Решение кубических уравнений

Кубическим уравнением называется уравнение третьего порядка, которое имеет вид

Кубическое уравнение всегда имеет 3 корня, которые могут быть как вещественными, так и комплексными. Для решения кубических уравнений используется метод Виета-Кардано.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета), о которых мы поговорим дальше.

Рассмотрим в качестве примера следующие кубические уравнения:

x^3 — 6x^2 + 11x — 6 = 0
x^3 — 6x^2 + 11x + 6 = 0

Напишем программу для решения кубических уравнений с помощью метода Виета-Кардано:

Напишем программу для тестирования метода:

x^3 — 6x^2 + 11x — 6 = 0
x0 = (1, 0)
x1 = (3, 0)
x2 = (2, 0)

x^3 — 6x^2 + 11x + 6 = 0
x0 = (-0,434841368216901, 0)
x1 = (3,21742068410845, 1,85643189109788)
x2 = (3,21742068410845, -1,85643189109788)

Решим эти же уравнения с помощью WolframAlpha.

Видео:Программа для решения квадратных уравнений на С++Скачать

Решение биквадратных уравнений

Биквадратное уравнение — уравнение четвёртой степени вида

где a,b,c — заданные комплексные числа и a != 0. Подстановкой y = x 2 сводится к квадратному уравнению относительно y. Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Рассмотрим в качестве примера кубические уравнения:

5x^4 — 10x^2 + 200 = 0
x^4 — 8x^2 + 16 = 0
x^4 — 5x^2 + 6 = 0

Таким образом немного модифицируем первую функцию для решения биквадратных уравнений:

Напшем программу для тестирования метода:

На выходе получим такие результаты:

5x^4 — 10x^2 + 200 = 0
x0 = (1,63164875514566, -1,91370783040891)
x1 = (-1,63164875514566, 1,91370783040891)
x2 = (1,63164875514566, 1,91370783040891)
x3 = (-1,63164875514566, -1,91370783040891)

x^4 — 8x^2 + 16 = 0
x0 = (2, 0)
x1 = (-2, 0)
x2 = (2, 0)
x3 = (-2, 0)

x^4 — 5x^2 + 6 = 0
x0 = (1,73205080756888, 0)
x1 = (-1,73205080756888, 0)
x2 = (1,4142135623731, 0)
x3 = (-1,4142135623731, 0)

По ссылкам раз, два, три можно убедиться в правильности решений.