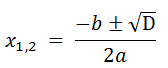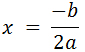Как решить уравнение в джава

Статья посвящена реализации алгоритма Гаусса для решения системы линейных алгебраических уравнений на языке Java.

Видео:Уроки Java для начинающих | #6 - Математические операцииСкачать

Теоретические сведения

Рассмотрим математическую теорию. Система линейных уравнений может иметь одно решение, бесконечно много решений или же быть несовместной (не иметь решений). Не все методы решения СЛАУ могут справится с вторым случаем, когда система имеет бесконечно много решений. Например, метод Крамера и матричный метод не применимы, но метод Гаусса вполне можно использовать.

Алгоритм можно условно разделить на два этапа:

• Прямой ход
• Обратный ход

В первом этапе образуются нули ниже или выше главной диагонали, за счет использования элементарных преобразований матрицы. На втором этапе находят неизвестные начиная с конца. Подробную теорию можно посмотреть по ссылке: метод Гаусса, поэтому с теорией пожалуй все. Перейдем к реализации.

Видео:Java - Структура - ДискриминантСкачать

Реализация

Начнем с постановки задачи:

• нам нужно создать программу, реализующую систему линейных уравнений в виде некоторой структуры данных, используя приемы обобщенного программирования. Система должна содержать коэффициенты производного типа от класса Number (т.е. Float, Integer, Double и т.д.)
• Запрограммировать алгоритм, который получив на вход структуру данных системы образует нули ниже главной диагонали

Начнем с написания интерфейса, который должно реализовывать каждое уравнение:

Здесь все должно быть ясно, N некоторый наследник Number‘а, T — некоторый тип, реализующий данный интерфейс (рекурсивные дженерики). Метод addEquation(T item) позволяет прибавить каждый элемент уравнения item к каждому своему элементу. Остальные методы работают аналогично.

Теперь рассмотрим класс системы уравнений. Как видно в листинге ниже, он дженеризирован так же, как и интерфейс Gauss и содержит методы для удобного доступа к приватному списку содержащих в себе уравнений.

Теперь можно приступать к реализации «частного случая» структуры уравнения. Создадим класс MyEquation, реализующий наш интерфейс. Пусть наследником Number‘а будет сверхточный класс Float (на практике лучше брать Double). Обратите внимание, что в методе addEquation(MyEquation item) используется объект класса ListIterator, позволяющий изменять элементы перебираемого списка.

Теперь имеем полноценную структуру данных, реализующую систему уравнений. Составим алгоритм который будет принимать некоторый объект, реализующий интерфейс Gauss, затем вызывая нужные методы приведет матрицу к нужному виду.

Алгоритм простой, найти нужный коэффициент, домножить на него i-ю строку (i=0..n-1), и прибавить ее к j-й строке (j=i..n). Заметьте, алгоритм не знает как именно реализуются методы findCoefficient, mul и addEquation, это придает коду бОльшую гибкость, т.к. при потребности изменить способы манипуляции уравнениями (строками), будут изменены только реализации трех вышеупомянутых методов, а главный алгоритм останется нетронутым.

Почти все. Осталось запустить это все в методе main:

Запустим это чудо, что бы проверить корректность работы…

Это все. Исходники можно скачать на github’е.

Видео:Java - урок 5.4 (Практика - решаем квадратное уравнение)Скачать

Вывод

Метод Гаусса не очень поддается обобщенному программированию (как видите обратный ход выполнен отдельно), однако вышла своеобразная реализация которая, надеюсь, поможет кому то лучше разобраться в искусстве использования интерфейсов и дженериков.

Видео:Java - Математические функцииСкачать

Программирование на C, C# и Java

Видео:#1 Java с нуля: находим наименьшее из 3 чисел JAVA |Задачи по программированию| JAVA базовые задачиСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:#29 Квадратное уравнение Решение задачи на языке JavaScript, Уроки по JavaScriptСкачать

Решение квадратного уравнения на Java

В этой статье рассмотрим алгоритм решения квадратного уравнения и реализуем его на языке программирования Java.

Пусть нам требуется решить уравнение вида: 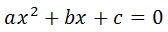. Будем решать его через дискриминант. Для получения корней уравнения необходимо выполнить следующий алгоритм:

Вычислим дискриминант по формуле: .

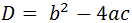ЕСЛИ дискриминант больше нуля, то вычислим корни уравнения x1 и x2 по формуле:

ИНАЧЕ ЕСЛИ дискриминант равен нулю, значит уравнение имеет единственный корень. Вычислим его по формуле:

ИНАЧЕ (то есть дискриминант меньше нуля) уравнение не имеет действительных корней.

Реализуем этот алгоритм на языке программирования Java.

Приступим к написанию кода программы. В начале импортируем класс Scanner, необходимый для ввода данных:

Видео:Разбор и вычисление арифметических выражений на JavaСкачать

Решение квадратного уравнения

В этой статье мы рассмотрим алгоритм решения квадратного уравнение на Java.

Видео:Математика это не ИсламСкачать

Что такое квадратное уравнение

Квадратно уравнение – это уравнение вида:

(1)

Для вычисления значения x мы сначала вычислим дискриминант по формуле:

(2)

Далее, если значение дискриминанта больше нуля, вычислим корни уравнения по формулам:

(3)

Иначе, если дискриминант равен нулю, единственное значение x вычислим по формуле:

(4)

Иначе, если дискриминант меньше нуля, данное уравнение не имеет решения.

Видео:Java. Многопоточность. Как устроить Deadlock.Скачать

Реализация алгоритма решения квадратного уравнения

Вначале вычитаем исходные данные a, b и c:

Затем вычислим дискриминант:

На основании значения дискриминанта вычислим корни уравнения, если таковые имеются:

Видео:#4 Арифметические операции | Java для начинающихСкачать

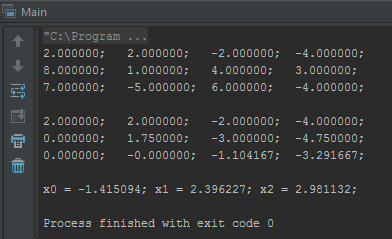
Проверка

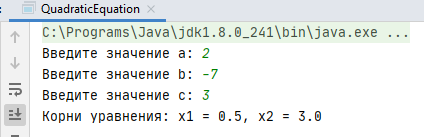
Теперь проверим программу в действии. Для следующих входных данных программа должна выдать такой результат:

(5)

Результат работы программы:

Видео:Уроки Java с нуля / #5 – Данные от пользователя. Математические действияСкачать

Исходный код

Полный исходный код программы:

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Заключение

Мы реализовали программу для решения квадратного уравнения. Вводные данные считываются с помощью Scanner.

🎥 Видео

Как выучить Java? Самый аху#### способ!Скачать

Как решать неполное квадратное уравнение? 😎Скачать

Java урок - 9.1 Рекурсия. Задача суммы с 1 до nСкачать

Уроки Java для начинающих | #4 - ПеременныеСкачать

Java урок - 8.1.2 Класс Math и методы округленияСкачать