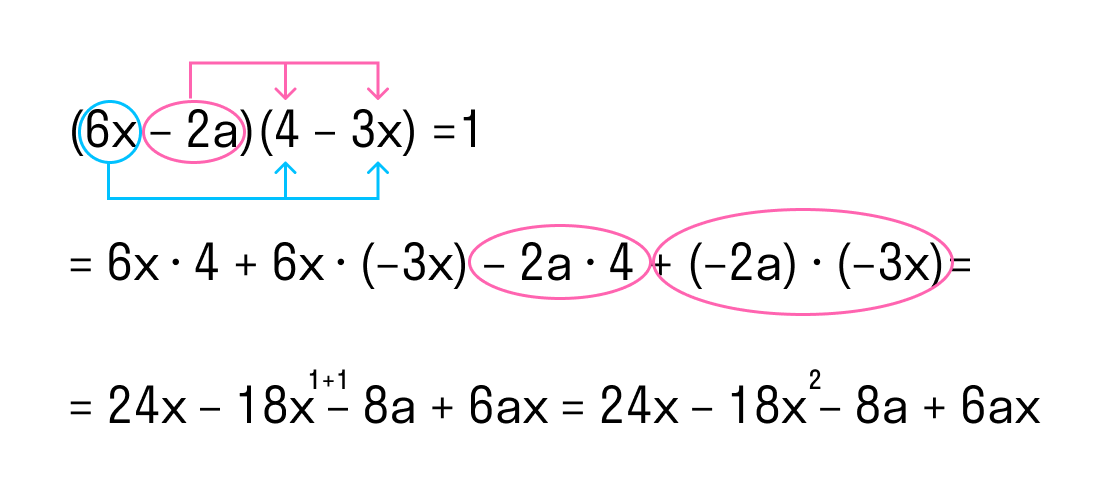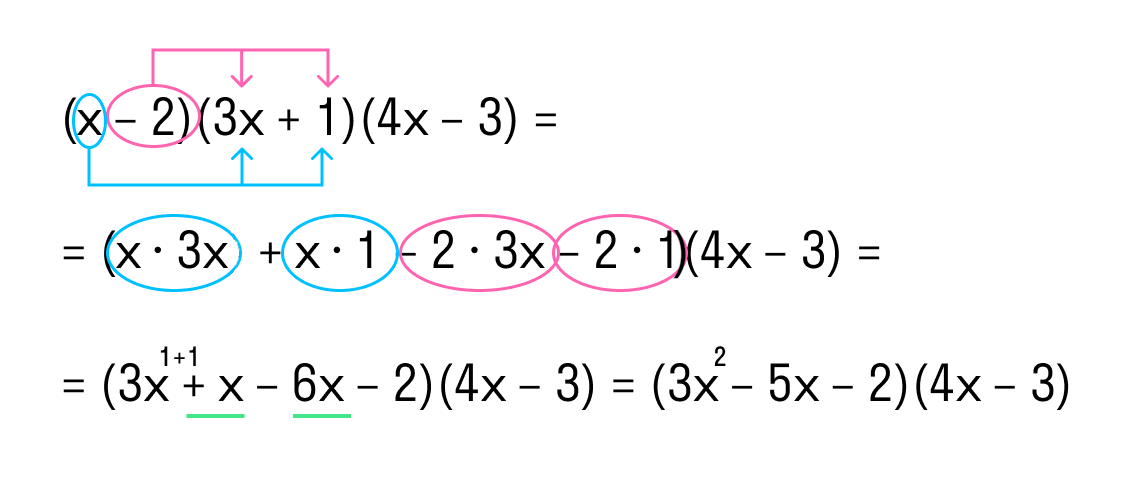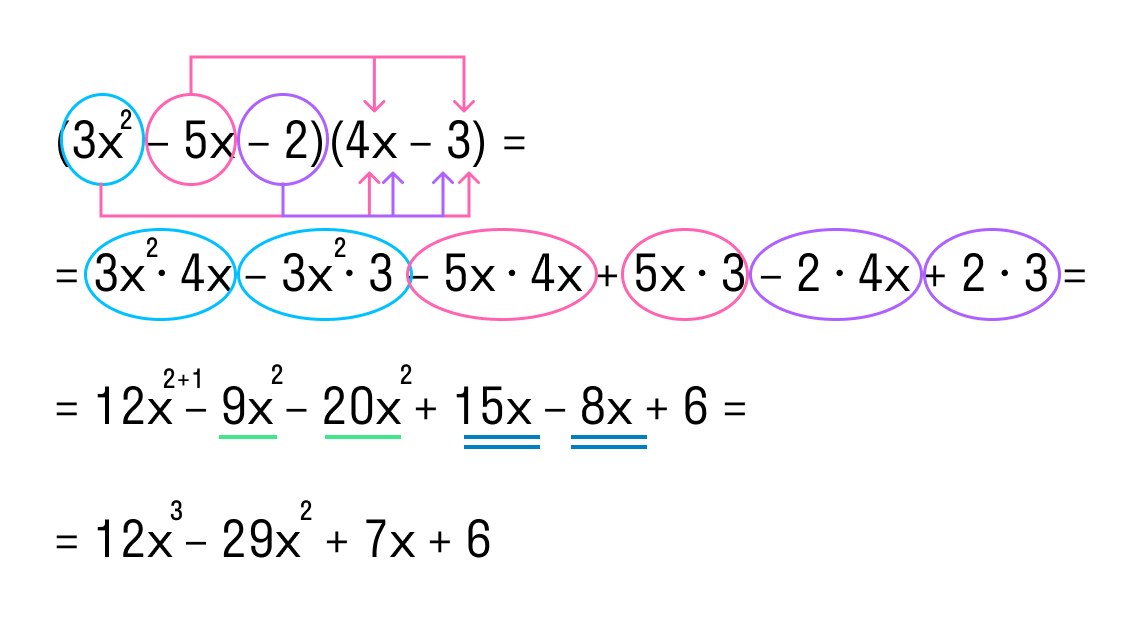Как решить уравнение умножение многочленов (6 видео)

Умножение многочлена на многочлен

О чем эта статья:

Содержание

Определение многочлена
Правило умножения многочлена на многочлен
Примеры умножения многочлена на многочлен
Умножение многочлена на многочлен
Умножение многочлена на многочлен: правило, примеры
Правило умножения многочлена на многочлен
Примеры умножения многочлена на многочлен
📺 Видео

Видео:7 класс, 23 урок, Умножение многочлена на многочленСкачать

Определение многочлена

Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.

Одночлен — это произведение чисел, переменных и степеней.

Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.

Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.

Как привести многочлен к стандартному виду:

Привести к стандартному виду все одночлены, которые входят в многочлен.
Привести подобные члены.

Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:

(a + b) * (c + d) = ac + ad + bc + bd.

Правило умножения двучлена на трехчлен:

(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.

Правило перемножения трехчленов:

(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.

Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.

Видео:7 класс// АЛГЕБРА // Умножение одночлена на многочлен, решение уравненийСкачать

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
Сначала составим их произведение: (a + b)(c + d).
Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
Проведем обратную замену x на (c + d):
a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd.
Как изменилось произведение исходных многочленов:
(a + b)(c + d) = ac + ad + bc + bd.
Как раз так и выглядит формула умножения многочлена на многочлен.

Правило умножения многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.

Алгоритм умножения многочлена на многочлен:

Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена. И так далее.
Сложить полученные произведения.
Преобразовать полученную сумму в многочлен стандартного вида.

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.

Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

Умножим первый многочлен на второй. Результат запишем в скобках.
Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Видео:Произведение многочленов. 7 класс.Скачать

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.

Запишем произведение: (2 − 3x)(x 2 − 7x + 1).

Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x 2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x 2 , 2(−7x) и 2*1.

Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx 2 , −3x(−7x) и −3x*1.

Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1 = 2x 2 − 14 x + 2 − 3x 3 + 21x 2 − 3x = (2x 2 + 21x 2 ) + (−14x − 3x) + 2 − 3x 3 = 23x 2 − 17x + 2 − 3x 3 .

Получается, что (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Ответ: (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.

Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.

Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Видео:7 класс// АЛГЕБРА // Умножение многочленов. Решение уравненийСкачать

Умножение многочлена на многочлен

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы вспомним все, что уже выучили про умножение многочленов, подведем некоторый итог и сформулируем общее правило. После этого выполним ряд примеров для закрепления техники умножения многочленов.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений».

Видео:Многочлены. 7 класс.Скачать

Умножение многочлена на многочлен: правило, примеры

Одним из действий с многочленами является умножение многочлена на многочлен. В данной статье рассмотрим правило такого умножения и применим его при решении задач.

Видео:Умножение многочлена на многочлен. Алгебра, 7 классСкачать

Правило умножения многочлена на многочлен

Зададим два многочлена a + b и c + d и выполним их умножение.

В первую очередь запишем произведение исходных многочленов: поставим между ними знак умножения, предварительно заключив многочлены в скобки. Получим: ( a + b ) · ( c + d ) . Теперь обозначим множитель ( c + d ) как x , тогда выражение получит вид: ( a + b ) · x , что по сути является произведением многочлена и одночлена. Осуществим умножение: ( a + b ) · x = a · x + b · x , а затем обратно заменим х на ( c + d ) : a · ( c + d ) + b · ( c + d ) . И вновь применив правило умножения многочлена на одночлен, преобразуем выражение в: a · c + a · d + b · c + b · d . Резюмируя: произведению заданных многочленов a + b и c + d соответствует равенство ( a + b ) · ( c + d ) = a · c + a · d + b · c + b · d .

Рассуждения, которые мы привели выше, дают возможность сделать важные выводы:

Результат умножения многочлена на многочлен — многочлен. Данное утверждение справедливо для любых перемножаемых многочленов.
Произведение многочленов есть сумма произведений каждого члена одного многочлена на каждый член другого. Откуда можно сделать заключение, что при умножении многочленов, содержащих m и n членов соответственно, указанная сумма произведений членов состоит из m · n слагаемых.

Теперь можем сформулировать правило умножения многочленов:

Для осуществления умножения многочлена на многочлен, необходимо каждый член одного многочлена умножить на каждый член другого многочлена и найти сумму полученных произведений.

Видео:7 класс, 22 урок, Умножение многочлена на одночленСкачать

Примеры умножения многочлена на многочлен

В практическом решении задач нахождение произведения многочленов раскладывается на несколько последовательных действий:

запись произведения умножаемых многочленов (многочлены заключаются в скобки и между ними записывается знак умножения);
выстраивание суммы произведений каждого члена первого многочлена на каждый член второго. С этой целью первый член первого многочлена умножается на каждый член второго многочлена, затем второй член первого многочлена перемножается с каждым членом второго многочлена и так далее;
если это возможно, полученная сумма записывается в виде многочлена стандартного вида.

Пример 1

Заданы многочлены: 2 − 3 · x и x 2 − 7 · x + 1 . Необходимо найти их произведение.

Решение

Запишем произведение исходных многочленов. Получим: ( 2 − 3 · x ) · ( x 2 − 7 · x + 1 ) .

Следующим шагом составим сумму произведений каждого члена многочлена 2 − 3 · x на каждый член многочлена x 2 − 7 · x + 1 . Рассмотрим подробно: умножаем первый член первого многочлена (число 2 ) на каждый член второго многочлена, получим: 2 · x 2 , 2 · ( − 7 · x ) и 2 · 1 . Затем умножаем второй член первого многочлена на каждый член второго многочлена и получаем: − 3 · x · x 2 , − 3 · x · ( − 7 · x ) и − 3 · x · 1 . Все полученные выражения собираем в сумму: 2 · x 2 + 2 · ( − 7 · x ) + 2 · 1 − 3 · x · x 2 − 3 · x · ( − 7 · x ) − 3 · x · 1 .

Проверим, не пропустили ли мы произведение каких-либо членов: для этого пересчитаем количество членов в записанной сумме, получим 6 . Это верно, поскольку исходные многочлены состоят из 2 и 3 членов, что в общем дает 6 .

Последним действием преобразуем записанную сумму в многочлен стандартного вида: 2 · x 2 + 2 · ( − 7 · x ) + 2 · 1 − 3 · x · x 2 − 3 · x · ( − 7 · x ) − 3 · x · 1 = = 2 · x 2 − 14 · x + 2 − 3 · x 3 + 21 · x 2 − 3 · x = = ( 2 · x 2 + 21 · x 2 ) + ( − 14 · x − 3 · x ) + 2 − 3 · x 3 = 23 · x 2 − 17 · x + 2 − 3 · x 3

Кратко без пояснений решение будет выглядеть так:

( 2 − 3 · x ) · ( x 2 − 7 · x + 1 ) = 2 · x 2 + 2 · ( − 7 · x ) + 2 · 1 − 3 · x · x 2 − 3 · x · ( − 7 · x ) − 3 · x · 1 = = 2 · x 2 − 14 · x + 2 − 3 · x 3 + 21 · x 2 − 3 · x = = ( 2 · x 2 + 21 · x 2 ) + ( − 14 · x − 3 · x ) + 2 − 3 · x 3 = 23 · x 2 − 17 · x + 2 − 3 · x 3

Ответ: ( 2 − 3 · x ) · ( x 2 − 7 · x + 1 ) = 23 · x 2 − 17 · x + 2 − 3 · x 3 .

Уточним, что, когда исходные многочлены заданы в нестандартном виде, перед тем, как найти их произведение, желательно привести их к стандартному виду. Результат, конечно, будет тот же, но решение станет удобнее и короче.

Заданы многочлены 1 7 · x 2 · ( — 3 ) · y + 3 · x — 2 7 · x · y · x и x · y − 1 . Необходимо найти их произведение.

Решение

Один из заданных многочленов записан в нестандартном виде. Исправим это, приведя его к стандартному виду:

1 7 · x 2 · ( — 3 ) · y + 3 · x — 2 7 · x · y · x = — 3 7 · x 2 + 3 · x — 2 7 · x 2 · y = = — 3 7 · x 2 · y — 2 7 · x 2 · y + 3 · x = — 5 7 · x 2 · y + 3 · x

Теперь найдем искомое произведение:

— 5 7 · x 2 · y + 3 · x · x · y — 1 = = — 5 7 · x 2 · y · x · y — 5 7 · x 2 · y · ( — 1 ) + 3 · x · x · y + 3 · x · ( — 1 ) = = — 5 7 · x 3 · y 2 + 5 7 · x 2 · y + 3 · x 2 · y — 3 · x = — 5 7 · x 3 · y 2 + 3 5 7 · x 2 · y — 3 · x

Ответ: — 5 7 · x 2 · y + 3 · x · x · y — 1 = — 5 7 · x 3 · y 2 + 3 5 7 · x 2 · y — 3 · x

Напоследок проясним ситуацию, в которой есть необходимость перемножить три и более многочленов. В этом случае нахождение произведения сводится к последовательному перемножению многочленов по два: т.е. сначала перемножаются первые два многочлена; полученный результат умножается на третий многочлен; итог этого умножения – на четвертый многочлен и так далее.

Заданы многочлены: x 2 + x · y − 1 , x + y и 2 · y − 3 . Необходимо найти их произведение.

Решение

Сделаем запись произведения: ( x 2 + x · y − 1 ) · ( x + y ) · ( 2 · y − 3 ) .

Перемножим первые два многочлена, получим: ( x 2 + x · y − 1 ) · ( x + y ) = x 2 · x + x 2 · y + x · y · x + x · y · y − 1 · x − 1 · y = = x 3 + 2 · x 2 · y + x · y 2 − x − y .

Первоначальная запись произведения принимает вид: ( x 2 + x · y − 1 ) · ( x + y ) · ( 2 · y − 3 ) = ( x 3 + 2 · x 2 · y + x · y 2 − x − y ) · ( 2 · y − 3 ) .

Найдем результат этого умножения:

( x 3 + 2 · x 2 · y + x · y 2 − x − y ) · ( 2 · y − 3 ) = = x 3 · 2 · y + x 3 · ( − 3 ) + 2 · x 2 · y · 2 · y + 2 · x 2 · y · ( − 3 ) + x · y 2 · 2 · y + + x · y 2 · ( − 3 ) − x · 2 · y − x · ( − 3 ) − y · 2 · y − y · ( − 3 ) = = 2 · x 3 · y − 3 · x 3 + 4 · x 2 · y 2 − 6 · x 2 · y + 2 · x · y 3 — − 3 · x · y 2 − 2 · x · y + 3 · x − 2 · y 2 + 3 · y

Ответ:

( x 2 + x · y − 1 ) · ( x + y ) · ( 2 · y − 3 ) = 2 · x 3 · y − 3 · x 3 + 4 · x 2 · y 2 − 6 · x 2 · y + + 2 · x · y 3 − 3 · x · y 2 − 2 · x · y + 3 · x − 2 · y 2 + 3 · y