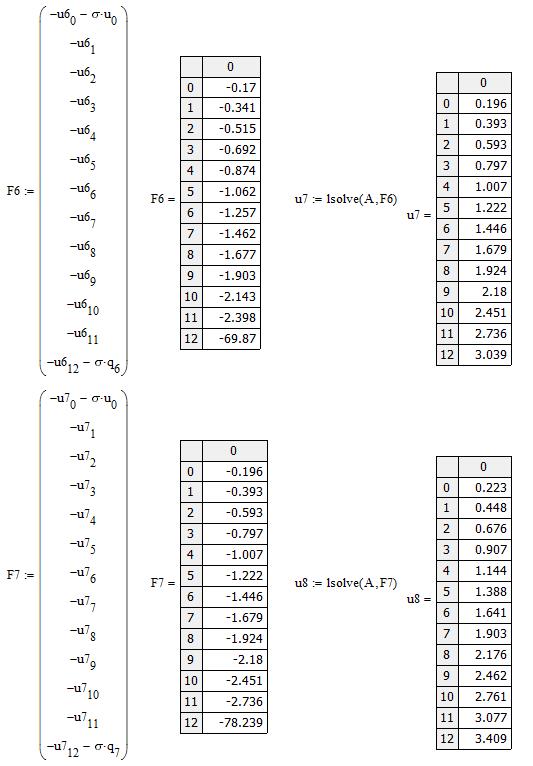
Как решить уравнение теплопроводности в маткад (3 видео)

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПАКЕТЕ МАТЕМАТИЧЕСКИХ РАСЧЕТОВ MATHCAD

Введением конечно-разностных соотношений в уравнение теплопроводности – дифференциальное уравнение второго порядка в частных производных – отыскание решения уравнения свелось к определению решений систем линейных алгебраических уравнений относительно значений температуры в точках сетки. Эти системы могут решаться любым из методов решения систем линейных алгебраических уравнений. В пакете MathCAD существует функция решения систем линейных алгебраических уравнений методом Гаусса lsolve. Воспользуемся ею для получения решения уравнения теплопроводности (1.1) с начальным (1.11) и граничными (1.12) условиями. Аргументами функции lsolve являются матрица коэффициентов перед неизвестными и столбец свободных членов системы. В данном случае предстоит многократное решение системы с одинаковой матрицей коэффициентов. Изменяются столбцы свободных членов.

Начиная решение, введем исходные данные и вычислим значения температуры на нулевом временном слое по начальным условиям (1.11). Далее зададим матрицу коэффициентов системы — матрицу А и столбец свободных членов (1.18) (рис.3.1). Находим решение системы, т.е. температуру на первом временном слое u1, и показываем результат вычислений (рис.3.2). Определена температура для внутренних узлов сетки. Для того чтобы найти температуру на втором временном слое, нужно решить систему с измененным столбцом свободных членов. Для получения решения на втором временном слое нужно пересчитать свободный столбец системы и снова ее решить. Особенностью вычисления в пакете MathCAD является то, что индексы у векторов отсчитываются от нуля, поэтому появляется несоответствие в записи формул. Решение для второго слоя u2 приведено на рис. 3.3.

Рис. 3.1. Подготовка данных для решения уравнения теплопроводности на первом временном слое

Рис. 3.2. Решение уравнения теплопроводности на первом временном слое

Рис. 3.3. Решение уравнения теплопроводности на втором временном слое

Рис. 3.4. Полное решение в MathCAD

Повторяя вычисления столбца свободных членов и решения системы еще десять раз, получим вектора u1, u2, u3,…, u15, содержащие значения температуры во внутренних точках сетки. Полное решение представлено на рис. 3.4. Графическое полного решения можно увидеть на рис. 3.7.

Далее предстоит собрать в одну матрицу начальные значения, краевые и вычисленные во внутренних узлах.

Рис. 3.5. Формирование матрицы с результатами

Рис. 3.6. Результат решения уравнения теплопроводности

Содержание

Как решить уравнение теплопроводности в маткад
Журнал «Психология образования в поликультурном пространстве»
Выпуск №14 Том №2 (II квартал 2011) 143 стр.
📺 Видео

Видео:Двумерное нестационарное уравнение теплопроводности в MatLab l 2D Heat transfer equation in MatLabСкачать

Как решить уравнение теплопроводности в маткад

11.1.2. Пример: уравнение диффузии тепла

На протяжении всей главы мы будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности.

Двумерное динамическое уравнение

Рассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:

Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции и часто, ради краткости, обозначают при помощи оператора Лапласа: Δ u ).

Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 11.1). Физический смысл коэффициента о, который, вообще говоря, может быть функцией как координат, так и самой температуры заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция φ (x,y,t,u) описывает приток тепла извне, т. е. источники тепла, которые также могут зависеть как от пространственных координат (что задает локализацию источников), так и от времени и от температуры и.

Рис. 11.1. Физическая модель, описываемая двумерным уравнением теплопроводности

Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия:

граничные условия, т. е. динамику функции u(x,y,t) и (или) ее производных на границах расчетной области;
начальное условие, т. е. функцию u (х, у, t) .

Если рассматривается не одно уравнение в частных производных, а система уравнений, то соответствующие начальные и граничные условия должны быть поставлены для каждой из неизвестных функций.

Стационарное двумерное уравнение

Частный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени, задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 11.2 в виде поверхности u(х,у) .

Рис. 11.2. Решение стационарного двумерного уравнения теплопроводности (см. листинг 11.7 ниже)

Как несложно сообразить, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения φ -φ /D ) следующим образом:

Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (11.2), принимающее вид Δu =0 , называют уравнением Лапласа.

Одномерное динамическое уравнение

Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 11.3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:

Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 11.4.

Начиная с версии Mathcad 11, для решения одномерных параболических и гиперболических уравнений можно применять встроенную функцию pdesolve .

Рис. 11.3. Физическая модель одномерного уравнения теплопроводности

Рис. 11.4. Решение одномерного уравнения теплопроводности (см. листинг 11.1 ниже)

Линейное и нелинейное уравнения

Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.

Линейная задача — если коэффициент диффузии о не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно).
Нелинейная задача — если уравнение имеет нелинейную зависимость от u(x,t) , т. е. или коэффициент диффузии зависит от и, и (или) источник тепла нелинейно зависит от и.

Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.

Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.

Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u ) и ф(и) . В частности, для металлов в большинстве случаев можно считать, что D=const , в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.

Обратное уравнение теплопроводности

Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:

Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами.

Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных уравнений (для этого достаточно в листинге 11.1 или 11.2 заменить значение коэффициента диффузии на отрицательное число, например, D=-1 ), то мы получим заведомо нефизичное решение. Оно показано на рис. 11.5 в виде профилей распределения температуры для нескольких последовательных моментов времени. Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма (как для ситуации, рассмотренной в разд. «Устойчивость»этой главы), а определяется спецификой самой задачи.

Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.

Рис. 11.5. Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры (см. листинг 11.2 ниже с параметром D=-1)

Видео:Нестационарное уравнение теплопроводности в матлабеl Time dependent heat transfer equation in MatLabСкачать

Журнал «Психология образования в поликультурном пространстве»

Видео:6-1. Уравнение теплопроводностиСкачать

Выпуск №14 Том №2 (II квартал 2011) 143 стр.

РЕШЕНИЕ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ С ПРИМЕНЕНИЕМ СИСТЕМЫ MATHCAD ПРИ ОБУЧЕНИИ УРАВНЕНИЯМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ СТУДЕНТОВ-ТЕПЛОЭНЕРГЕТИКОВ

задачи теплопроводности; аналитические методы решения; численные методы решения; система MathCAD; профессиональные компетенции

heat conduction problems; analytical methods; numerical methods for solving; the system MathCAD; professional competence

Современная ориентация инженерного образования на формирование общекультурных и профессиональных компетенций устанавливает приоритеты в профессиональной подготовке не только на получение новых математических знаний, но и на воспитание потребности и готовности к применению математических методов в профессиональной деятельности. В статье описываются методические особенности использования профессионально ориентированных задач на разных уровнях сложности с применением системы MathCAD при обучении уравнениям математической физики в рамках дисциплины «Математика» студентов направления «Теплоэнергетика и теплотехника».

Modern engineering education focused on the formation of common cultural and professional competence to establish priorities for professional training, not only for new mathematical knowledge, but also on education needs and readiness for the application of mathematical methods in their professional activities. This article describes the methodological features usage the career-oriented tasks at different levels of difficulty with the application of MathCAD in teaching the equations of mathematical physics in the framework of the discipline «Mathematics» students direction of «Heat power and heat engineering».

Исаченко, В. П. Теплопередача [Текст]: учеб. для вузов / В. П. Исаченко, В. А. Осипова, А. С. Сукомел. — М.: Энергоиздат, 1981. — 416 с.

Макаров, Е. Г. MathCAD [Текст]: учебный курс / Е. Г. Макаров. — СПб.: Питер, 2009. — 384 с.

Солодов, А. П. Электронный курс тепломассообмена в энергетических установках [Электронный ресурс]. Режим доступа: http://twt.mpei.ac.ru/solodov/HMT-eBook_2009/E_book_HMT.htm (обращение: 10.03.2011).

Тихонов, А. Н. Уравнения математической физики [Текст]: учеб. пособие для вузов / А. Н. Тихонов, А. А. Самарский. — М.: МГУ, 2004. — 799 с.

Цветков, Ф. Ф. Тепломассообмен [Текст]: учеб. пособие для вузов / Ф. Ф. Цветков, Б. А. Григорьев. — М.: Издательство МЭИ, 2005. — 550 с.