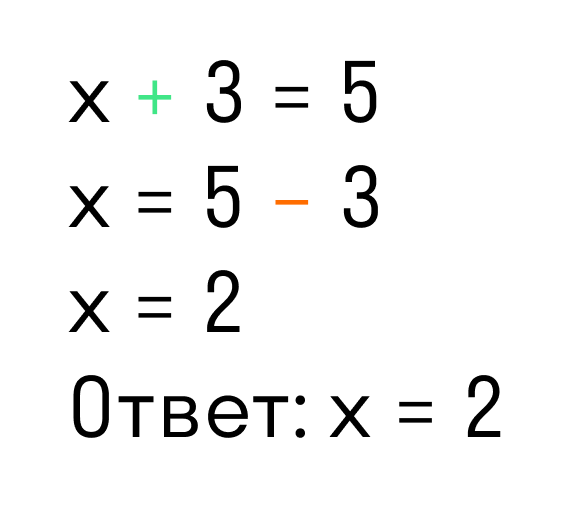Как решить уравнение со скобками 7 класс примеры и решения

О чем эта статья:

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

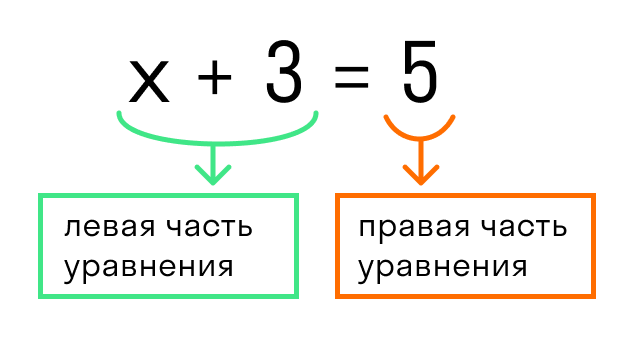
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

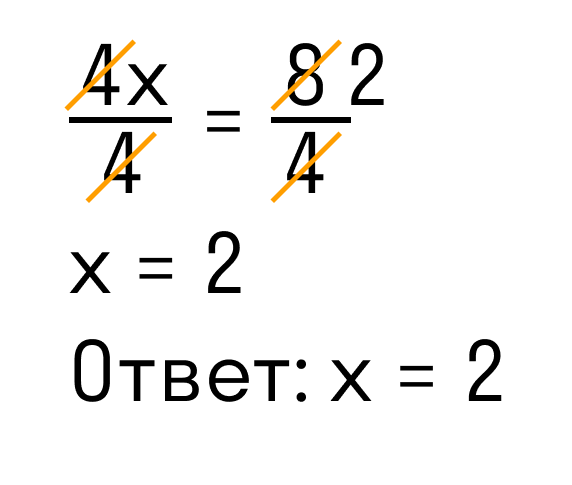
Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Учим алгебра 7 класс. Как решать уравнения алгебра 7 класс, примеры, дроби, функции, степени, модули

В 7 классе ученикам предстоит научиться решать уравнения, дроби, строить функции, разбираться в модулях. Для этого следует познакомиться с основными понятиями в темах, рассмотреть алгоритм решения и пошагово учиться находить ответы. Главное правило — начать с простых примеров, постепенно переходя на более сложные. Большинство задач можно решать несколькими методами (это касается и примеров), следует выбрать самый простой и удобный для себя.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Как решать уравнения алгебра 7 класс

Начнем с решения линейных уравнений (на рисунке показано, по какому принципу они устроены). Чтобы найти ответ в таких уравнениях, нужно совершать действия: раскрытие скобок, поиск подобных слагаемых, умножение/деление частей на одно и тоже число, перенос слагаемых из одной части уравнения в другую. Всё зависит от конкретного примера.

Рассмотрим несколько примеров пошагового решения линейных уравнений.

Пример 1.
6x + 24 = 0

Поскольку части уравнения (левая и правая) равны, то можно отнять из каждой одинаковое число. Равенство не изменится, а пример станет значительно проще. В представленном уравнении отняли 24 и слева, и справа. В левой части 24 сократилось, а в правой (0 — 24) получилось -24 (не забываем ставить знак минуса).

Получилось: 6x = -24. Теперь можем сократить 6 и -24 на число 6 (или рассуждаем так: чтобы найти множитель, нужно произведение разделить на другой множитель). В ответе будет -4. Не забудьте в самом конце подставить полученное число вместо х. Совпал ответ — значит, все правильно.

Можно рассуждать проще: чтобы упростить уравнение, нужно из левой части отправить в правую число 24, поменяв его знак. Равенство сохранится (на рисунке ниже).

Пример 2.
9 + 16x = 41 + 14x

Это уравнение более сложное. Здесь важно запомнить несколько моментов:

• числа без х переносятся в левую часть, а с х — в правую;
• при переносе знаки меняют.

Пример 3.
7(10 — 4x) + 5x = 12 — 3(5x + 2)

1. Раскрыть скобки, выполнив умножение: 7 умножаем на каждое число в скобках (в правой части -3 на каждое). При выполнении действия не забывайте сохранять знаки.
2. Записываем уравнение, получившееся после раскрытия скобок. Ещё раз сверяем знаки.
3. Числа с х отправляются в левую часть, без х — в правую. Знаки чисел, которые переходят в другую часть, меняем.
4. Подсчитываем результат с обеих сторон.
5. Делим -64 на -8 и получаем ответ. Не забываем, что минус на минус при делении и умножении дают плюс.

В рассмотренных уравнениях корень точно определён. Так получается не всегда.

Пример 4.

Обратите внимание, в ответе получилось 0x = 0. Это значит, что x может быть любым числом, потому что при умножение хоть какого числа на 0 получится 0.

В этом примере корней нет, так как любое число, которое умножают на 0, будет равно 0 (21 никак не получится).

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Как решать систему уравнений алгебра 7 класс

Системой называют несколько уравнений, в которых нужно найти такие значения неизвестных, чтобы равенство сохранилось. Разберемся на примерах, как выглядят системы и какие методы их решения существуют.

метод подстановки

Из самого названия следует, что алгоритм требует что-то подставлять. Ниже представлена система, где нужно найти значения x и y.

Суть метода подстановки: переменную в одном из уравнений выражают через другую переменную. Затем подставляют полученное выражение в другое уравнение.

Смотрим на систему. Видим, что удобнее будет выразить x во втором уравнении (так как он один). Выражаем путем переноса за знак «равно» 12y. Получилось: x = 11 — 12y (не забываем менять знак при переносе числа).

В первое уравнение вместо «x» записываем получившееся выражение. Меняем только x, остальное сохраняется в прежнем виде.

Далее преобразуем уравнение, в которое поместили выражение. Раскрываем скобки (перемножаем 5 на каждое значение). y оставляем в левой части, числа переносим в правую, знаки меняем. Таким образом нашли значение y (y = 1).

Теперь подставляем полученную единицу во второе уравнение (x = 11 — 12y).

Убедиться в правильном решение можно так: подставьте полученные значения в систему. Если равенства сохранятся, значит, решено верно.

метод сложения

Чтобы решить систему методом сложения, нужно из двух уравнений сделать одно. Просто складываем первое и второе. Здесь «y» просто сократились, и получилось простое уравнение. Как только нашли значение «х», нужно подставить его в любой пример (здесь поставили во второе уравнение). В ответе пишется так: (4; 3) — первым всегда пишется х, затем у.

графический метод

У нас есть система, где y = 5x и y = -2x + 7. Рассмотрим алгоритм решения системы уравнений:

1. Подбираем 2 числа для х. Мы взяли 0 и 1, подставляем в первое уравнение: y = 5 * 0 = 0; у = 5 * 1 = 5. Значит первая прямая имеет координаты: (0; 0) и (1; 5).
2. Для второго уравнения подбираем значения х. Взяли 3 и 2, подставляем и находим у: -2 * 3 + 7 = 1; -2 * 2 + 7 = 3. Значит прямая имеет координаты (3; 1) и (2; 3).
3. Отмечаем на графике соответствующие прямые, подписываем их название.
4. на месте пересечения получившихся прямых ставим точку — это будет решение.
5. Точка имеет координаты (1; 5).

На заметку! Старайтесь подбирать такие значения х, чтобы у был небольшим. Так отмечать будет проще.

Выбирайте самый удобный способ решения. Третий метод — графический, считают самым неточным.

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Как решать дроби 7 класс

Дроби можно разделить на 2 основных вида:

Они различаются в способе написания (смотрите рисунок ниже). В свою очередь и те, и другие делятся еще на несколько видов.

Для начала рассмотрим решение примеров с десятичными дробями.

Особое внимание при решении стоит уделить запятым. При сложении и вычитании запятые стоят строго друг под другом, при умножении это не имеет значения.

Примеры решения обыкновенных дробей.

• при сложении и вычитании нужно привести дроби к общему знаменателю, найти дополнительные множители. Так, для чисел 6 и 4 общим знаменателем стало число 24. Дополнительные множители считали так: 24 : 6 = 4 (для первой дроби) и 24 : 4 = 6 (для второй). Потом умножили доп. множители на числители и полученные числа сложили. Если в ответе получилась неправильная дробь, то выделяем целую часть, при необходимости сокращаем дроби.
• при умножении пишем дроби под одной чертой, сокращаем.
• при делении нужно вторую дробь перевернуть, поставить знак умножения и сократить дроби.

Если пример состоит из простой и десятичной дроби, то следует привести их к одному виду (к которому проще или удобнее считать).

Видео:Как решать уравнения с дробью? #shortsСкачать

Примеры 7 класс как решать

Теперь закрепим решение дробей на примерах.

Решение примера, представленного ниже:

1. Видим, что присутствует как обыкновенная дробь, так и десятичные. Нужно привести к одному виду. Так как десятичных больше, и превратить 1/4 в этот вид проще, то делим 1 на 4, а целую часть сохраняем. Вышло 5,25.
2. Далее умножаем — 3 на каждое число в скобках, внимательно следим за знаками.
3. Остается от 10,4 отнять 9,3. В итоге вышло 1,1.

Но можно было решить проще. Первое действие всегда в скобках. Поэтому от 5,25 отнимаем 2,15. Получится 3,1. Умножаем ее на 3 — вышло 9,3. И отнимаем: 10,4 — 9,3 = 1,1. Этот способ даже проще, потому что не нужно следить за знаками при раскрытии скобок.

Чтобы верно решить следующий пример, нужно:

• точно проставить порядок действий (умножение и деление делаем в первую очередь, затем складываем);
• Умножить десятичные дроби столбиком, не забыть поставить запятую;
• деление здесь простое: переставили запятую на один знак вправо, поделили, получили -2.
• сложили числа.

Видео:Алгебра 7 класс с нуля | Математика | УмскулСкачать

Как решать задачи алгебра 7 класс

Задачи решаются путем составления уравнений.

Другие примеры задач с подробными решениями в видео-материалах.

Видео:Вынесение общего множителя за скобки | Алгебра 7 классСкачать

Как решать функции алгебра 7 клас с

Функцией принято считать зависимость y от x. При этом x является переменной (или аргументом), а у — это значение функции (зависимая переменная).

• y(x) = 8x
• y(x) = −3x — 62
• y(x) = x−1 + 18

Чтобы найти значение у, которое бы соответствовало определенному значению х, нужно просто это значение х подставить в функцию.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Как решать степени алгебра 7 класс

Если требуется взять какое-либо число несколько раз, то проще записать его в степени. Например, нужно двойку взять три раза, т. е.: 2 * 2 * 2. Получается длинная запись. Поэтому придумали писать так: 2³ (читается: два в третьей степени).

Видео:Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать

Чтобы число возвести в степень (она указывается справа от числа вверху), нужно его умножать на самого себя столько раз, какая цифра указана. Рассмотрим подробнее на примерах.

Не всегда получается возвести число в степень «в уме». Иногда посчитать сложно. Например, возвести 6 в 5 степень, быстро получится не у каждого. Чтобы всякий раз не считать столбиком, лучше выучить основные степени. Они представлены в таблице.

При возведении любого числа в степень 1, получится это же число. Если возводить число в нулевую степень, в ответе будет 1.

Рассмотрим несколько примеров со степенями.

Отдельное внимание обращаем на возведение в степень отрицательного числа. Если такое число возводить в четную степень (2; 4; 6 и т.д.), то получится положительный ответ, если в нечетную, то ответ со знаком минус.

Видео:Сложение и вычитание многочленов. Алгебра, 7 классСкачать

Алгебра модули как решать

Модулем числа называют это же число, только без знака минус. Например: | − 9 | = 9. При этом если число изначально неотрицательное, то оно остается прежним.

Перейдем к простым примерам.

Логично предположить, что под модулем будет число 4. Также подойдет число -4, ведь из-под модуля все равно выйдет положительное. Так, корнями уравнения будут: x = 4 и x = − 4.

Из-под модуля не может выйти отрицательное число. Поэтому, если видим что-то похожее: Ι-8 + хΙ = -8, значит, корней не будет, так как уравнение заведомо нерешаемо.

Другие примеры описаны в видео.

Об Авторе

Смотрите также

Видео:Раскрытие скобок. 6 класс.Скачать

Сочинение рассуждение на тему патриотизм, патриотизм сочинение ЕГЭ: ложный и истинный патриотизм, народный патриотизм роман Война и мир, примеры сочинений

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Урок патриотизма в школе. Тема урока патриотизм: урок литературы патриотизм, патриотическое воспитание на уроках истории, урок мужества патриотизм. Дети герои Великой Отечественной войны Валя Котик, Валерий Волков, Марат Казей, Надя Богданова, Люся Герасименко, Вашкевич Лида, Валя Зенкина, Костя Кравчук, Вася Коробко, Витя Хоменко, Саша Ковалёв: краткая биография

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Современный сценарий выпускного в школе: сценарий выпускного современный прикольный веселый, красивые платья на выпускной 11 класс, современные песни текст на выпускной

2 комментария

Спасибо большое очень помогли.

Огромное спасибо!А то учитель неможет нормально тему объяснить

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Урок по алгебре в 7-м классе по теме: «Решение уравнений с применением приемов разложения многочлена на множители»

Разделы: Математика

Ребята, достаточно долго овладевая приёмами разложения многочлена на множители, подошли к моменту, когда необходимо систематизировать и обобщить изученные способы, попытаться сделать новые открытия и самое главное: найти интересное применение разнообразных приёмов разложения на множители к решению порой одинаковых по смыслу уравнений.

1. Что, значит, разложить многочлен на множители?

2. В каком случае произведение множителей равно 0?

3. Степень, какого числа равна нулю? 1??

4. Какие приёмы разложения на множители вам известны? (Вынесение общего множителя за скобки, группировка слагаемых с последующем вынесением общего множителя, с помощью формул сокращенного умножения).

5. Чему равны квадрат суммы, разности двух слагаемых?

6. Чему равна разность квадратов двух слагаемых?

На доске записаны уравнения:

По какому признаку можно разбить эти уравнения в группы? (Уравнения, содержащие многочлен второй степени. Уравнения, содержащие многочлен выше второй степени. Уравнение, содержащее многочлен второй степени, коэффициенты которого периодические дроби).

Нам предстоит решить эти уравнения, подбирая непохожие способы решения, несмотря порой на похожесть уравнений.

Предлагаю учащимся решить уравнение двумя способами. Вызываю к доске двух учеников.

Один ученик решает уравнение разбиением одночлена 6х на сумму двух одночленов, а другой – применением формулы сокращённого умножения – квадрата суммы:

Вопрос: Какой способ оказался более рациональным? (Конечно второй). Как его можно назвать?

(Выделение полного квадрата суммы)

Обсуждаем решение уравнения .

Можно ли решить уравнение, разбивая одно из слагаемых на два?

(да,)

А выделением полного квадрата суммы?

(затруднительно, так как, число 3 не является квадратом никакого рационального числа)

И всё-таки попробуем выделить полный квадрат суммы: дополните сумму первых двух слагаемых до квадрата суммы.

Как можно разложить многочлен в левой части уравнения на множители? (По формуле разности квадратов).

Сообразите, можно ли рассуждая аналогично решить уравнение ?

(Неудобное в данном случае число 5).

И все-таки, попробуем строго следовать формуле квадрата суммы при выделении полного квадрата:

Обратите внимание на коэффициенты уравнения . Какую закономерность можно заметить?

(Одинаково читаются слева направо)

Что происходит с показателями переменной x?

(Уменьшаются на один)

Выскажите предположение для многочлена в левой части уравнения.

(Многочлен х 4 +4х 3 +6х 2 +4х+1 есть (х+1) 4 ). Обоснуйте это.

(Построим треугольник Паскаля

14641 4-ая строка содержит коэффициенты возведения в 4-ую степень двучлена (х+1)

Итак, какой вид примет уравнение? Решите его устно.

Решите устно уравнение

Какими числами являются коэффициенты уравнения

(Периодическими десятичными дробями)

Обратите периодические дроби в обыкновенные и решите, получившееся уравнение.

(Правило обращения периодической десятичной дроби в обыкновенную: чтобы периодическую десятичную дробь обратить в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде и после девятки дописать столько нулей, сколько цифр между запятой и первым периодом)

(Подберите рациональный способ решения и найдите корни уравнения, х=1 или )

Вновь обратимся к уравнению . Решим это уравнение методом неопределённых коэффициентов:

Сравните значения найденных корней со значениями переменных b и d. (Они противоположны)

Найденные корни подтверждают мысль о том, что независимо от способа решения корни не меняются.

Чем уравнение похоже на предыдущее?

(Коэффициент при х 2 равен 1)

Попробуем решить это уравнение устно, не применяя ни один из рассмотренных приёмов, но

принимая во внимание некоторые рассуждения в предыдущем случае:

Запишите разложение многочлена в виде произведения двучленов:

Тогда, скажите чему, будут равны значения выражений и по аналогии с предыдущими рассуждениями?

( Легко догадаться, что или наоборот).

Сообразите, чему будут равны корни уравнения?

Устно решите уравнения:

1. С каким новым способом решения квадратных уравнений вы познакомились?

(Выделение полного квадрата суммы или разности)

2. Как вы думаете, почему этот способ не всегда удобен?

(Например, в уравнении 3х 2 -2х-1=0 3х 2 не является квадратом рационального выражения)

3. Какое открытие вы сделали, применяя метод неопределённых коэффициентов для

решения квадратных уравнений, если коэффициент при равен 1?

(Чтобы найти корни, надо сначала найти два таких числа в и с, чтобы их сумма была равна второму коэффициенту, а произведение – третьему слагаемому. А корни будут равны числам, противоположным числам .

В 8 классе вы познакомитесь с ещё одним способом решения квадратных уравнений – по формулам. Узнаете, кто такой Франсуа Виет и какое отношение он имеет к нашему открытию.

📸 Видео

АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 7 класс ПРИМЕРЫ формулы КАК РЕШАТЬ урок 1Скачать

Уравнения со скобками - 5 класс (примеры)Скачать