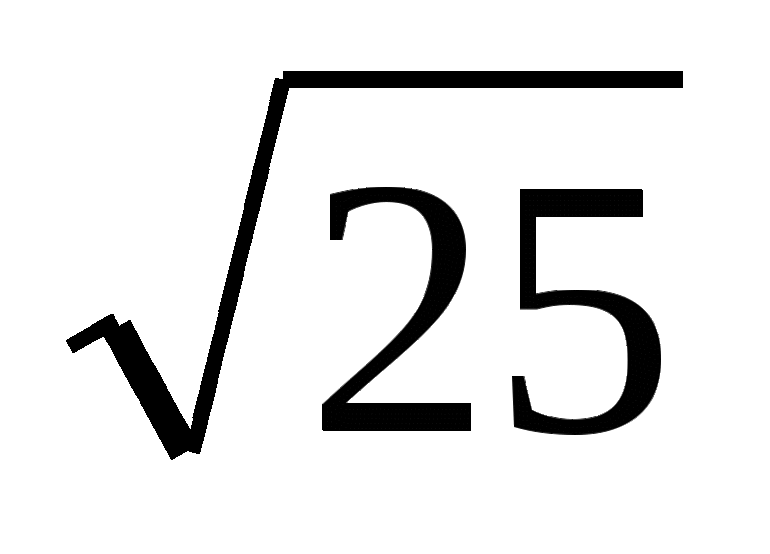Как решить уравнение с параметром и корнем

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Решение иррациональных уравнений и систем уравнений с параметром

Иррациональными уравнениями называются уравнения, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень. При этом, степень корня может быть произвольной.

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

В России появится перечень разрешённых электронных образовательных ресурсов

К 1 января в России появится перечень электронных ресурсов, разрешенных к использованию в школах. Об этом в интервью «Российской газете» рассказала глава Комитета Госдумы по просвещению Ольга Казакова.

Видео:1.10 решить уравнение с параметром под корнемСкачать

Госслужащих заставят сдавать экзамен по русскому языку

Чиновников скоро заставят сдавать экзамен на знание русского языка и умение говорить на нем правильно, красиво, без канцелярита. Об этом сообщила ректор Государственного института русского языка имени Пушкина, член Совета при президенте РФ по русскому языку Маргарита Русецкая.

Видео:Корни уравнения с параметромСкачать

Пробный вариант ЕГЭ-2022 по русскому языку

Соответствует демоверсии ЕГЭ-2022. Вариант составлен на основе заданий открытого банка ФИПИ.

Видео:Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Аналитический методСкачать

Различные методы решения иррациональных уравнений с параметрами

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Различные методы решения иррациональных уравнений

Методы решения иррациональных уравнений с параметрами.

Существует несколько способов решения иррациональных уравнений с параметрами.

Далее в работе различные способы решения иррациональных уравнений с параметрами будем разбирать на конкретных примерах.

х — = 1 (1)

Возведем в квадрат обе части иррационального уравнения с последующей проверкой полученных решений.

Перепишем исходное уравнение в виде:

= х – 1 (2)

При возведении в квадрат обеих частей исходного уравнения и проведения тождественных преобразований получим:

Особое значение: а = 0,5.

при а > 0,5 х_1,2 = 0,5 (1 ± );

Так как левая часть равенства отрицательна, то х₁ не удовлетворяет исходному уравнению.

Подставим х₂ в уравнение (2):

=

Проведя равносильные преобразования, получим:

Если , то можно возвести полученное равенство в квадрат:

Имеем истинное равенство при условии, что

Это условие выполняется, если а ≥1. Так как равенство истинно при а ≥1, а х₂ может быть корнем уравнения (1) при а > 0,5, следовательно, х₂ – корень уравнения при а ≥1.

;

;

;

;

;

Изобразим график:

;

Если , то нет решений;

Если , то

Если , то ;

Если , то 1 – решение.

= 2 x — 1

x ₁ =

x ₂ =

Рассмотрим функцию f ( x )=4 x ²-8 x +1- a

уравнение имеет 2корня.

уравнение имеет 1 корень.

D a a =3 или a -2 уравнение имеет 1 корень x = 1 или x = ;

Если -3 a X ₁= ;

X ₂= .

D /4 = 16 – 4(1 – а) = 16 – 4 + 4а

Если а > -3, то D > 0.

Система имеет два решения:

а > -3

Единственное решение, если

½ ( 2 — ) ½

½ ( 2 + ) ≥ ½

> 1

≥ -1

Если a a =3 или a -2 уравнение имеет 1 корень x = 1 или x = ;

Если -3 a X ₁= ;

X ₂= .

Краткое описание документа:

Методы решения иррациональных уравнений с параметрами.

Существует несколько способов решения иррациональных уравнений с параметрами.

Далее в работе различные способы решения иррациональных уравнений с параметрами будем разбирать на конкретных примерах.

Возведем в квадрат обе части иррационального уравнения с последующей проверкой полученных решений.

Перепишем исходное уравнение в виде:

При возведении в квадрат обеих частей исходного уравнения и проведения тождественных преобразований получим:

2 х2 – 2х + (1 — а) = 0, D = 2а – 1.

Особое значение: а = 0,5.

1. при а > 0,5 х1,2 = 0,5 (1 ± );

2. при а = 0,5 х = 0,5;

3. при а 1. при подстановке х = 0,5 в уравнение (2), равносильное исходному, получим неверное равенство. Значит, х=0,5 не является решением (2) и уравнения (1).

2. при подстановке х1 = 0,5 ( 1 ± ) в (2) получим:

-0,5 (1 + ) = – ( 0,5 ( 1 — ))2

Так как левая часть равенства отрицательна, то х1 не удовлетворяет исходному уравнению.

3. Подставим х2 в уравнение (2):

Проведя равносильные преобразования, получим:

Если , то можно возвести полученное равенство в квадрат:

Имеем истинное равенство при условии, что

Это условие выполняется, если а ≥1. Так как равенство истинно при а ≥1, а х2 может быть корнем уравнения (1) при а > 0,5, следовательно, х2 – корень уравнения при а ≥1.

· Если , то нет решений;

· Если , то 1 – решение.

Рассмотрим функцию f ( x )=4 x ²-8 x +1- a

уравнение имеет 2корня.

уравнение имеет 1 корень.

3. D уравнение не имеет корней.

· Если a =3 или a -2 уравнение имеет 1 корень x = 1 или x = ;

D /4 = 16 – 4(1 – а) = 16 – 4 + 4а

• Если а D • Если а = -3, то D = 0.

х1 = х2 = 4 / 4 = 1

• Если а > -3, то D > 0.

· Система имеет два решения:

· Единственное решение, если

· Если a =3 или a -2 уравнение имеет 1 корень x = 1 или x = ;

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Простое уравнение с параметром с корнями | Параметр 98 | mathus.ru #егэ2024Скачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 575 981 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 04.02.2015
• 1580
• 17

• 04.02.2015
• 1675
• 10

• 04.02.2015
• 14692
• 51

• 04.02.2015
• 52253
• 108

• 04.02.2015
• 1363
• 0

• 04.02.2015
• 766
• 3

• 04.02.2015
• 1735
• 10

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 04.02.2015 980
• DOCX 74.3 кбайт
• 5 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Синкина Ольга Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет
• Подписчики: 0
• Всего просмотров: 6673
• Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Сможешь решить иррациональное уравнение с параметром?Скачать

Уравнения с параметром — алгоритмы и примеры решения

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

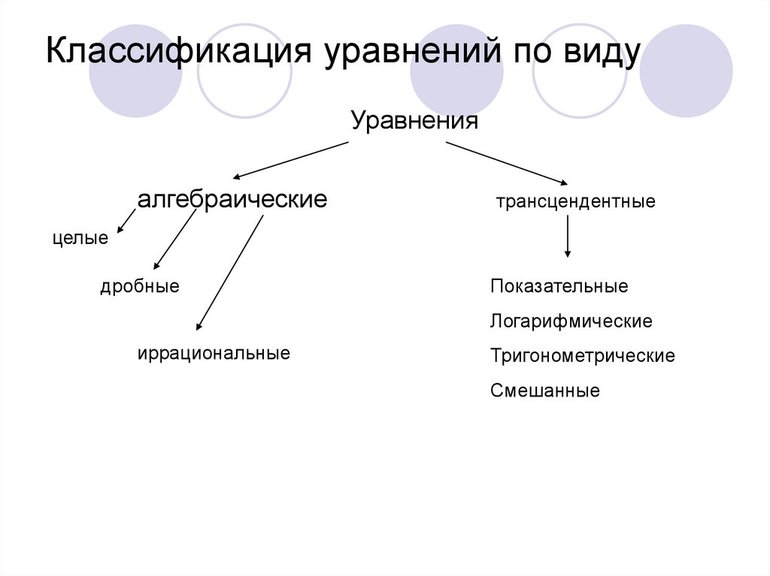
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Видео:Алгебра 8 класс (Урок№33 - Уравнения с параметром. Контрольный урок.)Скачать

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

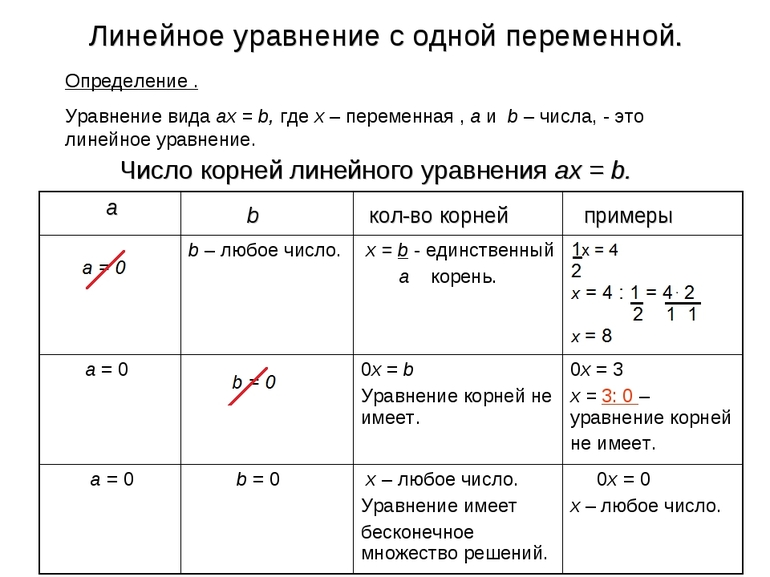
Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Видео:Реши любой параметр. Задача 18 Профильный ЕГЭСкачать

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: ^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

🌟 Видео

✓ Новые четыре способа решить параметр | ЕГЭ. Задание 17. Математика. Профиль | Борис ТрушинСкачать

9 класс. Алгебра. Уравнение с параметрами.Скачать

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Решаем квадратное уравнение с параметромСкачать

8 класс, 39 урок, Задачи с параметрамиСкачать

Сможешь решить уравнение с параметром?Скачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Сможешь решить уравнение с параметром? Из ЕГЭ 2019Скачать