Как решить уравнение с обратной заменой (6 видео)

Метод замены переменной

Содержание

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.
Примеры использования метода замены переменной
Биквадратное уравнение. Алгоритм решения и примеры.
Формула биквадратного уравнения:
Как решаются биквадратные уравнения?
Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.
Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.
📺 Видео

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение (x+frac) буквой (t).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно (t), после чего, сделав обратную замену, вычислим (x).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение (sin x) буквой (t).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Видео:Решение уравнения методом замены переменнойСкачать

Примеры использования метода замены переменной

Заметим, что (x^4=(x^2 )^2) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя (x^2) на (t).

Мы нашли чему равно (t), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: (±1); (±) (frac) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти (x), а не (t)! Поэтому возврат к (x) — строго обязателен!

Пример. Решить неравенство: (log^2_3⁡x-log_3⁡x-2>0)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Видео:решение уравнения с заменой переменнойСкачать

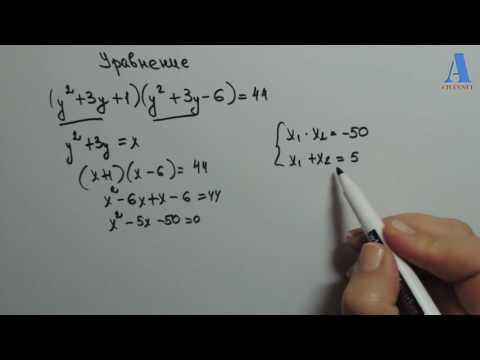
Биквадратное уравнение. Алгоритм решения и примеры.

Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Формула биквадратного уравнения:

Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.

ax 4 +bx 2 +c=0, где a≠0

Видео:Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

Как решаются биквадратные уравнения?

Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю

Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.

(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:

Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.

Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)

Возвращаемся в замену, подставим вместо переменной t полученное число:

Можно не во всех случаях делать замену. Рассмотрим пример.

Пример №3:
Решить биквадратное уравнение.

Выносим переменную x 2 за скобку,

Приравниваем каждый множитель к нулю

Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)

Пример №4:
Решите биквадратное уравнение.
(x^-16=0)

Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)

Ответ: решения нет.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:9 класс. Алгебра. Решение уравнений. Замена переменной.Скачать

Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.

Решение уравнений, приводящихся к квадратным. Биквадратные уравнения. Замена переменной в уравнениях. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Уравнения, приводящиеся к квадратным путем замены переменной. Квадратные уравнения. Алгебра 8 класс. Примеры с решением.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.

Биквадратные уравнения. Уравнения 4-й степени. Замена переменной в уравнениях. Решение уравнений, приводящихся к квадратным, путем замены переменной. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Алгебра 8 класс. Примеры с решением.

Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.

Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.

Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.

Пример 1: Решите уравнение методом замены переменной:

Если необходимо решить уравнение вида (x+A)(x+B)(x+C)(x+D) = m где А, В, С, D и m — некоторые константы, то группируем попарно скобки таким образом, чтобы была равна сумма констант, входящих в эти скобки.

Например, если А+D = В+C, то записываем: (x+A)(x+D)(x+B)(x+C) = m

Попарно раскрываем скобки: (x2+Ax+Dх + AD)(x2+Bx+Cх +DC) = m (x2+(A+D)х + AD)(x2+(B+C)х + DC) = m
Делаем замену x2+(A+D)х = t Получаем уравнение (t + AD)(t + DC) = m
После раскрытия скобок получим обычное квадратное уравнение.

Урок 5. Решение дробно-рациональных уравнений методом замены.

Решение дробно-рациональных уравнений методом замены. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Решение рационального уравнения заменой. Обратные числа. Какие числа называются взаимно обратными? Взаимно-обратные дроби. Как правильно сделать замену взаимно-обратных дробей. Примеры с решением. Задания с объяснением.

Урок 6. Решение дробно-рациональных уравнений методом замены переменной. Алгебра 8 класс.

Решение дробно-рациональных уравнений методом замены. Задания с *. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Как правильно возвести в квадрат при замене переменной. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.

Урок 7. Решение уравнений методом замены. Как понизить степень уравнения заменив переменную?

Решение дробно-рациональных уравнений методом замены. Как понизить степень уравнения заменив переменную? Задания с *. Алгебра 8 класс. Как сделать замену в рациональном уравнении? Уравнения 4-й степени. Понизить степень уравнения, сделав замену. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.

Урок 8. Замена переменной. Решение уравнений. Однородные уравнения.

Однородные уравнения второй степени. Определение однородного уравнения. Методы решения однородных уравнений. Как понять, что уравнение однородное. Решение однородных уравнений методом замены переменной. Решение уравнений методом замены переменной. Решить уравнение. Решить заменой. Примеры с решением. Задания с объяснением. Алгебра 8 класс.