Как решить уравнение с гиперболой (2 видео)

Гипербола: формулы, примеры решения задач

Содержание

Определение гиперболы, решаем задачи вместе
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Гипербола
Гипербола. График функции и свойства.
теория по математике 📈 функции
Свойства гиперболы (у= k x . )
Построение графика функции
📸 Видео

Видео:Новая задача №9 на гиперболу из ЕГЭ 2022 по математикеСкачать

Определение гиперболы, решаем задачи вместе

Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.

На чертеже ниже фокусы обозначены как и .

На чертеже ветви гиперболы — бордового цвета.

При a = b гипербола называется равносторонней.

Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.

Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.

Точки и , где

называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).

называется эксцентриситетом гиперболы.

Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.

Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.

Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,

Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.

То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.

Подставляем и вычисляем:

Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .

Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:

Если — произвольная точка левой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

Если — произвольная точка правой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

На чертеже расстояния обозначены оранжевыми линиями.

Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).

Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где — расстояние от левого фокуса до точки любой ветви гиперболы, — расстояние от правого фокуса до точки любой ветви гиперболы и и — расстояния этой точки до директрис и .

Пример 4. Дана гипербола . Составить уравнение её директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:

Получаем уравнение директрис гиперболы:

Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.

Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.

Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.

Уравнение гиперболы, отнесённой к асимптотам, имеет вид:

, где .

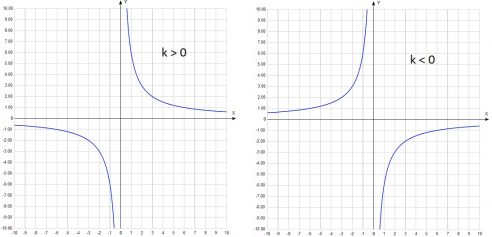
В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.

Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:

Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.

Видео:Видеоурок "Гипербола"Скачать

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) b = 4 , а один из фокусов в точке (5; 0)

2) действительная ось 6, расстояние между фокусами 8

3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы

Видео:Гипербола. Функция k/x и её графикСкачать

Гипербола

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

гипербола, где k y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

Дробь (color <frac>) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment

Видео:функция y=k/x и ее график (гипербола) - 8 класс алгебраСкачать

Гипербола. График функции и свойства.

теория по математике 📈 функции

Графиком функции у= k x . . , где k ≠ 0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Свойства гиперболы (у= k x . )

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

Область определения – любое число, кроме нуля.
Область значения – любое число, кроме нуля.
Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у= 10 x . . .

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.

Теперь для построения гиперболы соединим точки плавной линией. 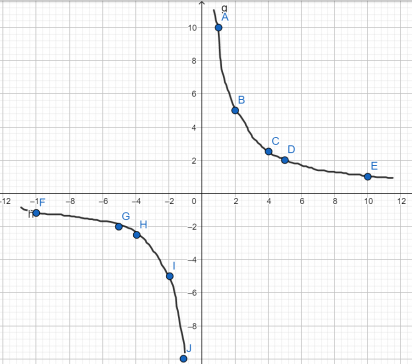Построить график функции у= − 5 x . . .

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

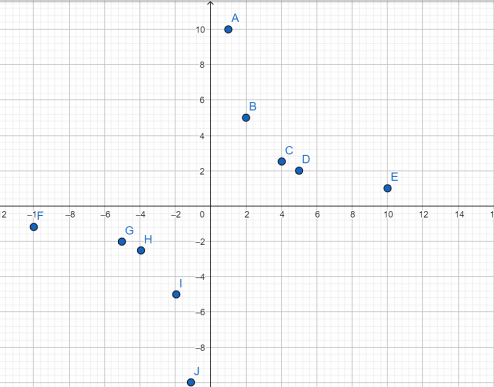
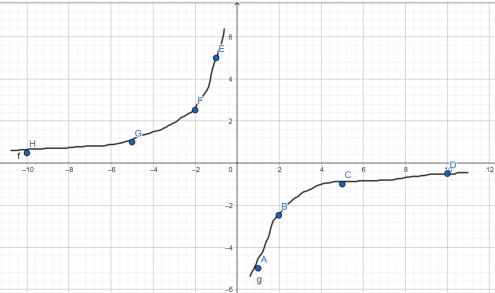
Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

Для решения данной задачи необходимо знать

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

pазбирался: Даниил Романович | обсудить разбор | оценить