В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0 , 1 , 0 , 01 , 100 , 10 и др.
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
- Основы деления десятичных дробей
- Как разделить натуральное число на десятичную дробь и наоборот
- Как разделить десятичную дробь на натуральное число столбиком
- Решение уравнений с дробями
- Понятие дроби
- Основные свойства дробей
- Понятие уравнения
- Понятие дробного уравнения
- Как решать уравнения с дробями
- 1. Метод пропорции
- 2. Метод избавления от дробей
- Что еще важно учитывать при решении
- Универсальный алгоритм решения
- Примеры решения дробных уравнений
- Урок математики по теме «Деление дробей в уравнениях»
- 🎥 Видео
Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Разделите 1 , 2 на 0 , 48 .
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
1 , 2 = 12 10 = 6 5
0 , 48 = 48 100 = 12 25 .
Таким образом, нам надо разделить 6 5 на 12 25 . Считаем:
1 , 2 : 0 , 48 = 6 2 : 12 25 = 6 5 · 25 12 = 6 · 25 5 · 12 = 5 2
Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 2 1 2 , а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 5 2 = 2 , 5 . О том, как это сделать, мы уже писали ранее.
Ответ: 1 , 2 : 0 , 48 = 2 , 5 .
Посчитайте, сколько будет 0 , ( 504 ) 0 , 56 .
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
0 , ( 504 ) = 0 , 504 1 — 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111
После этого конечную десятичную дробь также переведем в другой вид: 0 , 56 = 56 100 . Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:
0 , ( 504 ) : 1 , 11 = 56 111 : 56 100 = 56 111 · 100 56 = 100 111
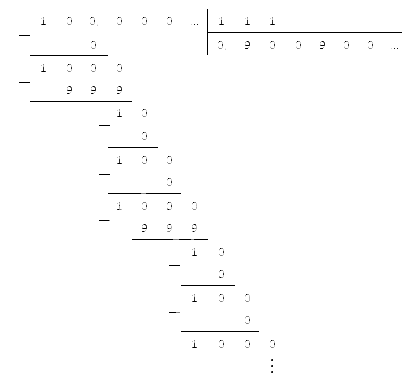
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Ответ: 0 , ( 504 ) : 0 , 56 = 0 , ( 900 ) .
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Найдите, сколько будет 0 , 779 … / 1 , 5602 .
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Можем продолжить подсчеты и получить примерный результат: 0 , 779 … : 1 , 5602 ≈ 0 , 78 : 1 , 56 = 78 100 : 156 100 = 78 100 · 100 156 = 78 156 = 1 2 = 0 , 5 .
Точность результата будет зависеть от степени округления.
Ответ: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .
Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Разделите 2 , 5 на 45 .
Решение
Приведем 2 , 5 к виду обыкновенной дроби: 255 10 = 51 2 . Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:
25 , 5 : 45 = 51 2 : 45 = 51 2 · 1 45 = 17 30
Если перевести результат в десятичную запись, то мы получим 0 , 5 ( 6 ) .
Ответ: 25 , 5 : 45 = 0 , 5 ( 6 ) .
Видео:Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Вычислите, сколько будет 65 , 14 4 .
Решение
Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65 , 1400 , которая будет равна исходной. Теперь пишем столбик для деления на 4 :
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Ответ: 65 , 14 : 4 = 16 , 285 .
Видео:Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).Скачать

Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Видео:ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Видео:Уравнение на десятичные дроби со скобками и делением. Номер 391г.Скачать

Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Видео:КАК РЕШИТЬ УРАВНЕНИЕ С ДЕСЯТИЧНЫМИ ДРОБЯМИ? Примеры | МАТЕМАТИКА 5 классСкачать

Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Видео:Уравнение. 5 класс.Скачать

Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
- Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Видео:«Деление десятичных дробей» #math #умскул_профильнаяматематика #mathematics #аделияадамоваСкачать

Урок математики по теме «Деление дробей в уравнениях»
Разделы: Математика
Форма урока: объяснение нового материала.
Цели урока:
- Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
- Воспитательная: воспитывать самостоятельность, аккуратность
- Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.
Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.
Этапы урока
Слайды
I. Организационный этап
– Здравствуйте, мы проведем сегодня урок по теме «Деление дробей в уравнених». Откройте тетради, запишите число, классная работа и тему урока.
Целью нашего урока является закрепление и проверка умений умножать и делить обыкновенные дроби, а также повторить навыки решения задач и уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)
– Повторим правило деления двух дробей: Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)
– Чтобы решить уравнение необходимо определить какой компонент в уравнении является неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель, что нужно сделать?
– Чтобы найти неизвестный множитель необходимо произведение разделить на известный множитель.
– Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать задачи.
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день? (неизвестно)
– Сколько километров прошел во второй день? (неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:
1)
1)
2) 
3) 
4) 
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех которые не решали в классе.
🎥 Видео
Решение уравнений, 6 классСкачать

Деление десятичной дроби на десятичную дробь. 5 класс.Скачать

Умножение и деление десятичной дроби 😉 Полезный файл в комментарияхСкачать

Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Действия с десятичными дробями 😈Скачать

Деление десятичных дробей в столбик - примеры. Как делить в столбик десятичные дроби?Скачать

УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 классСкачать

Деление числа на десятичную дробь. Математика 5 класс.Скачать


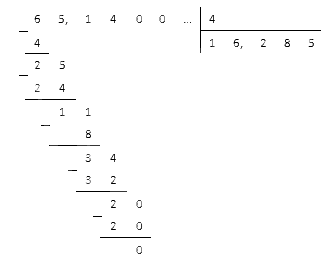



















 1)
1) 






