Как решить уравнение разность кубов (3 видео)

Разность кубов: формула и примеры

В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, разложение разности кубов на множители. Также разберем примеры решения задач для закрепления представленного материала.

Содержание

Формула разности кубов
Доказательство формулы
Примеры задач
Решение кубических уравнений
Решение двучленного кубического уравнения вида A x 3 + B = 0
Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Решение кубических уравнений с рациональными корнями
Решение кубических уравнений по формуле Кардано
Иррациональные уравнения с кубическими радикалами
💥 Видео

Видео:Сумма и разность кубов двух выражений. 7 класс.Скачать

Формула разности кубов

Разность кубов чисел/выражений равняется произведению их разности на неполный квадрат их суммы.

a 3 – b 3 = (a – b)(a 2 + ab + b 2 )

Полный квадрат суммы выглядит следующим образом: (a + b) 2 = a 2 + 2ab + b 2 . В нашем случае во второй скобке напротив второго слагаемого нет множителя 2, поэтому выражение является неполным.

Формула верна и в обратную сторону:

(a – b)(a 2 + ab + b 2 ) = a 3 – b 3

Примечание: a 3 – b 3 ≠ (a – b) 3

Видео:Алгебра 7 класс (Урок№30 - Сумма кубов. Разность кубов.)Скачать

Доказательство формулы

Достаточно просто умножить скобку (a – b) на (a 2 + ab + b 2 ) , чтобы убедиться в том, что выражение верно, т.е. пойти от обратного:

(a – b)(a 2 + ab + b 2 ) = a 3 + a 2 b + ab 2 – a 2 b – ab 2 – b 3 = a 3 – b 3 .

Видео:Куб суммы и куб разности двух выражений. 7 класс.Скачать

Примеры задач

Задание 1
Представьте в виде произведения множителей выражение: (7x) 3 – 5 3 .

Решение
(7x) 3 – 5 3 = (7x – 5)((7x) 2 + 7x ⋅ 5 + 5 2 ) = (7x – 5)(49x 2 + 35x + 25)

Задание 2
Представьте выражение 512x 3 – 27y 3 в виде разности кубов и разложите его на множители.

Решение
512x 3 – 27y 3 = ((8x) 3 – (3y) 3 ) = (8x – 3y)((8x) 2 + 8x ⋅ 3y + (3y) 2 ) = (8x – 3y)(64x 2 + 24xy + 9y 2 )

Видео:Сумма и разность кубов. Алгебра 7 класс. Разложение на множители.Скачать

Решение кубических уравнений

Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.

Видео:Сумма и разность кубов двух выражений. Практическая часть. 7 класс.Скачать

Решение двучленного кубического уравнения вида A x 3 + B = 0

Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что

x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0

Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.

Найти корни кубического уравнения 2 x 3 — 3 = 0 .

Решение

Необходимо найти х из уравнения. Запишем:

2 x 3 — 3 = 0 x 3 — 3 2 = 0

Необходимо применить формулу сокращенного умножения. Тогда получим, что

x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0

Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.

Ответ: x = 3 3 2 6 .

Видео:Сумма и разность кубов двух выражений - 7 класс алгебраСкачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0

Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что

A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A

Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.

Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .

Решение

Уравнение является возвратным. Необходимо произвести группировку. Получим, что

5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0

Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :

5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10

Ответ:

x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1

Видео:Разность квадратов двух выражений. 7 класс.Скачать

Решение кубических уравнений с рациональными корнями

Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .

Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .

Решение

3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0

Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что

D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.

Ответ: х = 0 .

Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :

A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2

Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.

Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .

Решение

Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что

2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0

Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:

± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36

Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида

1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0

Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .

Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:

x i	Коэффициенты многочлена
2	— 11	12	9
— 0 . 5	2	— 11 + 2 · ( — 0 . 5 ) = — 12	12 — 12 · ( — 0 . 5 ) = 18	9 + 18 · ( — 0 . 5 ) = 0

2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9

После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.

Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .

Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.

Видео:7 класс, 24 урок, Формулы сокращённого умноженияСкачать

Решение кубических уравнений по формуле Кардано

Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .

После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .

Полученные p и q в формулу Кардано. Получим, что

y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3

Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.

Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .

Решение

Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .

Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .

Отсюда следует, что

p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108

Производим подстановку в формулу Кордано и получим

y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3

— 343 216 3 имеет три значения. Рассмотрим их ниже.

— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2

Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2

Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6

Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2

Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .

Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .

Преобразуем при помощи формулы Кордано:

y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6

x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3

Ответ: x 1 = — 1 2 , x 2 , 3 = 3

При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.

Видео:Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать

Иррациональные уравнения с кубическими радикалами

Разделы: Математика

Тема: «Иррациональные уравнения вида , .»

(Методическая разработка.)

Основные понятия

Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня (радикала) или знаком возведения в дробную степень.

Уравнение вида f(x)=g(x), где хотя бы одно из выражений f(x) или g(x) иррационально является иррациональным уравнением.

Основные свойства радикалов:

Все радикалы четной степени являются арифметическими, т.е. если подкоренное выражение отрицательно, то радикал не имеет смысла (не существует); если подкоренное выражение равно нулю, то радикал тоже равен нулю; если подкоренное выражение положительно, то значение радикала существует и положительно.
Все радикалы нечетной степени определены при любом значении подкоренного выражения. При этом радикал отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если покоренное выражение положительно.

Методы решения иррациональных уравнений

Решить иррациональное уравнение – значит найти все действительные значения переменной, при подстановке которых в исходное уравнение оно обращается в верное числовое равенство, либо доказать, что таких значений не существует. Иррациональные уравнения решаются на множестве действительных чисел R.

Областью допустимых значений уравнения состоит из тех значений переменной, при которых неотрицательны все выражения, стоящие под знаком радикалов четной степени.

Основными методами решения иррациональных уравнений являются:

а) метод возведения обеих частей уравнения в одну и ту же степень;

б) метод введения новых переменных (метод замен);

в) искусственные приемы решения иррациональных уравнений.

В данной статье остановимся на рассмотрении уравнений определённого выше вида и приведём 6 методов решения таких уравнений.

1 метод. Возведение в куб.

Этот способ требует применения формул сокращённого умножения и не содержит «подводных» камней, т.е. не приводит к появлению посторонних корней.

Пример 1. Решить уравнение

Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению ,

Пример 2. Решить уравнение .

Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению

и рассмотрим полученное уравнение как квадратное относительно одного из корней

следовательно, дискриминант равен 0,а уравнение может иметь решение х=-2.

Проверка:

Замечание: Проверка может быть опущена, в том случае, если дорешивается квадратное уравнение.

2 метод. Возведение в куб по формуле.

По-прежнему будем возводить уравнение в куб, но при этом пользоваться модифицированными формулами сокращенного умножения.

(незначительная модификация известной формулы), тогда

Пример3. Решить уравнение .

Возведём уравнение в куб с использованием формул, приведённых выше.

Но выражение должно быть равно правой части. Поэтому имеем:

, откуда

Теперь при возведении в куб получаем обычное квадратное уравнение:

, и два его корня

Оба значения, как показывает проверка, правильные.

Но все ли преобразования здесь равносильны? Прежде чем ответить на этот вопрос, решим ещё одно уравнение.

Пример4. Решить уравнение .

Возводя, как и ранее, обе части в третью степень, имеем:

Откуда (учитывая, что выражение в скобках равно ), получаем:

, значит

. Получаем, .Сделаем проверку и убедимся х=0 –посторонний корень.

Ответ: .

Ответим на вопрос: «Почему возникли посторонние корни?»

Равенство влечёт равенство . Заменим с на –с, получим:

и .

Нетрудно проверить тождество

Итак, если , то либо , либо . Уравнение можно представить в виде , .

Заменяя с на –с, получаем: если , то либо , либо

Поэтому при использовании этого метода решения обязательно нужно сделать проверку и убедиться что посторонних корней нет.

3 метод. Метод системы.

Пример 5. Решить уравнение .

Введём замену, составим и решим систему уравнений.

Пусть , . Тогда:

откуда очевидно, что

Второе уравнение системы получается таким образом, чтобы линейная комбинация подкоренных выражений не зависела от исходной переменной.

Легко убедиться , что система не имеет решения, следовательно и исходное уравнение не имеет решения.

Ответ: Корней нет.

Пример 6. Решить уравнение .

Введём замену, составим и решим систему уравнений.

Пусть , . Тогда

или

Возвращаясь к исходной переменной имеем:

х=0.

4 метод. Использование монотонности функций.

Прежде чем использовать данный метод обратимся к теории.

Нам понадобятся следующие свойства:

Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, то функция y=f(x)+g(x) также возрастает (убывает ) на этом множестве.
Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, при чем обе они принимают неотрицательные значения при всех допустимых х, то функция y=f(x)g(x) возрастает (убывает) на данном множестве.
Если функция y=f(x) монотонная, то уравнение f(x)=a имеет не более одного решения.
Если функции y=f(x) и y=g(x) имеют разный характер монотонности, то уравнение f(x)=g(x) имеет не более одного решения.
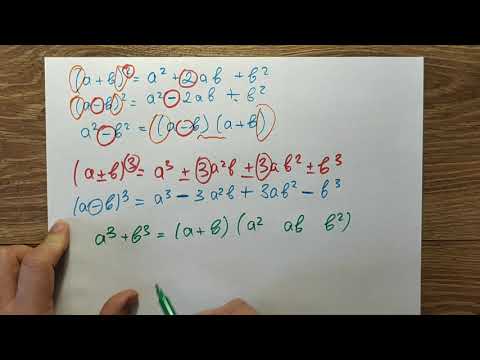
Функция вида возрастает при к>0 и убывает при к 30.05.2009