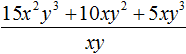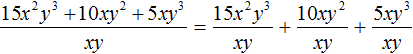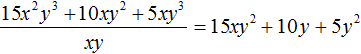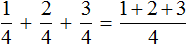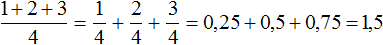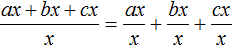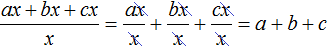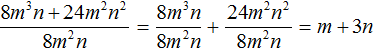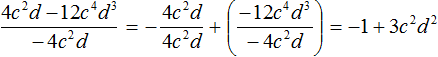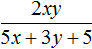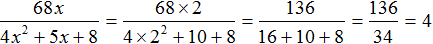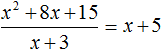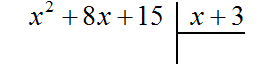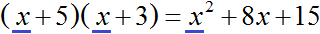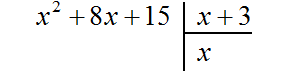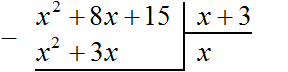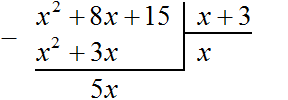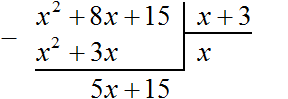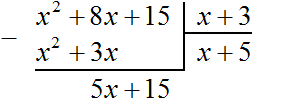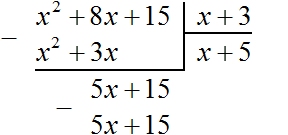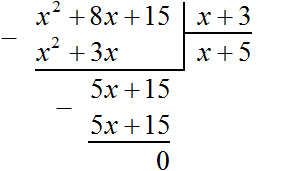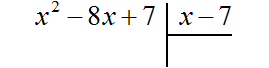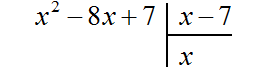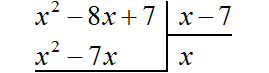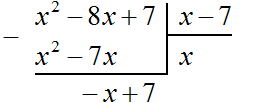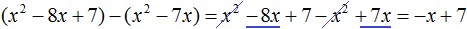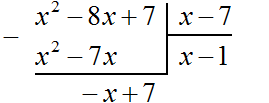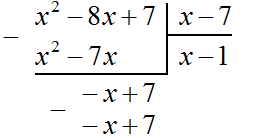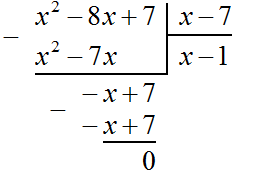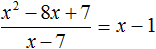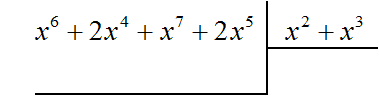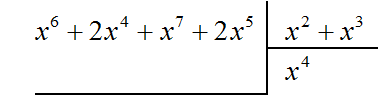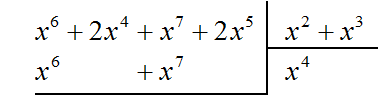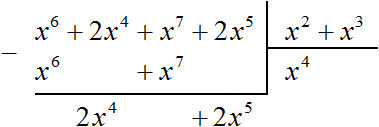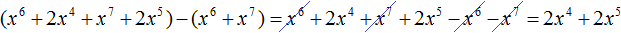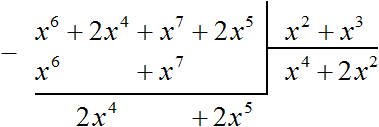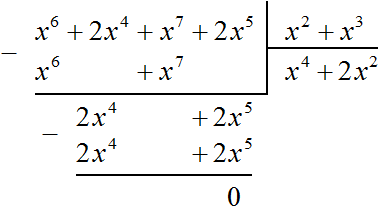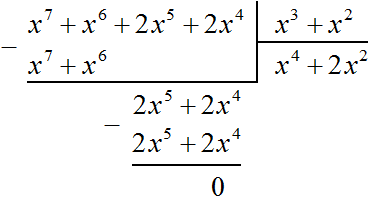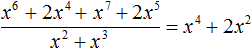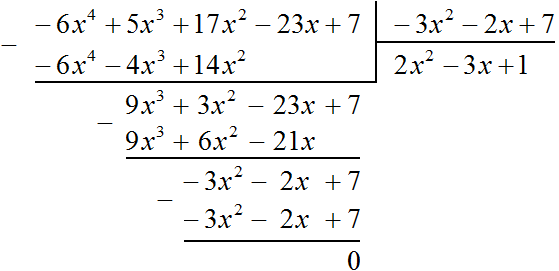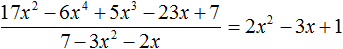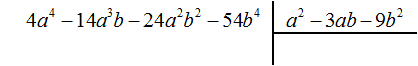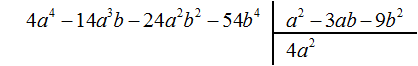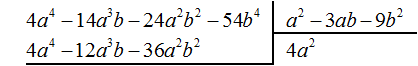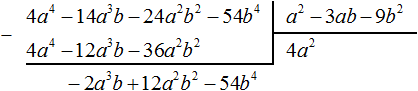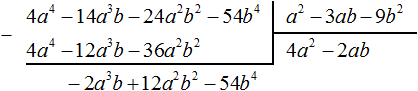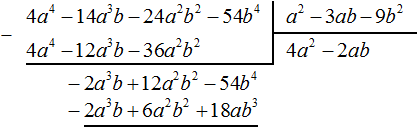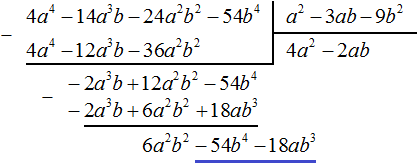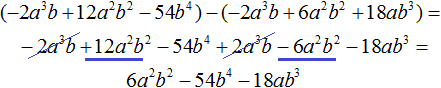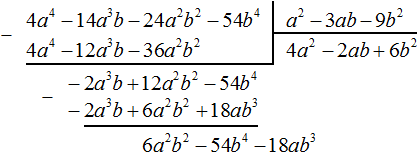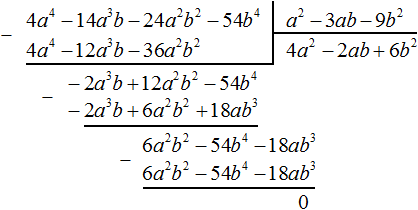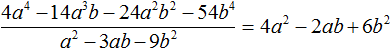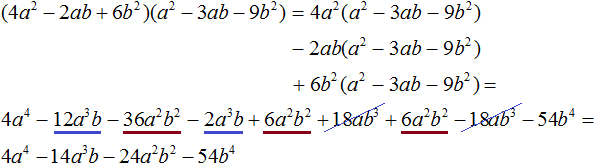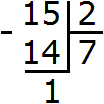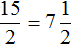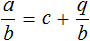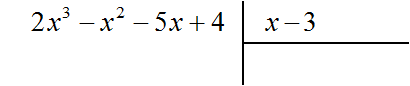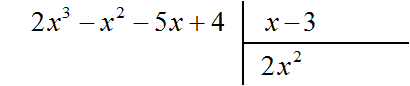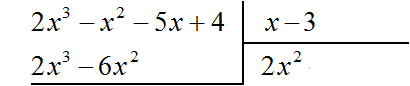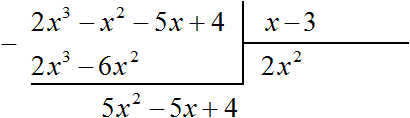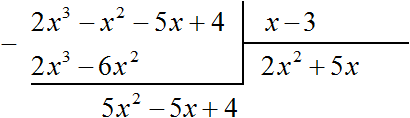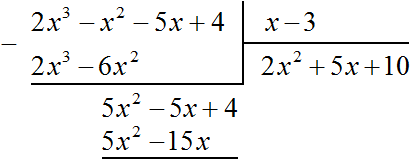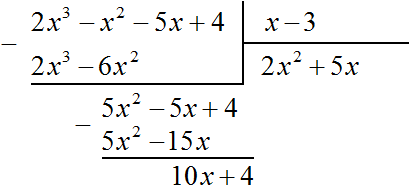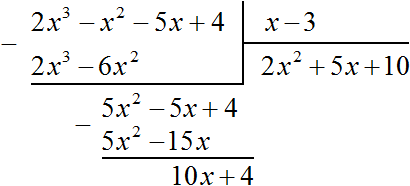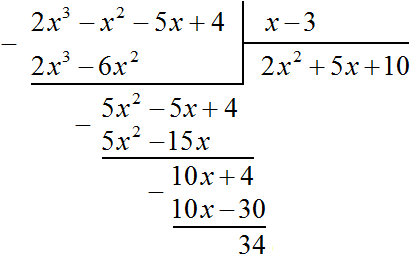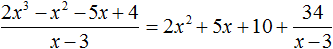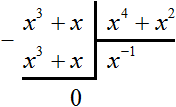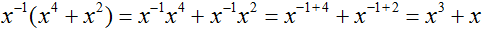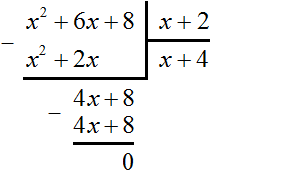Разделы: Математика
Класс: 9
Учебная:
Развивающая:
- Развитие внимания учащихся.
- Развитие умения добиваться результатов труда.
- Развитие интереса к изучению алгебры и навыков самостоятельной работы.
Воспитывающая:
Оборудование: компьютер, проектор.
1 этап работы. Организационный момент.
2 этап работы. Мотивация и выход на постановку проблемы
Уравнение 
В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.
А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.
1) Решение линейного уравнения.
Линейным называется уравнение вида 


2) Решение квадратного уравнения.
Квадратным называется уравнение вида 







Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение 

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена 
3) Решение кубического уравнения.
Решим кубическое уравнение
Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:
Итак, данное кубическое уравнение имеет три корня: 


4) Решение биквадратного уравнения.
Очень распространены биквадратные уравнения, которые имеют вид 


Решим биквадратное уравнение 
Введём новую переменную 


Вернёмся к старой переменной 






Итак, данное биквадратное уравнение имеет четыре корня:



Попробуем решить уравнение 
4 этап работы. Привести некоторые утверждения о корнях многочлена вида 

Приведём некоторые утверждения о корнях многочлена вида 
1) Многочлен 


2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.
3) Если на концах отрезка 


4) Если число 








5) Если уравнение 



5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.
Пример 1. Решим уравнение 
Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: 




Таким образом, мы фактически разложили левую часть уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:
Итак, данное уравнение имеет три корня:
Пример 2. Решим уравнение 
Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: 

Значит, многочлен 



Таким образом, мы разложили левую часть уравнения на множители:
Аналогичным образом поступим и с многочленом 
Если это уравнение 


Значит, многочлен 
произведения 


Таким образом, мы разложили левую часть исходного уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:
Итак, данное уравнение имеет четыре корня:
6 этап работы. Закрепление изученного материала.
Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.
7 этап работы. Вывод урока.
Решить уравнения высших степеней можно следующим образом:
- используя формулы для нахождения корней (если они известны);
- используя замену переменной;
- раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.
8 этап работы. Домашнее задание.
Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).
Видео:Деление многочленов | Математика | TutorOnlineСкачать

Решение уравнения с помощью понижения степени. Деление многочлена на многочлен столбиком
Деление многочлена на многочлен столбиком
Для решения уравнение вида Р(х)=0, где Р(х) — многочлен степени n>2, часто применяют метод понижения степени. Он основывается на таком факте: если число x=b является корнем многочлена P(x), то есть P(b)=0, то многочлен P(x) делится без остатка на двучлен x-b.
После того, как мы разделим многочлен P(x) степени n на двучлен x-b, то мы получим многочлен степени n-1, то есть на единицу меньшей исходного. И дальше процедуру можно повторить.
Если старший коэффициент многочлена P(x) равен 1, то корни многочлена P(x) мы ищем среди делителей свободного члена.
Решим уравнение
Свободный член многочлена в левой части уравнения равен 10.
Делители числа 10: 1; 2; 5; 10.
Проверим, является ли какое-либо из этих чисел корнем многочлена. Для этого последовательно подставим эти значения вместо х в многочлен.




Разделим многочлен 
Видео:Деление многочлена на многочленСкачать

Деление многочленов
Продолжаем изучать многочлены. В данном уроке мы научимся их делить.
Видео:Деление многочлена на многочлен. 10 класс.Скачать

Деление многочлена на одночлен
Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x 2 y 3 + 10xy 2 + 5xy 3 на одночлен xy . Запишем это деление в виде дроби:
Теперь делим каждый член многочлена 15x 2 y 3 + 10xy 2 + 5xy 3 на одночлен xy. Получающиеся частные будем складывать:
Получили привычное для нас деление одночленов. Выполним это деление:
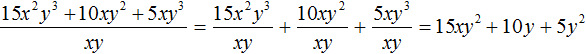
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В нашем примере произведение полученного многочлена 15xy 2 + 10y + 5y 2 и делителя xy должно быть равно многочлену 15x 2 y 3 + 10xy 2 + 5xy 3 , то есть исходному делимому. Проверим так ли это:
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Например, чтобы сложить дроби 

Если мы вычислим выражение 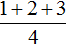

При этом выражение 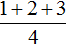
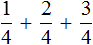
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x , образуется три дроби с общим знаменателем x
Вычисление каждой дроби даст в результате многочлен a + b + c
Пример 2. Разделить многочлен 8m 3 n + 24m 2 n 2 на одночлен 8m 2 n
Пример 3. Разделить многочлен 4c 2 d − 12c 4 d 3 на одночлен −4c 2 d
Видео:✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

Деление одночлена на многочлен
Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.
Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5 .
Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy . Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy , поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.
Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.
Например, найдём значение выражения 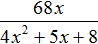
Выражение 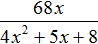
Видео:Схема Горнера. 10 класс.Скачать

Деление многочлена на многочлен
Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3 , получается многочлен x 2 + 8x + 15
Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x 2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5 .
Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Выполним уголком деление многочлена x 2 + 8x + 15 на многочлен x + 3 . Так мы поэтапно увидим, как получается многочлен x + 5 .
В данном случае результат нам известен заранее. Это будет многочлен x + 5 . Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.
Сейчас наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3 , мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5 .
Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.
Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.
Если первый член делимого (в нашем случае это x 2 ) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3 . На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3 , получается x 2 + 3x . Записываем этот многочлен под делимым x 2 + 8x+ 15 так, чтобы подобные члены располагались друг под другом:
Теперь из делимого x 2 + 8x + 15 вычитаем x 2 + 3x . Подобные члены вычитаем из подобных им членов. Если из x 2 вычесть x 2 , получится 0 . Ноль не записываем. Далее если из 8x вычесть 3x , получится 5x . Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
Теперь делим многочлен 5x + 15 на x + 3 . Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x ) разделить на первый член делителя (это член x ). Если 5x разделить на x , получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
Теперь умножаем 5 на делитель x + 3 . При умножении 5 на x + 3 , получается 5x + 15 . Записываем этот многочлен под делимым 5x + 15
Теперь из делимого 5x + 15 вычитаем 5x + 15 . Если из 5x + 15 вычесть 5x + 15 получится 0.
На этом деление завершено.
После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3 , должен получаться многочлен x 2 + 8x + 15
Пример 2. Разделить многочлен x 2 − 8x + 7 на многочлен x − 7
Записываем уголком данное деление:
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x . Записываем x под правым углом:
Умножаем x на x − 7 , получаем x 2 − 7x . Записываем этот многочлен под делимым x 2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Вычитаем из x 2 − 8x + 7 многочлен x 2 − 7x . При вычитании x 2 из x 2 получается 0 . Ноль не записываем. А при вычитании −7x из −8x получается −x , поскольку −8x − (−7x) = −8x + 7x = −x . Записываем −x под членами −7x и −8x . Далее сносим следующий член 7
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:
Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7 . Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x ) разделить на первый член делителя (это член x ). Если −x разделить на x , получится −1 . Записываем −1 под правым углом вместе со своим знаком:
Умножаем −1 на x − 7 , получаем −x + 7 . Записываем этот многочлен под делимым −x + 7
Теперь из −x + 7 вычитаем −x + 7 . Если из −x + 7 вычесть −x + 7 получится 0
Деление завершено. Таким образом, частное от деления многочлена x 2 − 8x + 7 на многочлен x − 7 равно x − 1
Выполним проверку. Умножим частное x − 1 на делитель x − 7 . У нас должен получиться многочлен x 2 − 8x + 7
Пример 3. Разделить многочлен x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3
Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x 4
Умножаем x 4 на делитель x 2 + x 3 и полученный результат записываем под делимым. Если x 4 умножить на x 2 + x 3 получится x 6 + x 7 . Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
Теперь из делимого вычитаем многочлен x 6 + x 7 . Вычитание x 6 из x 6 даст в результате 0. Вычитание x 7 из x 7 тоже даст в результате 0. Оставшиеся члены 2x 4 и 2x 5 снесём:
Получилось новое делимое 2x 4 + 2x 5 . Это же делимое можно было получить, выписав отдельно многочлен x 6 + 2x 4 + x 7 + 2x 5 и вычтя из него многочлен x 6 + x 7
Разделим многочлен 2x 4 + 2x 5 на делитель x 2 + x 3 . Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x 2 . Записываем этот член в частном:
Умножаем 2x 2 на делитель x 2 + x 3 и полученный результат записываем под делимым. Если 2x 2 умножить на x 2 + x 3 получится 2x 4 + 2x 5 . Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
Вычитание многочлена 2x 4 + 2x 5 из многочлена 2x 4 + 2x 5 дало в результате 0, поэтому деление успешно завершилось.
В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.
Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.
Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x 6 + 2x 4 + x 7 + 2x 5 упорядочить в порядке убывания степеней, то получим многочлен x 7 + x 6 + 2x 5 + 2x 4 . А если члены многочлена x 2 + x 3 упорядочить в порядке убывания степеней, то получим многочлен x 3 + x 2
Тогда деление уголком многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 примет следующий вид:
Деление завершено. Таким образом, частное от деления многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 равно x 4 + 2x 2
Выполним проверку. Умножим частное x 4 + 2x 2 на делитель x 2 + x 3 . У нас должен получиться многочлен x 6 + 2x 4 + x 7 + 2x 5
При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Перепишем умножение (x 4 + 2x 2 )(x 2 + x 3 ) упорядочив члены многочленов в порядке убывания степеней.
Пример 4. Разделить многочлен 17x 2 − 6x 4 + 5x 3 − 23x + 7 на многочлен 7 − 3x 2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
Пример 5. Разделить многочлен 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4 на многочлен a 2 − 3ab − 9b 2
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a 2 . Записываем 4a 2 в частном:
Умножим 4a 2 на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 4a 4 − 12a 3 b − 36a 2 b 2
Теперь делим −2a 3 b + 12a 2 b 2 − 54b 4 на делитель a 2 − 3ab − 9b 2 . Разделим первый член делимого на первый член делителя, получим −2ab . Записываем −2ab в частном:
Умножим −2ab на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым −2a 3 b + 12a 2 b 2 − 54b 4
Вычтем из многочлена −2a 3 b + 12a 2 b 2 − 54b 4 многочлен −2a 3 b + 12a 2 b 2 − 18ab 3 . При вычитании подобных членов обнаруживаем, что члены −54b 4 и 18ab 3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a 3 b из −2a 3 b и 6a 2 b 2 из 12a 2 b 2 , а вычитание 18ab 3 из −54b 4 запишем в виде разности −54b 4 − (+18ab 3 ) или −54b 4 − 18ab 3
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
Вернёмся к нашей задаче. Разделим 6a 2 b 2 − 54b 4 − 18ab 3 на делитель a 2 − 3ab − 9b 2 . Делим первый член делимого на первый член делителя, получим 6b 2 . Записываем 6b 2 в частном:
Умножим 6b 2 на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым 6a 2 b 2 − 54b 4 − 18ab 3 . Сразу вычтем этот полученный результат из делимого 6a 2 b 2 − 54b 4 − 18ab 3
Деление завершено. Таким образом, частное от деления многочлена 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4 на многочлен a 2 − 3ab − 9b 2 равно 4a 2 − 2ab + 6b 2 .
Выполним проверку. Умножим частное 4a 2 − 2ab + 6b 2 на делитель a 2 − 3ab − 9b 2 . У нас должен получиться многочлен 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4
Видео:Математика без Ху!ни. Деление многочлена на многочлен.Скачать

Деление многочлена на многочлен с остатком
Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
Рациональное число 
Например, если при делении многочлена a на многочлен b получится частное c , да еще останется остаток q , то ответ будет записан так:
Например, разделим многочлен 2x 3 − x 2 − 5x + 4 на многочлен x − 3
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x 2 . Записываем 2x 2 в частном:
Умножим 2x 2 на делитель x − 3 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 2x 3 − 6x 2
Теперь делим 5x 2 − 5x + 4 на делитель x − 3 . Разделим первый член делимого на первый член делителя, получим 5x . Записываем 5x в частном:
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x 2 − 5x + 4
Вычтем из многочлена 5x 2 − 5x + 4 многочлен 5x 2 − 15x
Теперь делим 10x + 4 на делитель x − 3 . Разделим первый член делимого на первый член делителя, получим 10 . Записываем 10 в частном:
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4 . Сразу вычтем этот полученный результат из делимого 10x + 4
Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4 , является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34 .
Поэтому при делении многочлена 2x 3 − 2x 2 − 5x + 4 на многочлен x − 3 получается 2x 2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
Видео:Деление многочленов. Теорема Безу. Объяснение на пальцахСкачать

Когда деление многочленов невозможно
Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.
Например, нельзя разделить многочлен x 3 + x на многочлен x 4 + x 2 , поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.
Вопреки этому запрету можно попробовать разделить многочлен x 3 + x на многочлен x 4 + x 2 , и даже получить частное x − 1 , которое при перемножении с делителем будет давать делимое:
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x − 1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x − 1 это дробь 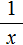
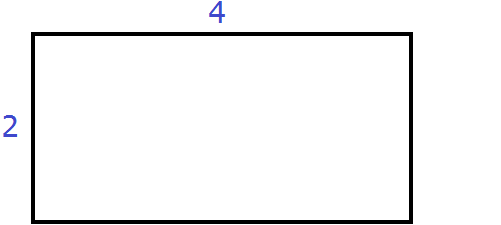
Пусть имеется прямоугольник со сторонами 4 и 2
Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
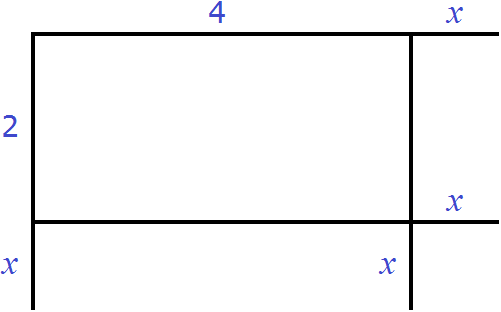
Увеличим длину и ширину этого прямоугольника на x
Достроим отсутствующие стороны:
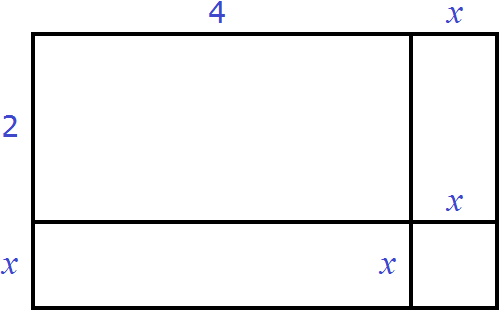
Теперь прямоугольник имеет длину x + 4 и ширину x + 2 . Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x 2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x 2 + 6x + 8 на ширину x + 2 и получить длину x + 4 .
Степень многочлена x 2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2 , а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.
💡 Видео
ЕГЭ по математике. Деление многочлена на двучленСкачать

Схема Горнера. Объяснение на пальцах. Деление многочленовСкачать

Теорема Безу. 10 класс.Скачать

7 класс, 23 урок, Умножение многочлена на многочленСкачать

Деление многочлена на многочлен уголком, в столбикСкачать

Деление многочлена на многочлен. Практическая часть. 10 класс.Скачать

Теорема Безу и разложение многочлена на множителиСкачать

Многочлены: деление, разложение на множители, теорема Безу и теорема о делимости.Скачать

деление многочлена на многочлен :)Скачать

10 кл. Алгебра. 3 четв. Деление многочлена на многочлен "уголком"Скачать

Произведение многочленов. 7 класс.Скачать

Деление многочленов столбиком и схема ГорнераСкачать

нод многочленовСкачать