Как решить уравнение cos2x sin2x 0 75

Условие

а) Решите уравнение cos2x+sin^2x=0,75

б) Найдите все корни этого уравнения, принадлежащие отрезку [− 3π ; − 3π/2].

Решение

cos2x+sin^2x=0,75
cos2x=1-2sin^2x
1-2sin^2x+sin^2x=0,75
sin^2x=1/4
sinx=-1/2 или sinx=1/2

sinx=-1/2
x=- (π/6)+2πk, k∈Z или x= (-5π/6)+2πn, n∈Z

sinx=1/2
x=(π/6)+2πm, m∈Z или x= (5π/6)+2πp, p∈Z

О т в е ты можно записать так
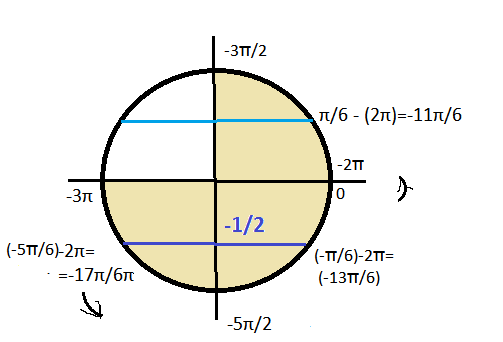
х=± (π/6)+πk, k∈Z или х=± (5π/6)+πk, k∈Z
см. рисунок.
Указанному промежутку принадлежат корни
-17π/6; -13π/6; -11π/6

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Помогите с решением, пожалуйстаРешить уравнение :cos2x + sin ^ 2x = 0, 75Найти все корни этого уравнения, принадлежащие отрезку [π ; 5π / 2] ?

Математика | 10 — 11 классы

Помогите с решением, пожалуйста

cos2x + sin ^ 2x = 0, 75

Найти все корни этого уравнения, принадлежащие отрезку [π ; 5π / 2] .

Начнем с того, что cos2x = cos ^ 2(x) — sin ^ 2(x) и 0.

Видим, что можно сократить sin ^ 2(x), что и проделаем

отсюда$x=arccos(frac<sqrt>)+fracn$, где n пренадлежит Z (множеству целых чисел)

Поскольку рассматриваем только отрезок [π ; 5π / 2], то берем только n при которых решение будет лежать в данном отрезке.

Решим 2 уравнения, с помощью которого найдем удовлетворяющие нас n,

1 уравнение будет иметь вид :

К n является целым числом, нужно округлить получившийся результат до целого числа, округление производится в бОльшую сторону, т.

К. это начало отрезка, получаем n = 2

Здесь округляем в мЕньшую сторону, т.

К это конец отрезка и получаем n = 4.

Ответ : $x=frac+fracn$ где n = 2, 3, 4.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

3) Найти корни уравнения 2 sin x + 1 = 0, принадлежащие отрезку [0 ; 2пи]?

3) Найти корни уравнения 2 sin x + 1 = 0, принадлежащие отрезку [0 ; 2пи].

Видео:ЕГЭ профиль 13 задание Тригонометрическое уравнение cos2x-0,25+sin^2 x=0Скачать

ПОМОГИТЕ РЕШИТЬ СРОЧНО ПОЖАЛУЙСТА а)cos2x = sin(x — ) б) и а) б) найти сумму корней принадлежащий отрезку ()?

ПОМОГИТЕ РЕШИТЬ СРОЧНО ПОЖАЛУЙСТА а)cos2x = sin(x — ) б) и а) б) найти сумму корней принадлежащий отрезку ().

Видео:КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать

Найдите все решения уравнения cos 2x + sin ^ 2x = cos x?

Найдите все решения уравнения cos 2x + sin ^ 2x = cos x.

Укажите корни , принадлежащие отрезку[ — п ; п].

Видео:Решите уравнение ➜ sin⁡x+cos⁡x=1 ➜ 2 способа решенияСкачать

Найти все корни уравнения (36 ^ cosx) ^ sinx = (1 / 6) ^ sqrt2 * sinx, принадлежащие отрезку [ — п ; п / 2]?

Найти все корни уравнения (36 ^ cosx) ^ sinx = (1 / 6) ^ sqrt2 * sinx, принадлежащие отрезку [ — п ; п / 2].

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

А) Решите уравнение (27 ^ cosx) ^ sinx = 3 ^ 3cosx / 3 б) Найдите все корни этого уравнения , принадлежащие отрезку [ — 7пи / 2 ; — 5пи / 2]?

А) Решите уравнение (27 ^ cosx) ^ sinx = 3 ^ 3cosx / 3 б) Найдите все корни этого уравнения , принадлежащие отрезку [ — 7пи / 2 ; — 5пи / 2].

Видео:Как решать тригонометрическое уравнение 3cos^2x-sinx-1=0 Замена sinx=t Уравнение с косинусом и синусСкачать

Помогите, пожалуйста?

Решить уравнение : 2sin(7пи / 2 — х) * sinx = cosx и наити все корни, принадлежащие отрезку от 7пи / 2 до 5пи.

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Решите уравнение 2sin ^ 2x — cosx — 1 = 0?

Решите уравнение 2sin ^ 2x — cosx — 1 = 0.

Укажите корни , принадлежащие отрезку(3пи , 4пи).

Видео:Как решать тригонометрические неравенства?Скачать

А) Решите уравнение sin2x + 2sinx = 3√cosx + 3√?

А) Решите уравнение sin2x + 2sinx = 3√cosx + 3√.

Б) Укажите корни этого уравнения, принадлежащие отрезку [− 3π ; −3π2].

Видео:Решение уравнения a*sin^2(x)+b*sin(x)*cos(x)+c*cos^2(x)=0Скачать

Решите уравнение : 0, 5sin2x + sin ^ 2x — sinx = cosx Найдите все корни этого уравнения, принадлежащие промежутку [ — 2п ; — п / 2]?

Решите уравнение : 0, 5sin2x + sin ^ 2x — sinx = cosx Найдите все корни этого уравнения, принадлежащие промежутку [ — 2п ; — п / 2].

Видео:Как решать тригонометрическое уравнение cos^2 x =1/2 Уравнение с косинусом в квадрате Решите уравненСкачать

Решите уравнение : 2cos ^ 3x — cos ^ 2x — cosx = 0 Найдите все корни этого уравнения, принадлежащие отрезку [ — 2П ; — П] Уравнение решил, но определить корни на отрезке не могу?

Решите уравнение : 2cos ^ 3x — cos ^ 2x — cosx = 0 Найдите все корни этого уравнения, принадлежащие отрезку [ — 2П ; — П] Уравнение решил, но определить корни на отрезке не могу.

Можно поподробнее показать как это делать.

Если вам необходимо получить ответ на вопрос Помогите с решением, пожалуйстаРешить уравнение :cos2x + sin ^ 2x = 0, 75Найти все корни этого уравнения, принадлежащие отрезку [π ; 5π / 2] ?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Будет 46, т. К если стоит число равное или большее 5, то округляем. Меньше — не округляем.

2 / 3×3 / 5 сокращаем тройки и получаем : 2×1 / 5 = 2 / 5 ; 2 / 5×10 = 20 / 5 = 4.

Рисунок а ВО ОD OC АD АО АС BD рисунок б МК МN MP NP KP KN EK EF EN ES KF SN.

А) отрезки : АО, АD, АС, ВО, ВD, ОС, ОD б) отрезки : МК, МN, MP, KN, NP, KP, FK, FE, KE, SE, SN, NE.

Поскольку задание очень неточное и малопонятное, то сначала создадим общую папку и файл в ней, а потом скачаем ее с другого компьютера. Алгоритм для ОС Windows 10 Создадим общую папку1) Одинаково называем рабочую группу у обоих компьютеров. Пуск → ..

1)(80 * х + 24) : 180 = 4 80х + 24 = 180 : 4 80х + 24 = 45 80х = 45 — 24 80х = 21 х = 3, 8 2)500 — 360 * (у — 4) = 160 360 * (у — 4) = 500 — 160 360 * (у — 4) = 340 у — 4 = 340 : 360 у — 4 = 0, 9 у = 4, 9.

Длина прямоугольника = 2, 4 см 2, 4 : 3 * 2 = 1, 6 ширина периметр = 2 * 2, 4 + 2 * 1, 6 = 4, 8 + 3, 2 = 8см площадь = 2, 4 * 1, 6 = 3, 84.

6 отрезков. AB, AC, AD, BC, BD, CD.

AB, AC, AD, AC, AD, BC, CD.

1)16 см ; 20 см 2)36 кг : 40 кг 3)18л ; 18л 4)8дм ; 6дм 5)3м ; 4м 6)6 мин ; 2мин.

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Тригонометрические уравнения sin2x=√2/2; cos x/3=-1/2Скачать

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение

Видео:Урок №2. Решение тригонометрических уравнений. Задание №13 ЕГЭ по математике профильного уровняСкачать

Немного теории.

Видео:How to Solve cos(x) + sin(2x) = 0 (Trigonometric Equations)Скачать

Тригонометрические уравнения

Видео:Решите уравнение ★ cos⁡x+sin⁡x=1 ★ Как решать простые уравнения?Скачать

Уравнение cos(х) = а

Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если a

Видео:4 способа решить уравнение sinx = cosxСкачать

Уравнение sin(х) = а

Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac; ; frac right] ) имеет только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если а

Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале ( left( -frac; ; frac right) ) только один корень. Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right) ); если а

Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Видео:Простые уравнения. Как решать простые уравнения?Скачать

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text(0,5) + pi n = (-1)^n frac + pi n, ; n in mathbb )
Ответ ( x = (-1)^n frac + pi n, ; n in mathbb )

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) — 2 = 0

Используя формулы ( sin(x) = 2sinfrac cosfrac, ; cos(x) = cos^2 frac -sin^2 frac ) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac + cos^2 frac right) ) получаем

Поделив это уравнение на ( cos^2 frac ) получим равносильное уравнение ( 3 text^2frac — 4 textfrac +1 = 0 )
Обозначая ( textfrac = y ) получаем уравнение 3y 2 — 4y + 1 = 0, откуда y₁=1, y₁= 1/3

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0