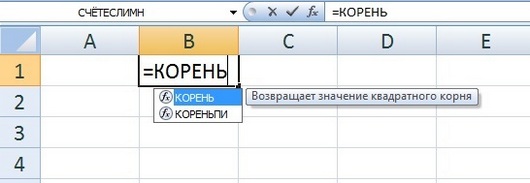
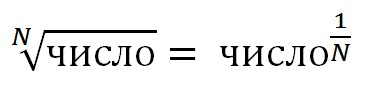На клавиатуре нет кнопок с написанием квадратного или другого корня, поэтому в Excel создана специальная функция, вводит и вычисляет квадратный корень. Как ей воспользоваться, а также как извлечь корни разных степеней в Excel? Рассмотрим несколько примеров.
Важно! Функции в Excel вводятся в ячейках русскими буквами без пробелов, перед названием функции ставится знак равно =
За квадратный корень отвечает функция КОРЕНЬ(значение). Чтобы воспользоваться ей, нужно в ячейке написать =КОРЕНЬ и без пробелов внутри скобки написать значение, от которого нужно найти квадратный корень.
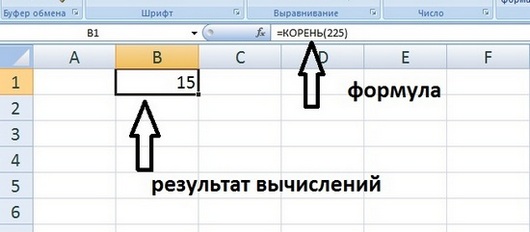
- =КОРЕНЬ(225) — квадратный корень от числа 225;
- =КОРЕНЬ(А1) — квадратный корень от значения ячейки А1;
- =КОРЕНЬ(10+G6) — квадратный корень от суммы 10 и значения ячейки G6;
- Как извлечь в Excel корень третьей, четвертой и иной степеней?
- Решение уравнений в excel — примеры решений
- Первый метод
- Второй метод
- Третий метод
- Четвертый метод
- Решение уравнений в Excel методом итераций Крамера и Гаусса
- Решение уравнений методом подбора параметров Excel
- Как решить систему уравнений матричным методом в Excel
- Решение системы уравнений методом Крамера в Excel
- Решение систем уравнений методом Гаусса в Excel
- Примеры решения уравнений методом итераций в Excel
- 💡 Видео
Видео:Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

Как извлечь в Excel корень третьей, четвертой и иной степеней?
Для квадратного корня есть своя функция — КОРЕНЬ — а как быть с другими с другими корнями?
Из курса математики известно, что извлечение корня N —степени равно возведению числа в степень 1/ N .
- извлечение квадратного корня (второй степени) соответствует возведению в степень 1/2;
- кубического (третьей степени) — в 1/3;
- четвертой степени — в 1/4 и т.д.
Этой формулой и нужно пользоваться для вычисления корней разных степеней в Excel. Для возведения степени использовать функцию СТЕПЕНЬ(аргумент) или галочку ^ (на английской раскладке SHIFT + 6). Саму дробную степень писать в скобках.
- =27^(1/3) — извлечение кубического корня из числа 27;
- =D3^(1/4) — извлечение корня четвертой степени из значения ячейки D3;
- =(F2+15)^(1/5) — извлечение корня пятой степени из суммы значения ячейки F2 и числа 15.
- =(A1^2+(D1+3)^5)^(1/3) — выражение для
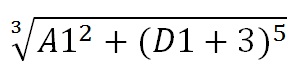
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.
Кстати, такая возможность есть
на всех страницах нашего сайта
| | 2007-2022 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU». Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов. Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.
О работе с сайтом Мы используем cookie. Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами. При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах. Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены. Видео:Уравнение четвертой степениСкачать  Решение уравнений в excel — примеры решенийMicrosoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel. Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать  Первый методСуть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если». 1. Зададимся простым квадратичным уравнением и найдем решение при х=0. 2. Переходите к инструменту и заполняете все необходимые поля 3. После проведения вычислений программа выдаст результат в ячейке с иксом. 4. Подставив полученное значение в исходное уравнение можно проверить правильность решения. Видео:Математика | Кубические уравнения по методу СталлонеСкачать  Второй методИспользуем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной. 1. Создаете два диапазона.
2. Переходите во вкладку Вставка и выбираете обычный график. 3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах. Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных. Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать  Третий методРешение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее. 1. Записываете произвольную систему уравнений. 2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно. 3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter. 4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш. Видео:9 класс. Алгебра. Решение уравнений четвертой степени. Возвратные уравнения.Скачать  Четвертый методМетодом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив. 2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66). Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter. 3. Маркером автозаполнения копируете формулу в нижнюю строку. 4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения. 5. Повторяете операцию для третьей строки, используя формулу =C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена. 6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78 7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77 8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76 9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении. Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных. Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных. Жми «Нравится» и получай только лучшие посты в Facebook ↓ Видео:8 класс. Алгебра. Решение уравнений четвертой степени.Скачать  Решение уравнений в Excel методом итераций Крамера и ГауссаВ программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами. Рассмотрим на примерах некоторые варианты решений. Видео:Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать  Решение уравнений методом подбора параметров ExcelИнструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог. Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра». Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления». Видео:Решение уравнений с помощью ExcelСкачать  Как решить систему уравнений матричным методом в ExcelДана система уравнений:
Получены корни уравнений. Видео:Уравнение четвертой степени (Метод Феррари)Скачать  Решение системы уравнений методом Крамера в ExcelВозьмем систему уравнений из предыдущего примера: Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В. Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей. Рассчитаем также определитель матрицы А (массив – диапазон матрицы А). Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|). Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений: Видео:Решение уравнений четвертой степени. Идея метода ФеррариСкачать  Решение систем уравнений методом Гаусса в ExcelДля примера возьмем простейшую систему уравнений: 3а + 2в – 5с = -1 Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В. Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
Видео:Как решать возвратные уравнения?Скачать  Примеры решения уравнений методом итераций в ExcelВычисления в книге должны быть настроены следующим образом: Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула: M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления: f’ (1) = -2 * f’ (2) = -11. Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11. В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)). В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1. Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат: 💡 ВидеоExcel Подбор параметра. Решение математических уравненийСкачать  УДИВИТЕЛЬНЫЙ способ решения уравнения 4-ой степениСкачать  Решение уравнения в Excel. Используется средство "Подбор параметра"Скачать  Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать  Решение уравнения третьей степени x³-9x-12=0Скачать  КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать  Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать  Уравнение 4-й степени. Метод ФеррариСкачать  |